| This article is about the mathematical definition of interpolation. For other uses, see Interpolation (disambiguation). |
Interpolation is a means of determining an approximate value at an arbitrary point for a continuous function between two or more known points. The known points are used to determine the coefficients of a fitting function, which is then used to calculate the value at the unknown point. The nature of the fitting function determines the order of accuracy, as well as the required number of known points. Some fitting functions include:
| Polynomial Interpolation | ||
| Name | Function | Points required |
| 0th order (nearest value) |
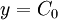 |
1 |
| 1st order (linear) |
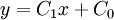 |
2 |
| 2nd order (parabollic) |
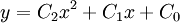 |
3 |
| 3rd order (cubic) |
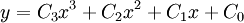 |
4 |
| nth order | 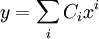 |
i + 1 |
| Trigonometric Interpolation | ||
| 1st order | 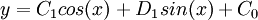 |
3 |
| nth order | 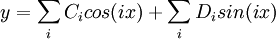 |
2i + 1 |
- A constant (nearest value interpolation);
- A straight line (linear interpolation);
- A parabola (parabolic interpolation); and
- A cubic function (cubic interpolation).
Interpolation can take place spatially, as well as temporally. In the finite volume method, spatial interpolation between control volume centres and face centres is frequently used during the discretization process. Interpolation is denoted:
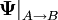
Where:
-
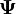 is the variable undergoing interpolation;
is the variable undergoing interpolation;
- A and B are the locations before and after interpolation respecitvely, and can be:
- c for volume centres;
- f for face centres;
- p for nodal points;
- told for the previous time step;
- tnew for the next time step; or
- any other spatial or temporal designation.