Difference between revisions of "ChemFoam"
(→Evolution of the pressure) |
(→Evolution of the pressure) |
||
| Line 194: | Line 194: | ||
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
| − | <center><math> | + | <center><math>_ |
| − | p = \sum p_i | + | p = \sum p_i = \sum n_i \frac{R T}{V} = \sum \frac{m_i}{M_i} \frac{R T}{V} = \sum \frac{y_i}{M_i} \underbrace{ \frac{m_{tot}}{V}}_{\rho_0} R T |
</math></center> | </math></center> | ||
</td><td width="5%">(x)</td></tr></table> | </td><td width="5%">(x)</td></tr></table> | ||
Revision as of 13:14, 24 January 2020
chemFoam
Solver for chemistry problems, designed for use on single cell cases to provide comparison against other chemistry solvers, that uses a single cell mesh, and fields created from the initial conditions.
Contents
1 Solution Strategy
This solver provides an excellent starting point for those who want to have a first impression on the influence of the chemical reactions in the equations describing the evolution of the species concentration and also the evolution of temperature (i.e. the energy equation). Since the computational domain consists only of one cell, the only mechanism influencing the evolution of the spices concentration and of the temperature are the chemical reactions. The system of equations which is solved is the following:
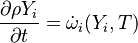 | (1) |
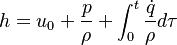 | (2) |
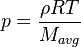 | (3) |
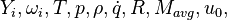 are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
Like most of the solvers present in OpenFOAM also this solver follows a segregated solution strategy. That means that for each quantity of interest one linear equation is solved and the coupling between the equations is achieved by explicit source terms. Briefly summarized the solution is achieved as follows:
1) Solve the chemistry: The purpose is to get the reaction rates for each species involved and the heat realized by the chemical reaction
2) Solve the species equation: The purpose it to get the species concentration at the new time step
3) Solve the energy equation: Here we get the enthalpy (over the thermodynamics also the temperature) at the new time step
4) Solve the pressure equation: Required to calculate the enthalpy
The source code can be found in chemFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | Copyright (C) 2010-2011 OpenCFD Ltd. \\/ M anipulation | ------------------------------------------------------------------------------- | Copyright (C) 2011-2017 OpenFOAM Foundation ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application chemFoam Group grpCombustionSolvers Description Solver for chemistry problems, designed for use on single cell cases to provide comparison against other chemistry solvers, that uses a single cell mesh, and fields created from the initial conditions. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "psiReactionThermo.H" #include "BasicChemistryModel.H" #include "reactingMixture.H" #include "chemistrySolver.H" #include "OFstream.H" #include "thermoPhysicsTypes.H" #include "basicSpecieMixture.H" #include "hexCellFvMesh.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Solver for chemistry problems, designed for use on single cell cases" " to provide comparison against other chemistry solvers" ); argList::noParallel(); #define CREATE_MESH createSingleCellMesh.H #define NO_CONTROL #include "postProcess.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createSingleCellMesh.H" #include "createFields.H" #include "createFieldRefs.H" #include "readInitialConditions.H" #include "createControls.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (runTime.run()) { #include "readControls.H" #include "setDeltaT.H" ++runTime; Info<< "Time = " << runTime.timeName() << nl << endl; #include "solveChemistry.H" #include "YEqn.H" #include "hEqn.H" #include "pEqn.H" #include "output.H" runTime.printExecutionTime(Info); } Info << "Number of steps = " << runTime.timeIndex() << endl; Info << "End" << nl << endl; return 0; } // ************************************************************************* //
2 Chemical reactions
Elementary chemical reaction involving  species in
species in  reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
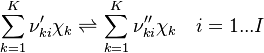 | (4) |
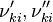 and
and 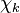 are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie
are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie 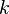 , respectively.
, respectively.
In order to make the notation more clear to those who start learning about the usage of CFD to simulate combustion process, Zel'dovich mechanism for the oxidation of N0 (see https://en.wikipedia.org/wiki/Zeldovich_mechanism or also the book of [2]) is used as an example:
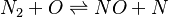 |
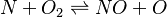 |
Based on the above example the forward 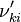 , the backward stoichiometric coefficient
, the backward stoichiometric coefficient 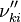 and the chemical symbol of the specie k
and the chemical symbol of the specie k 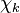 can be written as follows:
can be written as follows:
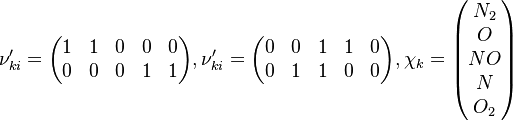 3 Evolution of species4 Evolution of energy5 Evolution of the pressureIn order to calculate the pressure Daltons model is used: It says that the thermodynamic pressure can be calculated as the sum of the partial pressures of the individual species (see e.g. https://en.wikipedia.org/wiki/Dalton%27s_law):
{ rho = thermo.rho(); if (constProp == "volume") { scalar invW = 0.0; forAll(Y, i) { invW += Y[i][0]/specieData[i].W(); } Rspecific[0] = 1000.0*constant::physicoChemical::R.value()*invW; p[0] = rho0*Rspecific[0]*thermo.T()[0]; rho[0] = rho0; } } 6 References |