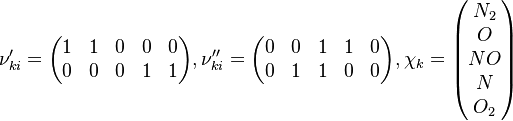
The reactions are specified in the file constant/thermophysicalProperties where the chemistry reader, the file containing the reactions and the thermodynamic properties have to be specified:
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: v1912 |
| \\ / A nd | Website: www.openfoam.com |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "constant";
object thermophysicalProperties;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
thermoType
{
type hePsiThermo;
mixture reactingMixture;
transport sutherland;
thermo janaf;
energy sensibleEnthalpy;
equationOfState perfectGas;
specie specie;
}
chemistryReader foamChemistryReader;
foamChemistryFile "<constant>/reactions";
foamChemistryThermoFile "<constant>/thermo";
//CHEMKINFile "<case>/chemkin/chem.inp";
//CHEMKINThermoFile "<case>/chemkin/therm.dat";
//CHEMKINTransportFile "<case>/chemkin/transportProperties";
// ************************************************************************* //
For the above example the reactions look as follows:
elements 2(O N);
species 5(O O2 N2 N NO);
reactions
{
un-named-reaction-0
{
type reversibleArrheniusReaction;
reaction "NO^1 + N^1 = N2^1 + O^1";
A 2.1e+10;
beta 0;
Ta 0;
}
un-named-reaction-1
{
type reversibleArrheniusReaction;
reaction "N^1 + O2^1 = NO^1 + O^1";
A 5.83e+06;
beta 1.01;
Ta 3120;
}
}
In our example both reactions are reversible Arrhenius reactions. A is the per-exponent factor, Ta the activation temperature and beta is the exponent of the temperature in the calculation of the reaction rate (see below for further explanations). The values are taken from the book of [3]. Note that the values of the constants are calculated in the OpenFOAM native unit system of kmol, m3, s, K.
2.2 Chemical reaction rate
Having established the chemical reactions which are desired to be solved, the next step is to describe the velocity at which the chemical reaction occur, i.e. the change of the concentration of the single species with time. The reaction rate 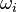 of the reaction i can be written as (see also the book [4]): of the reaction i can be written as (see also the book [4]):
![\omega_i = k_{fi} \prod_k [X]_k^{\nu_{ki}'} - k_{ri} \prod_k [X]_k^{\nu_{ki}''}](/images/math/0/8/b/08b53dce9957da556577c563ae8cc9d4.png)
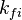 and and 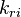 are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients 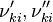 are used. However the user can explicitly set it by adding the hat sign ^ after the chemical symbol (see also https://openfoamwiki.net/images/8/8a/Christ_OFW6_slides.pdf). are used. However the user can explicitly set it by adding the hat sign ^ after the chemical symbol (see also https://openfoamwiki.net/images/8/8a/Christ_OFW6_slides.pdf). ![[X]_k](/images/math/c/b/c/cbc7d65a80a572c296064e8d44295626.png) is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written: is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
![\omega_1 = k_{f1}[NO][N] - k_{r1}[N2][O]](/images/math/a/7/0/a70bab94d73fb8ba6a8d65ebeb62aa68.png)
![\omega_2 = k_{f2}[N][O2] - k_{r2}[NO][O]](/images/math/2/2/c/22c6c68a7dd5ad6b945b412d1fe801a7.png)
The calculation of the reaction rates of each reaction is done in the function omega of the file $FOAM_SRC/thermophysicalModels/chemistryModel/chemistryModel/StandardChemistryModel/StandardChemistryModel.C:
template<class ReactionThermo, class ThermoType>
Foam::scalar Foam::StandardChemistryModel<ReactionThermo, ThermoType>::omega
(
const Reaction<ThermoType>& R,
const scalarField& c,
const scalar T,
const scalar p,
scalar& pf,
scalar& cf,
label& lRef,
scalar& pr,
scalar& cr,
label& rRef
) const
{
const scalar kf = R.kf(p, T, c);
const scalar kr = R.kr(kf, p, T, c);
pf = 1.0;
pr = 1.0;
const label Nl = R.lhs().size();
const label Nr = R.rhs().size();
label slRef = 0;
lRef = R.lhs()[slRef].index;
pf = kf;
for (label s = 1; s < Nl; s++)
{
const label si = R.lhs()[s].index;
if (c[si] < c[lRef])
{
const scalar exp = R.lhs()[slRef].exponent;
pf *= pow(max(c[lRef], 0.0), exp);
lRef = si;
slRef = s;
}
else
{
const scalar exp = R.lhs()[s].exponent;
pf *= pow(max(c[si], 0.0), exp);
}
}
cf = max(c[lRef], 0.0);
{
const scalar exp = R.lhs()[slRef].exponent;
if (exp < 1.0)
{
if (cf > SMALL)
{
pf *= pow(cf, exp - 1.0);
}
else
{
pf = 0.0;
}
}
else
{
pf *= pow(cf, exp - 1.0);
}
}
label srRef = 0;
rRef = R.rhs()[srRef].index;
// Find the matrix element and element position for the rhs
pr = kr;
for (label s = 1; s < Nr; s++)
{
const label si = R.rhs()[s].index;
if (c[si] < c[rRef])
{
const scalar exp = R.rhs()[srRef].exponent;
pr *= pow(max(c[rRef], 0.0), exp);
rRef = si;
srRef = s;
}
else
{
const scalar exp = R.rhs()[s].exponent;
pr *= pow(max(c[si], 0.0), exp);
}
}
cr = max(c[rRef], 0.0);
{
const scalar exp = R.rhs()[srRef].exponent;
if (exp < 1.0)
{
if (cr>SMALL)
{
pr *= pow(cr, exp - 1.0);
}
else
{
pr = 0.0;
}
}
else
{
pr *= pow(cr, exp - 1.0);
}
}
return pf*cf - pr*cr;
}
In order to get the reaction rate of the spices k, the reaction rates of each reaction containing the species k has to be multiplied with the stoichiometric coefficient and summed with a positive sign if the species is a product in with a negative sign if the species is a reactant (see also e.g. https://en.wikipedia.org/wiki/Reaction_rate).
It can be written as (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf and the books cited here):
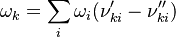
For our example reaction we get:
![\omega_k = \frac{d [X_k]}{dt} = \begin{pmatrix}\frac{d[N_2]}{dt} \\ \frac{d[O]}{dt} \\ \frac{d[NO]}{dt} \\ \frac{d[N]}{dt} \\ \frac{d[O_2]}{dt} \\\end{pmatrix} = \begin{pmatrix} -\omega_1 \\ -\omega_1 + \omega_2 \\ \omega_1 + \omega_2 \\ \omega_1 - \omega_2 \\ \omega_2 \\\end{pmatrix} = \begin{pmatrix} -(k_{f1}[NO][N] - k_{r1}[N2][O]) \\ -(k_{f1}[NO][N] - k_{r1}[N2][O]) + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] - (k_{f2}[N][O2] - k_{r2}[NO][O]) \\ k_{f2}[N][O2] - k_{r2}[NO][O] \\\end{pmatrix}](/images/math/5/4/0/540092492d5d478241d0558e87b6766c.png)
Looking at the above equation we see that the equation describing the evolution of the species concentration is a coupled non--linear differential equation. The calculation of the reaction rates of each species is done in the function of the file $FOAM_SRC/thermophysicalModels/chemistryModel/chemistryModel/StandardChemistryModel/StandardChemistryModel.C:
template<class ReactionThermo, class ThermoType>
void Foam::StandardChemistryModel<ReactionThermo, ThermoType>::omega
(
const scalarField& c,
const scalar T,
const scalar p,
scalarField& dcdt
) const
{
scalar pf, cf, pr, cr;
label lRef, rRef;
dcdt = Zero;
forAll(reactions_, i)
{
const Reaction<ThermoType>& R = reactions_[i];
scalar omegai = omega
(
R, c, T, p, pf, cf, lRef, pr, cr, rRef
);
forAll(R.lhs(), s)
{
const label si = R.lhs()[s].index;
const scalar sl = R.lhs()[s].stoichCoeff;
dcdt[si] -= sl*omegai;
}
forAll(R.rhs(), s)
{
const label si = R.rhs()[s].index;
const scalar sr = R.rhs()[s].stoichCoeff;
dcdt[si] += sr*omegai;
}
}
}
2.3 Chemical reaction rate constants
The remaining two quantities to define are the forward and backward reaction rate constants 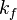 and and 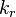 . .
2.3.1 Forward rate constants
The forward rate constant is calculated for Arrhenius type reactions as follows (see also [5]):
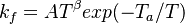
A is the per-exponent factor, Ta the activation temperature and beta is the exponent of the temperature in the calculation of the reaction rate. The soure code can be find in $FOAM_SRC/thermophysicalModels/specie/reaction/reactionRate/ArrheniusReactionRate/ArrheniusReactionRateI.H:
inline Foam::scalar Foam::ArrheniusReactionRate::operator()
(
const scalar p,
const scalar T,
const scalarField&
) const
{
scalar ak = A_;
if (mag(beta_) > VSMALL)
{
ak *= pow(T, beta_);
}
if (mag(Ta_) > VSMALL)
{
ak *= exp(-Ta_/T);
}
return ak;
}
2.3.2 Reverse rate constants
The reverse rate of the ith reaction is calculated as follows (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf) :
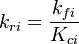
The equilibrium constant is calculated as follows:
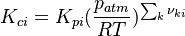
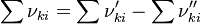 is the sum of the stoichiometric coefficient of the ith reaction. Furthermore is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
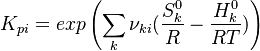
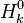 and and 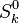 are the molar enthalpy and entropy of the species k . are the molar enthalpy and entropy of the species k .
The reverse rate constant is calculated in the file $FOAM_SRC/thermophysicalModels/specie/reaction/Reactions/ReversibleReaction/ReversibleReaction.C:
template
<
template<class> class ReactionType,
class ReactionThermo,
class ReactionRate
>
Foam::scalar Foam::ReversibleReaction
<
ReactionType,
ReactionThermo,
ReactionRate
>::kr
(
const scalar kfwd,
const scalar p,
const scalar T,
const scalarField& c
) const
{
return kfwd/max(this->Kc(p, T), 1e-6);
}
The calculation of Kc can be found in the file $FOAM_SRC/thermophysicalModels/specie/thermo/thermo/thermoI.H.
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::K(const scalar p, const scalar T) const
{
scalar arg = -this->Y()*this->G(Pstd, T)/(RR*T);
if (arg < 600)
{
return exp(arg);
}
else
{
return VGREAT;
}
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Kp(const scalar p, const scalar T) const
{
return K(p, T);
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Kc(const scalar p, const scalar T) const
{
const scalar nm = this->Y()/this->W();
if (equal(nm, SMALL))
{
return Kp(p, T);
}
else
{
return Kp(p, T)*pow(Pstd/(RR*T), nm);
}
}
It is not so easily seen how the sum of the stoichiometric coefficients enters the calculation of the equilibrium constant. For this reason it is explained in a bit more detail (see also the thread https://www.cfd-online.com/Forums/openfoam/224970-understanding-reverse-rate-calculation-chemical-reactions.html). In order to calculate the equilibrium constant for each reaction a pseudo mixture is set where the thermodynamic properties of the mixture are weighted with the stoichiometric coefficient. This is done in the constructor of the Reaction object by calling the function setThermo:
template<class ReactionThermo>
Foam::Reaction<ReactionThermo>::Reaction
(
const speciesTable& species,
const List<specieCoeffs>& lhs,
const List<specieCoeffs>& rhs,
const HashPtrTable<ReactionThermo>& thermoDatabase,
bool initReactionThermo
)
:
ReactionThermo::thermoType(*thermoDatabase[species[0]]),
name_("un-named-reaction-" + Foam::name(getNewReactionID())),
species_(species),
lhs_(lhs),
rhs_(rhs)
{
if (initReactionThermo)
{
setThermo(thermoDatabase);
}
}
template<class ReactionThermo>
void Foam::Reaction<ReactionThermo>::setThermo
(
const HashPtrTable<ReactionThermo>& thermoDatabase
)
{
typename ReactionThermo::thermoType rhsThermo
(
rhs_[0].stoichCoeff
*(*thermoDatabase[species_[rhs_[0].index]]).W()
*(*thermoDatabase[species_[rhs_[0].index]])
);
for (label i=1; i<rhs_.size(); ++i)
{
rhsThermo +=
rhs_[i].stoichCoeff
*(*thermoDatabase[species_[rhs_[i].index]]).W()
*(*thermoDatabase[species_[rhs_[i].index]]);
}
typename ReactionThermo::thermoType lhsThermo
(
lhs_[0].stoichCoeff
*(*thermoDatabase[species_[lhs_[0].index]]).W()
*(*thermoDatabase[species_[lhs_[0].index]])
);
for (label i=1; i<lhs_.size(); ++i)
{
lhsThermo +=
lhs_[i].stoichCoeff
*(*thermoDatabase[species_[lhs_[i].index]]).W()
*(*thermoDatabase[species_[lhs_[i].index]]);
}
ReactionThermo::thermoType::operator=(lhsThermo == rhsThermo);
}
To undestand how the equilibrium constant Kc is calcualted we have to have a look at the operators +=, * and == defined in the thermodynamic packages. In the above listing a spieces is constructed where the thermodynimc properties are first multiplied with the stoichiometric coefficient and the molare weight, then the sum of the spieces at the right and left hand side of the chemical reaction is performed and as last step the == operator is applied. As an illustrative example to explain this operations we take the constant properties termodynamic package. The conclusions drawn here can be applied to all other packages as well.
template<class EquationOfState>
inline Foam::hConstThermo<EquationOfState> Foam::operator*
(
const scalar s,
const hConstThermo<EquationOfState>& ct
)
{
return hConstThermo<EquationOfState>
(
s*static_cast<const EquationOfState&>(ct),
ct.Cp_,
ct.Hf_
);
}
template<class EquationOfState>
inline void Foam::hConstThermo<EquationOfState>::operator+=
(
const hConstThermo<EquationOfState>& ct
)
{
scalar Y1 = this->Y();
EquationOfState::operator+=(ct);
if (mag(this->Y()) > SMALL)
{
Y1 /= this->Y();
scalar Y2 = ct.Y()/this->Y();
Cp_ = Y1*Cp_ + Y2*ct.Cp_;
Hf_ = Y1*Hf_ + Y2*ct.Hf_;
}
}
template<class EquationOfState>
inline Foam::hConstThermo<EquationOfState> Foam::operator==
(
const hConstThermo<EquationOfState>& ct1,
const hConstThermo<EquationOfState>& ct2
)
{
EquationOfState eofs
(
static_cast<const EquationOfState&>(ct1)
== static_cast<const EquationOfState&>(ct2)
);
return hConstThermo<EquationOfState>
(
eofs,
ct2.Y()/eofs.Y()*ct2.Cp_
- ct1.Y()/eofs.Y()*ct1.Cp_,
ct2.Y()/eofs.Y()*ct2.Hf_
- ct1.Y()/eofs.Y()*ct1.Hf_
);
}
The first operator analized the * operator. When a hConstThermo object is muliplied with a scalar s the operator returns a new object very only the equationOfState attribute is muliplied by this scalar. For this reason we have to look at the operator * in the equationOfState object. As an axemple we look at the perfectGas equation of state:
template<class Specie>
inline Foam::perfectGas<Specie> Foam::operator*
(
const scalar s,
const perfectGas<Specie>& pg
)
{
return perfectGas<Specie>(s*static_cast<const Specie&>(pg));
}
It returns a perfectGas object were the Specie attribut is muliplied with this scalar. For the Specie attribut the * operator returns a specie with the Y_ attribute multiplied by the scalar s:
inline specie operator*(const scalar s, const specie& st)
{
return specie
(
s*st.Y_,
st.molWeight_
);
}
So the application of the operator leads only to a change of the Y_ attribute in both the left and right hand side of the chemical reaction:
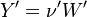
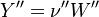
The next operator we're going to examine is the += operator. We see that first the Y_ attribute is stored to the variable Y1. Than the += operator of the equation of state is executed. After that the weighted sum of the thermodynamic properties of the two involved species is taken.
template<class Specie>
inline void Foam::perfectGas<Specie>::operator+=(const perfectGas<Specie>& pg)
{
Specie::operator+=(pg);
}
inline void specie::operator+=(const specie& st)
{
const scalar sumY = Y_ + st.Y_;
if (mag(sumY) > SMALL)
{
molWeight_ = sumY/(Y_/molWeight_ + st.Y_/st.molWeight_);
}
Y_ = sumY;
}
It's easyly seen, that for the attributes Y and molWeight we obtain for the left hand side and right hand side of the chemical equation:
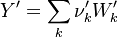
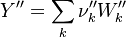
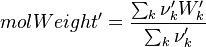
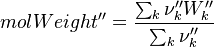
For the thermodynamic properties Hf (chemical enthalpy) and the specific heat capacity we get:
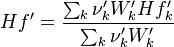
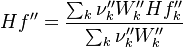
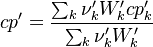
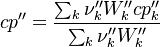
The final operator we have a look is the == operator. Also here first the equation of state == operator is executed. Also as for the other operators the equation of state == operator executes the == of the species:
template<class Specie>
inline Foam::perfectGas<Specie> Foam::operator==
(
const perfectGas<Specie>& pg1,
const perfectGas<Specie>& pg2
)
{
return perfectGas<Specie>
(
static_cast<const Specie&>(pg1) == static_cast<const Specie&>(pg2)
);
}
inline specie operator==(const specie& st1, const specie& st2)
{
scalar diffY = st2.Y_ - st1.Y_;
if (mag(diffY) < SMALL)
{
diffY = SMALL;
}
const scalar diffRW = st2.Y_/st2.molWeight_ - st1.Y_/st1.molWeight_;
#ifdef __clang__
// Using intermediate volatile bool to prevent compiler optimising out the
// if block (above) - CLANG 3.7.1
volatile const bool valid = (mag(diffRW) > SMALL);
const scalar molWeight = valid ? diffY/diffRW : GREAT;
#else
scalar molWeight = GREAT;
if (mag(diffRW) > SMALL)
{
molWeight = diffY/diffRW;
}
#endif
return specie(diffY, molWeight);
}
So after the application of the == we get for the Y and molWeight attribut of the specie:
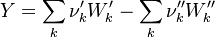
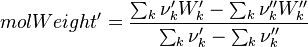
For the thermodynamic properties we get:
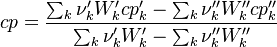
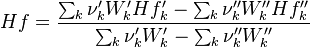
Finnaly if we look how the enthalpy and the entropy are computed for the combination hconst and perfectGas we can veryfy that the same definition for the equilibrium constant 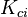 as for chemkin is obtained: as for chemkin is obtained:
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::G(const scalar p, const scalar T) const
{
return this->Ha(p, T) - T*this->S(p, T);
}
template<class EquationOfState>
inline Foam::scalar Foam::hConstThermo<EquationOfState>::Ha
(
const scalar p, const scalar T
) const
{
return Hs(p, T) + Hc();
}
template<class EquationOfState>
inline Foam::scalar Foam::hConstThermo<EquationOfState>::Hs
(
const scalar p, const scalar T
) const
{
return Cp_*T + EquationOfState::H(p, T);
}
template<class EquationOfState>
inline Foam::scalar Foam::hConstThermo<EquationOfState>::Hc() const
{
return Hf_;
}
template<class Specie>
inline Foam::scalar Foam::perfectGas<Specie>::S(scalar p, scalar T) const
{
return -this->R()*log(p/Pstd);
}
template<class Specie>
inline Foam::scalar Foam::perfectGas<Specie>::H(scalar p, scalar T) const
{
return 0;
}
2.4 Heat released by the chemical reactions
3 Evolution of species
{
forAll(Y, specieI)
{
volScalarField& Yi = Y[specieI];
solve
(
fvm::ddt(rho, Yi) - chemistry.RR(specieI),
mesh.solver("Yi")
);
}
}
4 Evolution of energy
The energy equation is derived from the first law of thermodynamics (see also https://en.wikipedia.org/wiki/Enthalpy): For closed systems the change of internal energy is equal to the heat supplied to the system. For open systems the change of enthalpy is equal to the heat supplied to the system. For the first case we get:
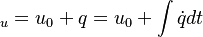
| (x) |
If we add on both sides the pressure divided by the density we get:
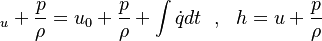
| (x) |
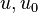 are the internal energy and the internal energy at the time 0. are the internal energy and the internal energy at the time 0.
{
volScalarField& h = thermo.he();
if (constProp == "volume")
{
h[0] = u0 + p[0]/rho[0] + integratedHeat;
}
else
{
h[0] = h0 + integratedHeat;
}
thermo.correct();
}
With the above equation the evolution of the enthalpy with time can be calculated. Knowing the functional dependency of the heat capacity at constant pressure 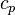 a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here https://caefn.com/openfoam/temperature-calculation. a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here https://caefn.com/openfoam/temperature-calculation.
5 Evolution of the pressure
In order to calculate the pressure Daltons model is used: It says that the thermodynamic pressure can be calculated as the sum of the partial pressures of the individual species (see e.g. https://en.wikipedia.org/wiki/Dalton%27s_law):
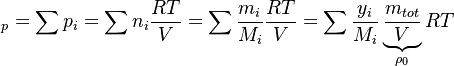
| (x) |
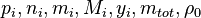 are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively. are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.
{
rho = thermo.rho();
if (constProp == "volume")
{
scalar invW = 0.0;
forAll(Y, i)
{
invW += Y[i][0]/specieData[i].W();
}
Rspecific[0] = 1000.0*constant::physicoChemical::R.value()*invW;
p[0] = rho0*Rspecific[0]*thermo.T()[0];
rho[0] = rho0;
}
}
Note that the constant 1000 in the above code comes from the fact that in OpenFOAM the molar weight is specified in [kg/kmol]. See the file $FOAM_SRC/thermophysicalModels/specie/specie/specie.H.
6 References
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Poinsot, Thierry, and Denis Veynante. Theoretical and numerical combustion. RT Edwards, Inc., 2005.
- ↑ Poinsot, Thierry, and Denis Veynante. Theoretical and numerical combustion. RT Edwards, Inc., 2005.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
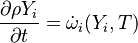
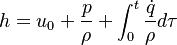
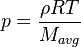
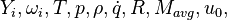 are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
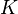 species in
species in 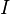 reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
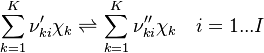
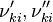 and
and 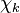 are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie
are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie 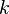 , respectively.
, respectively.
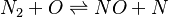
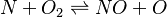
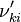 , the backward stoichiometric coefficient
, the backward stoichiometric coefficient 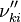 and the chemical symbol of the specie k
and the chemical symbol of the specie k 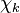 can be written as follows:
can be written as follows:
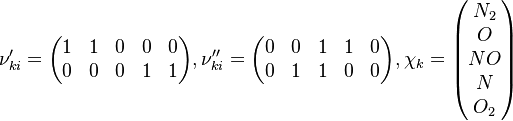
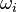 of the reaction i can be written as (see also the book
of the reaction i can be written as (see also the book ![\omega_i = k_{fi} \prod_k [X]_k^{\nu_{ki}'} - k_{ri} \prod_k [X]_k^{\nu_{ki}''}](/images/math/0/8/b/08b53dce9957da556577c563ae8cc9d4.png)
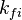 and
and 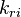 are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients
are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients ![[X]_k](/images/math/c/b/c/cbc7d65a80a572c296064e8d44295626.png) is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
![\omega_1 = k_{f1}[NO][N] - k_{r1}[N2][O]](/images/math/a/7/0/a70bab94d73fb8ba6a8d65ebeb62aa68.png)
![\omega_2 = k_{f2}[N][O2] - k_{r2}[NO][O]](/images/math/2/2/c/22c6c68a7dd5ad6b945b412d1fe801a7.png)
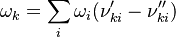
![\omega_k = \frac{d [X_k]}{dt} = \begin{pmatrix}\frac{d[N_2]}{dt} \\ \frac{d[O]}{dt} \\ \frac{d[NO]}{dt} \\ \frac{d[N]}{dt} \\ \frac{d[O_2]}{dt} \\\end{pmatrix} = \begin{pmatrix} -\omega_1 \\ -\omega_1 + \omega_2 \\ \omega_1 + \omega_2 \\ \omega_1 - \omega_2 \\ \omega_2 \\\end{pmatrix} = \begin{pmatrix} -(k_{f1}[NO][N] - k_{r1}[N2][O]) \\ -(k_{f1}[NO][N] - k_{r1}[N2][O]) + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] - (k_{f2}[N][O2] - k_{r2}[NO][O]) \\ k_{f2}[N][O2] - k_{r2}[NO][O] \\\end{pmatrix}](/images/math/5/4/0/540092492d5d478241d0558e87b6766c.png)
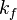 and
and 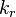 .
.
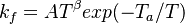
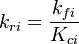
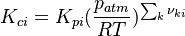
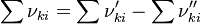 is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
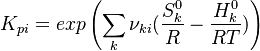
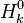 and
and 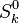 are the molar enthalpy and entropy of the species k .
are the molar enthalpy and entropy of the species k .
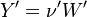
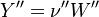
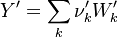
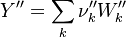
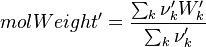
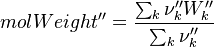
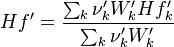
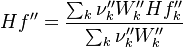
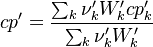
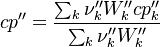
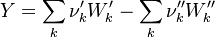
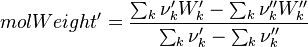
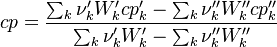
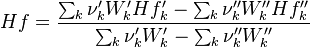
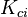 as for chemkin is obtained:
as for chemkin is obtained:
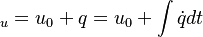
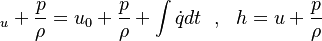
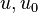 are the internal energy and the internal energy at the time 0.
are the internal energy and the internal energy at the time 0.
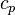 a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here
a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here 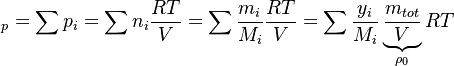
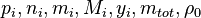 are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.
are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.