chemFoam
Solver for chemistry problems, designed for use on single cell cases to
provide comparison against other chemistry solvers, that uses a single cell
mesh, and fields created from the initial conditions.
1 Solution Strategy
This solver provides an excellent starting point for those who want to have a first impression on the influence of the chemical reactions in the equations describing the evolution of the species concentration and also the evolution of temperature (i.e. the energy equation). Since the computational domain consists only of one cell, the only mechanism influencing the evolution of the spices concentration and of the temperature are the chemical reactions. The system of equations which is solved is the following:
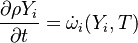
| (1) |
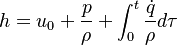
| (2) |
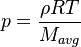
| (3) |
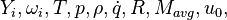 are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
Like most of the solvers present in OpenFOAM also this solver follows a segregated solution strategy. That means that for each quantity of interest one linear equation is solved and the coupling between the equations is achieved by explicit source terms. Briefly summarized the solution is achieved as follows:
1) Solve the chemistry: The purpose is to get the reaction rates for each species involved and the heat realized by the chemical reaction
2) Solve the species equation: The purpose it to get the species concentration at the new time step
3) Solve the energy equation: Here we get the enthalpy (over the thermodynamics also the temperature) at the new time step
4) Solve the pressure equation: Required to calculate the enthalpy
The source code can be found in chemFoam.C
/*---------------------------------------------------------------------------*\
========= |
\\ / F ield | OpenFOAM: The Open Source CFD Toolbox
\\ / O peration |
\\ / A nd | Copyright (C) 2010-2011 OpenCFD Ltd.
\\/ M anipulation |
-------------------------------------------------------------------------------
| Copyright (C) 2011-2017 OpenFOAM Foundation
-------------------------------------------------------------------------------
License
This file is part of OpenFOAM.
OpenFOAM is free software: you can redistribute it and/or modify it
under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
OpenFOAM is distributed in the hope that it will be useful, but WITHOUT
ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License
for more details.
You should have received a copy of the GNU General Public License
along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>.
Application
chemFoam
Group
grpCombustionSolvers
Description
Solver for chemistry problems, designed for use on single cell cases to
provide comparison against other chemistry solvers, that uses a single cell
mesh, and fields created from the initial conditions.
\*---------------------------------------------------------------------------*/
#include "fvCFD.H"
#include "psiReactionThermo.H"
#include "BasicChemistryModel.H"
#include "reactingMixture.H"
#include "chemistrySolver.H"
#include "OFstream.H"
#include "thermoPhysicsTypes.H"
#include "basicSpecieMixture.H"
#include "hexCellFvMesh.H"
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
int main(int argc, char *argv[])
{
argList::addNote
(
"Solver for chemistry problems, designed for use on single cell cases"
" to provide comparison against other chemistry solvers"
);
argList::noParallel();
#define CREATE_MESH createSingleCellMesh.H
#define NO_CONTROL
#include "postProcess.H"
#include "setRootCaseLists.H"
#include "createTime.H"
#include "createSingleCellMesh.H"
#include "createFields.H"
#include "createFieldRefs.H"
#include "readInitialConditions.H"
#include "createControls.H"
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
Info<< "\nStarting time loop\n" << endl;
while (runTime.run())
{
#include "readControls.H"
#include "setDeltaT.H"
++runTime;
Info<< "Time = " << runTime.timeName() << nl << endl;
#include "solveChemistry.H"
#include "YEqn.H"
#include "hEqn.H"
#include "pEqn.H"
#include "output.H"
runTime.printExecutionTime(Info);
}
Info << "Number of steps = " << runTime.timeIndex() << endl;
Info << "End" << nl << endl;
return 0;
}
// ************************************************************************* //
2 Chemical reactions
Elementary chemical reaction involving 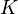 species in
species in 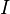 reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
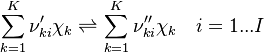
| (4) |
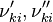 and
and 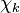 are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie
are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie 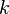 , respectively.
, respectively.
In order to make the notation more clear to those who start learning about the usage of CFD to simulate combustion process, Zel'dovich mechanism for the oxidation of N0 (see https://en.wikipedia.org/wiki/Zeldovich_mechanism or also the book of [2]) is used as an example:
Based on the above example the forward 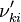 , the backward stoichiometric coefficient
, the backward stoichiometric coefficient 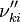 and the chemical symbol of the specie k
and the chemical symbol of the specie k 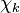 can be written as follows:
can be written as follows:
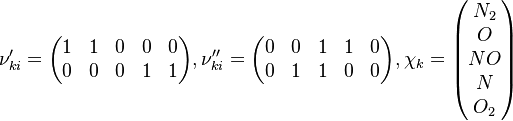
The reactions are specified in the file constant/thermophysicalProperties where the chemistry reader, the file containing the reactions and the thermodynamic properties have to be specified:
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: v1912 |
| \\ / A nd | Website: www.openfoam.com |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "constant";
object thermophysicalProperties;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
thermoType
{
type hePsiThermo;
mixture reactingMixture;
transport sutherland;
thermo janaf;
energy sensibleEnthalpy;
equationOfState perfectGas;
specie specie;
}
chemistryReader foamChemistryReader;
foamChemistryFile "<constant>/reactions";
foamChemistryThermoFile "<constant>/thermo";
//CHEMKINFile "<case>/chemkin/chem.inp";
//CHEMKINThermoFile "<case>/chemkin/therm.dat";
//CHEMKINTransportFile "<case>/chemkin/transportProperties";
// ************************************************************************* //
For the above example the reactions look as follows:
elements 2(O N);
species 5(O O2 N2 N NO);
reactions
{
un-named-reaction-0
{
type reversibleArrheniusReaction;
reaction "NO^1 + N^1 = N2^1 + O^1";
A 2.1e+10;
beta 0;
Ta 0;
}
un-named-reaction-1
{
type reversibleArrheniusReaction;
reaction "N^1 + O2^1 = NO^1 + O^1";
A 5.83e+06;
beta 1.01;
Ta 3120;
}
}
In our example both reactions are reversible Arrhenius reactions. A is the per-exponent factor, Ta the activation temperature and beta is the exponent of the temperature in the calculation of the reaction rate (see below for further explanations). The values are taken from the book of [3]. Note that the values of the constants are calculated in the OpenFOAM native unit system of kmol, m3, s, K.
Having established the chemical reactions which are desired to be solved, the next step is to describe the velocity at which the chemical reaction occur, i.e. the change of the concentration of the single species with time. The reaction rate 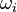 of the reaction i can be written as (see also the book [4]): of the reaction i can be written as (see also the book [4]):
![\omega_i = k_{fi} \prod_k [X]_k^{\nu_{ki}'} - k_{ri} \prod_k [X]_k^{\nu_{ki}''}](/images/math/0/8/b/08b53dce9957da556577c563ae8cc9d4.png)
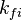 and and 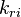 are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients 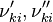 are used. However the user can explicitly set it by adding the hat sign ^ after the chemical symbol (see also https://openfoamwiki.net/images/8/8a/Christ_OFW6_slides.pdf). are used. However the user can explicitly set it by adding the hat sign ^ after the chemical symbol (see also https://openfoamwiki.net/images/8/8a/Christ_OFW6_slides.pdf). ![[X]_k](/images/math/c/b/c/cbc7d65a80a572c296064e8d44295626.png) is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written: is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
![\omega_1 = k_{f1}[NO][N] - k_{r1}[N2][O]](/images/math/a/7/0/a70bab94d73fb8ba6a8d65ebeb62aa68.png)
![\omega_2 = k_{f2}[N][O2] - k_{r2}[NO][O]](/images/math/2/2/c/22c6c68a7dd5ad6b945b412d1fe801a7.png)
The calculation of the reaction rates of each reaction is done in the function omega of the file $FOAM_SRC/thermophysicalModels/chemistryModel/chemistryModel/StandardChemistryModel/StandardChemistryModel.C:
template<class ReactionThermo, class ThermoType>
Foam::scalar Foam::StandardChemistryModel<ReactionThermo, ThermoType>::omega
(
const Reaction<ThermoType>& R,
const scalarField& c,
const scalar T,
const scalar p,
scalar& pf,
scalar& cf,
label& lRef,
scalar& pr,
scalar& cr,
label& rRef
) const
{
const scalar kf = R.kf(p, T, c);
const scalar kr = R.kr(kf, p, T, c);
pf = 1.0;
pr = 1.0;
const label Nl = R.lhs().size();
const label Nr = R.rhs().size();
label slRef = 0;
lRef = R.lhs()[slRef].index;
pf = kf;
for (label s = 1; s < Nl; s++)
{
const label si = R.lhs()[s].index;
if (c[si] < c[lRef])
{
const scalar exp = R.lhs()[slRef].exponent;
pf *= pow(max(c[lRef], 0.0), exp);
lRef = si;
slRef = s;
}
else
{
const scalar exp = R.lhs()[s].exponent;
pf *= pow(max(c[si], 0.0), exp);
}
}
cf = max(c[lRef], 0.0);
{
const scalar exp = R.lhs()[slRef].exponent;
if (exp < 1.0)
{
if (cf > SMALL)
{
pf *= pow(cf, exp - 1.0);
}
else
{
pf = 0.0;
}
}
else
{
pf *= pow(cf, exp - 1.0);
}
}
label srRef = 0;
rRef = R.rhs()[srRef].index;
// Find the matrix element and element position for the rhs
pr = kr;
for (label s = 1; s < Nr; s++)
{
const label si = R.rhs()[s].index;
if (c[si] < c[rRef])
{
const scalar exp = R.rhs()[srRef].exponent;
pr *= pow(max(c[rRef], 0.0), exp);
rRef = si;
srRef = s;
}
else
{
const scalar exp = R.rhs()[s].exponent;
pr *= pow(max(c[si], 0.0), exp);
}
}
cr = max(c[rRef], 0.0);
{
const scalar exp = R.rhs()[srRef].exponent;
if (exp < 1.0)
{
if (cr>SMALL)
{
pr *= pow(cr, exp - 1.0);
}
else
{
pr = 0.0;
}
}
else
{
pr *= pow(cr, exp - 1.0);
}
}
return pf*cf - pr*cr;
}
In order to get the reaction rate of the spices k, the reaction rates of each reaction containing the species k has to be multiplied with the stoichiometric coefficient and summed with a positive sign if the species is a product in with a negative sign if the species is a reactant (see also e.g. https://en.wikipedia.org/wiki/Reaction_rate).
It can be written as (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf and the books cited here):
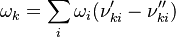
For our example reaction we get:
![\omega_k = \frac{d [X_k]}{dt} = \begin{pmatrix}\frac{d[N_2]}{dt} \\ \frac{d[O]}{dt} \\ \frac{d[NO]}{dt} \\ \frac{d[N]}{dt} \\ \frac{d[O_2]}{dt} \\\end{pmatrix} = \begin{pmatrix} -\omega_1 \\ -\omega_1 + \omega_2 \\ \omega_1 + \omega_2 \\ \omega_1 - \omega_2 \\ \omega_2 \\\end{pmatrix} = \begin{pmatrix} -(k_{f1}[NO][N] - k_{r1}[N2][O]) \\ -(k_{f1}[NO][N] - k_{r1}[N2][O]) + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] - (k_{f2}[N][O2] - k_{r2}[NO][O]) \\ k_{f2}[N][O2] - k_{r2}[NO][O] \\\end{pmatrix}](/images/math/5/4/0/540092492d5d478241d0558e87b6766c.png)
Looking at the above equation we see that the equation describing the evolution of the species concentration is a coupled non--linear differential equation. The calculation of the reaction rates of each species is done in the function of the file $FOAM_SRC/thermophysicalModels/chemistryModel/chemistryModel/StandardChemistryModel/StandardChemistryModel.C:
template<class ReactionThermo, class ThermoType>
void Foam::StandardChemistryModel<ReactionThermo, ThermoType>::omega
(
const scalarField& c,
const scalar T,
const scalar p,
scalarField& dcdt
) const
{
scalar pf, cf, pr, cr;
label lRef, rRef;
dcdt = Zero;
forAll(reactions_, i)
{
const Reaction<ThermoType>& R = reactions_[i];
scalar omegai = omega
(
R, c, T, p, pf, cf, lRef, pr, cr, rRef
);
forAll(R.lhs(), s)
{
const label si = R.lhs()[s].index;
const scalar sl = R.lhs()[s].stoichCoeff;
dcdt[si] -= sl*omegai;
}
forAll(R.rhs(), s)
{
const label si = R.rhs()[s].index;
const scalar sr = R.rhs()[s].stoichCoeff;
dcdt[si] += sr*omegai;
}
}
}
The remaining two quantities to define are the forward and backward reaction rate constants 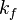 and and 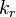 . The forward rate constant is calculated for Arrhenius type reactions as follows (see also [5]): . The forward rate constant is calculated for Arrhenius type reactions as follows (see also [5]):
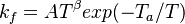
A is the per-exponent factor, Ta the activation temperature and beta is the exponent of the temperature in the calculation of the reaction rate. The soure code can be find in $FOAM_SRC/thermophysicalModels/specie/reaction/reactionRate/ArrheniusReactionRate/ArrheniusReactionRateI.H:
inline Foam::scalar Foam::ArrheniusReactionRate::operator()
(
const scalar p,
const scalar T,
const scalarField&
) const
{
scalar ak = A_;
if (mag(beta_) > VSMALL)
{
ak *= pow(T, beta_);
}
if (mag(Ta_) > VSMALL)
{
ak *= exp(-Ta_/T);
}
return ak;
}
The reverse rate of the ith reaction is calculated as follows (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf) :
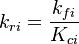
The equilibrium constant is calculated as follows:
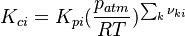
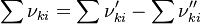 is the sum of the stoichiometric coefficient of the ith reaction. Furthermore is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
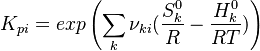
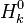 and and 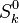 are the molar enthalpy and entropy of the species k . are the molar enthalpy and entropy of the species k .
The reverse rate constant is calculated in the file $FOAM_SRC/thermophysicalModels/specie/reaction/Reactions/ReversibleReaction/ReversibleReaction.C:
template
<
template<class> class ReactionType,
class ReactionThermo,
class ReactionRate
>
Foam::scalar Foam::ReversibleReaction
<
ReactionType,
ReactionThermo,
ReactionRate
>::kr
(
const scalar kfwd,
const scalar p,
const scalar T,
const scalarField& c
) const
{
return kfwd/max(this->Kc(p, T), 1e-6);
}
The calculation of Kc can be found in the file $FOAM_SRC/thermophysicalModels/specie/thermo/thermo/thermoI.H.
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::K(const scalar p, const scalar T) const
{
scalar arg = -this->Y()*this->G(Pstd, T)/(RR*T);
if (arg < 600)
{
return exp(arg);
}
else
{
return VGREAT;
}
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Kp(const scalar p, const scalar T) const
{
return K(p, T);
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Kc(const scalar p, const scalar T) const
{
const scalar nm = this->Y()/this->W();
if (equal(nm, SMALL))
{
return Kp(p, T);
}
else
{
return Kp(p, T)*pow(Pstd/(RR*T), nm);
}
}
3 Evolution of species
{
forAll(Y, specieI)
{
volScalarField& Yi = Y[specieI];
solve
(
fvm::ddt(rho, Yi) - chemistry.RR(specieI),
mesh.solver("Yi")
);
}
}
4 Evolution of energy
The energy equation is derived from the first law of thermodynamics (see also https://en.wikipedia.org/wiki/Enthalpy): For closed systems the change of internal energy is equal to the heat supplied to the system. For open systems the change of enthalpy is equal to the heat supplied to the system. For the first case we get:
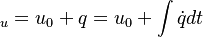
| (x) |
If we add on both sides the pressure divided by the density we get:
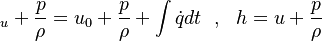
| (x) |
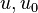 are the internal energy and the internal energy at the time 0. are the internal energy and the internal energy at the time 0.
{
volScalarField& h = thermo.he();
if (constProp == "volume")
{
h[0] = u0 + p[0]/rho[0] + integratedHeat;
}
else
{
h[0] = h0 + integratedHeat;
}
thermo.correct();
}
With the above equation the evolution of the enthalpy with time can be calculated. Knowing the functional dependency of the heat capacity at constant pressure 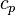 a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here https://caefn.com/openfoam/temperature-calculation. a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here https://caefn.com/openfoam/temperature-calculation.
5 Evolution of the pressure
In order to calculate the pressure Daltons model is used: It says that the thermodynamic pressure can be calculated as the sum of the partial pressures of the individual species (see e.g. https://en.wikipedia.org/wiki/Dalton%27s_law):
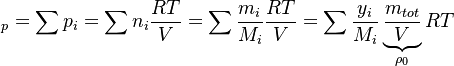
| (x) |
 are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively. are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.
{
rho = thermo.rho();
if (constProp == "volume")
{
scalar invW = 0.0;
forAll(Y, i)
{
invW += Y[i][0]/specieData[i].W();
}
Rspecific[0] = 1000.0*constant::physicoChemical::R.value()*invW;
p[0] = rho0*Rspecific[0]*thermo.T()[0];
rho[0] = rho0;
}
}
Note that the constant 1000 in the above code comes from the fact that in OpenFOAM the molar weight is specified in [kg/kmol]. See the file $FOAM_SRC/thermophysicalModels/specie/specie/specie.H.
6 References
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Powers, Joseph. Combustion thermodynamics and dynamics. Cambridge University Press, 2016.
- ↑ Poinsot, Thierry, and Denis Veynante. Theoretical and numerical combustion. RT Edwards, Inc., 2005.
- ↑ Poinsot, Thierry, and Denis Veynante. Theoretical and numerical combustion. RT Edwards, Inc., 2005.
|
|
|
|
|
|
|
|
|
|
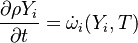
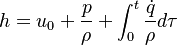
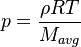
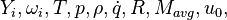 are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
are the species mass mass fraction, the reaction rate, the temperature, the pressure, the density, the heat generated by the combustion, the gas constant, the average molar weight and the initial internal energy, respectively. Note that for a given enthalpy, pressure and density the temperature can be calculated.
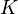 species in
species in  reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
reactions can be expressed in the following form (see also https://www3.nd.edu/~powers/ame.60636/chemkin2000.pdf or the book of [1]):
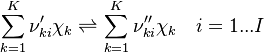
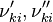 and
and 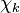 are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie
are the forward, the backward stoichiometric coefficient and the chemical symbol of the specie 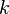 , respectively.
, respectively.
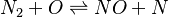
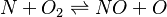
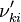 , the backward stoichiometric coefficient
, the backward stoichiometric coefficient 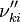 and the chemical symbol of the specie k
and the chemical symbol of the specie k 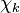 can be written as follows:
can be written as follows:
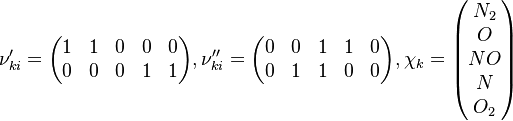
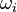 of the reaction i can be written as (see also the book
of the reaction i can be written as (see also the book ![\omega_i = k_{fi} \prod_k [X]_k^{\nu_{ki}'} - k_{ri} \prod_k [X]_k^{\nu_{ki}''}](/images/math/0/8/b/08b53dce9957da556577c563ae8cc9d4.png)
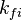 and
and 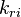 are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients
are the forward and reverse rate constant reaction i. Note that in OpenFoam the default value of the exponents in the above expression are the stoichiometric coefficients ![[X]_k](/images/math/c/b/c/cbc7d65a80a572c296064e8d44295626.png) is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
is the molar concentration of the species k. To continue with our example the reaction rates of the Zeldovich mechanism can be written:
![\omega_1 = k_{f1}[NO][N] - k_{r1}[N2][O]](/images/math/a/7/0/a70bab94d73fb8ba6a8d65ebeb62aa68.png)
![\omega_2 = k_{f2}[N][O2] - k_{r2}[NO][O]](/images/math/2/2/c/22c6c68a7dd5ad6b945b412d1fe801a7.png)
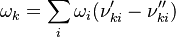
![\omega_k = \frac{d [X_k]}{dt} = \begin{pmatrix}\frac{d[N_2]}{dt} \\ \frac{d[O]}{dt} \\ \frac{d[NO]}{dt} \\ \frac{d[N]}{dt} \\ \frac{d[O_2]}{dt} \\\end{pmatrix} = \begin{pmatrix} -\omega_1 \\ -\omega_1 + \omega_2 \\ \omega_1 + \omega_2 \\ \omega_1 - \omega_2 \\ \omega_2 \\\end{pmatrix} = \begin{pmatrix} -(k_{f1}[NO][N] - k_{r1}[N2][O]) \\ -(k_{f1}[NO][N] - k_{r1}[N2][O]) + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] + k_{f2}[N][O2] - k_{r2}[NO][O] \\ k_{f1}[NO][N] - k_{r1}[N2][O] - (k_{f2}[N][O2] - k_{r2}[NO][O]) \\ k_{f2}[N][O2] - k_{r2}[NO][O] \\\end{pmatrix}](/images/math/5/4/0/540092492d5d478241d0558e87b6766c.png)
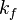 and
and 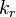 . The forward rate constant is calculated for Arrhenius type reactions as follows (see also
. The forward rate constant is calculated for Arrhenius type reactions as follows (see also 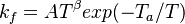
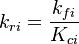
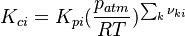
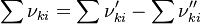 is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
is the sum of the stoichiometric coefficient of the ith reaction. Furthermore
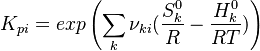
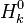 and
and 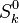 are the molar enthalpy and entropy of the species k .
are the molar enthalpy and entropy of the species k .
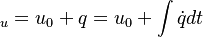
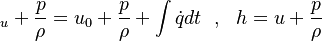
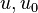 are the internal energy and the internal energy at the time 0.
are the internal energy and the internal energy at the time 0.
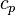 a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here
a relation between the enthalpy and the temperature can be established. For an example of how it is down in OpenFOAM with a polynomial dependency of the heat capacity from the temperature can be found here 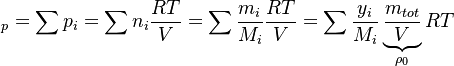
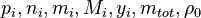 are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.
are the partial pressure, the number of molecules, the mass, the molar mass, the mass faction of the species i, the total mass and the initial density, respectively.