ChtMultiRegionFoam

ChtMultiRegionFoam

   Solver for steady or transient fluid flow and solid heat conduction, with
   conjugate heat transfer between regions, buoyancy effects, turbulence,
   reactions and radiation modelling.

1 Equations

For each region defined as fluid, the according equation for the fluid is solved and the same is done for each solid region. The regions are coupled by a thermal boundary condition.

1.1 Equations Fluid

For each fluid region the compressible Navier Stokes equation are solved.

1.1.1 Mass conservation

The variable-density continuity equation is

$\frac{\partial \rho}{\partial t} + \frac{\partial {\rho u}_j}{\partial x_j} = 0$

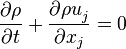(1)

The source code can be found in src/finiteVolume/cfdTools/compressible/rhoEqn.H:

 
 
{
    fvScalarMatrix rhoEqn
    (
        fvm::ddt(rho)
      + fvc::div(phi)
      ==
        fvOptions(rho)
    );
 
    fvOptions.constrain(rhoEqn);
 
    rhoEqn.solve();
 
    fvOptions.correct(rho);
}
 

1.1.2 Momentum conservation

$\frac{ \partial (\rho {u}_i)}{\partial t} + \frac{\partial}{\partial x_j} \left( \rho {u}_j u_i \right) = - \frac{\partial p_{rgh}} {\partial{x_i}} + \frac{\partial \rho g_j x_j}{\partial x_i} + \frac{\partial}{\partial x_j} \left( \tau_{ij} + \tau_{t_{ij}} \right)$

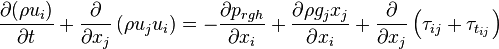(2)

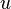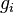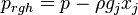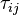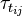$u$ represent the velocity, $g_i$ the gravitational acceleration, $p_{rgh} = p - \rho g_j x_j$ the pressure minus the hydrostatic pressure and $\tau_{ij}$ and $\tau_{t_{ij}}$ are the viscose and turbulent stresses.