ChtMultiRegionFoam
ChtMultiRegionFoam
Solver for steady or transient fluid flow and solid heat conduction, with conjugate heat transfer between regions, buoyancy effects, turbulence, reactions and radiation modelling.
Contents
1 Equations
For each region defined as fluid, the according equation for the fluid is solved and the same is done for each solid region. The regions are coupled by a thermal boundary condition. A short description of the solver can be found also in [1]
1.1 Equations Fluid
For each fluid region the compressible Navier Stokes equation are solved.
1.1.1 Mass conservation
The variable-density continuity equation is
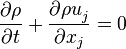 | (1) |
The source code can be found in src/finiteVolume/cfdTools/compressible/rhoEqn.H:
{ fvScalarMatrix rhoEqn ( fvm::ddt(rho) + fvc::div(phi) == fvOptions(rho) ); fvOptions.constrain(rhoEqn); rhoEqn.solve(); fvOptions.correct(rho); }
1.1.2 Momentum conservation
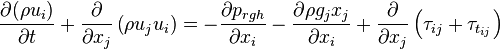 | (2) |
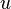 represent the velocity,
represent the velocity, 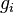 the gravitational acceleration,
the gravitational acceleration, 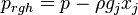 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
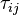 and
and 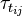 are the viscose and turbulent stresses.
are the viscose and turbulent stresses.
The source code can be found in Ueqn.H:
// Solve the Momentum equation
MRF.correctBoundaryVelocity(U);
tmp<fvVectorMatrix> tUEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence.divDevRhoReff(U)
==
fvOptions(rho, U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}
fvOptions.correct(U);
1.1.3 Energy conservation
The energy equation can be found in: https://cfd.direct/openfoam/energy-equation/
The total energy of a fluid element can be seen as the sum of kinetic energy 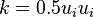 and internal energy
and internal energy  .
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
.
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
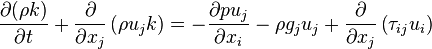 | (3) |
The rate of change of the internal energy  of a fluid element is the heat transferred to this fluid element by diffusion and turbulence
of a fluid element is the heat transferred to this fluid element by diffusion and turbulence 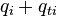 plus the
heat source term
plus the
heat source term  plus the heat source by radiation
plus the heat source by radiation 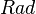 :
:
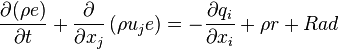 | (4) |
The change rate of the total energy is the sum of the above two equations:
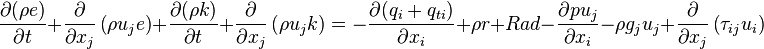 | (5) |
Instead of the internal energy  there is also the option to solve the equation for the enthalpy
there is also the option to solve the equation for the enthalpy 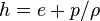 :
:
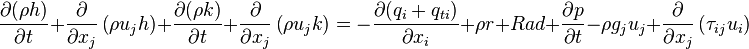 | (5) |
The source code can be found in EEqn.H:
{ volScalarField& he = thermo.he(); fvScalarMatrix EEqn ( fvm::ddt(rho, he) + fvm::div(phi, he) + fvc::ddt(rho, K) + fvc::div(phi, K) + ( he.name() == "e" ? fvc::div ( fvc::absolute(phi/fvc::interpolate(rho), U), p, "div(phiv,p)" ) : -dpdt ) - fvm::laplacian(turbulence.alphaEff(), he) == rho*(U&g) + rad.Sh(thermo, he) + Qdot + fvOptions(rho, he) ); EEqn.relax(); fvOptions.constrain(EEqn); EEqn.solve(); fvOptions.correct(he); thermo.correct(); rad.correct(); Info<< "Min/max T:" << min(thermo.T()).value() << ' ' << max(thermo.T()).value() << endl; }
1.1.4 Species conservation
In order to account for the chemical reactions occurring between different chemical species a conservation equation for each species k has to be solved:
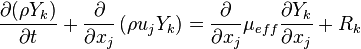 | (6) |
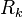 is the reaction rate of the species k.
is the reaction rate of the species k.
The source code can be found in YEqn.H:
tmp<fv::convectionScheme<scalar>> mvConvection(nullptr); if (Y.size()) { mvConvection = tmp<fv::convectionScheme<scalar>> ( fv::convectionScheme<scalar>::New ( mesh, fields, phi, mesh.divScheme("div(phi,Yi_h)") ) ); } { reaction.correct(); Qdot = reaction.Qdot(); volScalarField Yt ( IOobject("Yt", runTime.timeName(), mesh), mesh, dimensionedScalar("Yt", dimless, 0) ); forAll(Y, i) { if (i != inertIndex && composition.active(i)) { volScalarField& Yi = Y[i]; fvScalarMatrix YiEqn ( fvm::ddt(rho, Yi) + mvConvection->fvmDiv(phi, Yi) - fvm::laplacian(turbulence.muEff(), Yi) == reaction.R(Yi) + fvOptions(rho, Yi) ); YiEqn.relax(); fvOptions.constrain(YiEqn); YiEqn.solve(mesh.solver("Yi")); fvOptions.correct(Yi); Yi.max(0.0); Yt += Yi; } } if (Y.size()) { Y[inertIndex] = scalar(1) - Yt; Y[inertIndex].max(0.0); } }
1.2 Equations Solid
For the solid regions only the energy equation has to be solved. The energy equation states that the temporal change of enthalpy of the solid is equal to the divergence of the heat conducted through the solid:
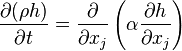 | (7) |
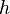 is the specific enthalpy,
is the specific enthalpy, 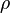 the density and
the density and 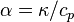 is the thermal
diffusivity which is defined as the ratio between the thermal conductivity
is the thermal
diffusivity which is defined as the ratio between the thermal conductivity 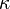 and the specific heat capacity
and the specific heat capacity
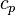 . Note that
. Note that 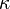 can be also anisotropic.
can be also anisotropic.
2 Source Code
3 References
- ↑ EL ABBASSIA, M.; LAHAYE, D. J. P.; VUIK, C. MODELLING TURBULENT COMBUSTION COUPLED WITH CONJUGATE HEAT TRANSFER IN OPENFOAM.