fireFoam
Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling.
Contents
1 Solution Strategy
The source code can be found in fireFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | Copyright (C) 2011-2017 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application fireFoam Group grpCombustionSolvers Description Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "turbulentFluidThermoModel.H" #include "basicReactingCloud.H" #include "surfaceFilmModel.H" #include "pyrolysisModelCollection.H" #include "radiationModel.H" #include "SLGThermo.H" #include "solidChemistryModel.H" #include "psiReactionThermo.H" #include "CombustionModel.H" #include "pimpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Transient solver for fires and turbulent diffusion flames" " with reacting particle clouds, surface film and pyrolysis modelling." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" #include "createTimeControls.H" #include "compressibleCourantNo.H" #include "setInitialDeltaT.H" #include "createRegionControls.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (runTime.run()) { #include "readTimeControls.H" #include "compressibleCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setMultiRegionDeltaT.H" #include "setDeltaT.H" ++runTime; Info<< "Time = " << runTime.timeName() << nl << endl; parcels.evolve(); surfaceFilm.evolve(); if(solvePyrolysisRegion) { pyrolysis.evolve(); } if (solvePrimaryRegion) { #include "rhoEqn.H" // --- PIMPLE loop while (pimple.loop()) { #include "UEqn.H" #include "YEEqn.H" // --- Pressure corrector loop while (pimple.correct()) { #include "pEqn.H" } if (pimple.turbCorr()) { turbulence->correct(); } } rho = thermo.rho(); } runTime.write(); runTime.printExecutionTime(Info); } Info<< "End" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Equations Liquid Film
The equation describing the evolution of the liquid film can be found in http://www.ilasseurope.org/ICLASS/iclass2012_Heidelberg/Contributions/Paper-pdfs/Contribution1294_b.pdf and https://www.witpress.com/Secure/elibrary/papers/MPF11/MPF11020FU1.pdf. A description of the method used to derive the equation can be found in https://www.researchgate.net/profile/Petr_Vita/publication/313655371_Thin_Film_Fluid_Flow_Simulation_on_Rotating_Discs/links/58a1a592a6fdccf5e9707665/Thin-Film-Fluid-Flow-Simulation-on-Rotating-Discs.pdf.
The conservation of mass reads:
 | (1) |
 represents the mean film velocity,
represents the mean film velocity, 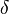 the film height and
the film height and 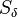 mass source term resulting
from the impingement of the liquid droplets on the film surface.
The momentum conservation reads:
mass source term resulting
from the impingement of the liquid droplets on the film surface.
The momentum conservation reads:
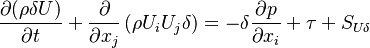 | (2) |
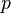 represents the pressure,
represents the pressure, 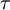 the stress like components of the forces acting on the filme and
the stress like components of the forces acting on the filme and 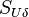 represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects
represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects 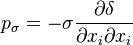 , the hydrostatic contribution
, the hydrostatic contribution 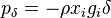 and the contribution of the pressure originated by the surrounding gas
and the contribution of the pressure originated by the surrounding gas 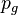 .
. 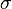 represents the surface tension. The stress like contribution is divided in the wall shear stress
represents the surface tension. The stress like contribution is divided in the wall shear stress 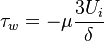 , the gravity force tangential to the wall
, the gravity force tangential to the wall 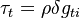 and the contribution of the contact line force
and the contribution of the contact line force 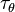 .
. 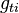 is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
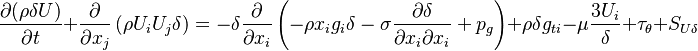 | (3) |
The energy equation reads:
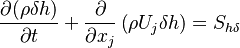 | (4) |
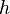 represents the mean film enthalpy and
represents the mean film enthalpy and 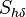 represents the contribution of the impinging droplets to the
energy equation.
represents the contribution of the impinging droplets to the
energy equation.
Equations (1), (3) and (4) represent a system of 3 non-linear partial differential equations with the unknowns 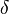 ,
, 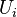 and
and 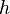 . In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
. In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
1. Solve continuity equation (1). Here has to be mentioned that the quantity solved for is 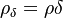 which appears also in the momentum and energy equation.
which appears also in the momentum and energy equation.
2. Solve momentum equation (3)
3. Solve energy equation (4)
4. Solve film thickness equation: The film thickness equation is derived by inserting the discrete momentum equation into the continuity equation.
Steps 2-4 are solved a number of time specified by the user in order to achieve sufficient convergence of the equations.
2.2 Equations Fluid
2.2.1 Momentum conservation
The equation of motion are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
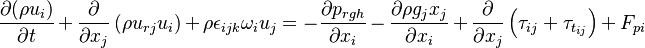 | (2) |
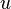 represent the velocity,
represent the velocity, 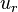 the relative veloicty,
the relative veloicty, 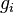 the gravitational acceleration,
the gravitational acceleration, 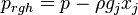 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
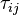 and
and 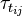 are the viscose and turbulent stresses. Note that since the relative velocity
are the viscose and turbulent stresses. Note that since the relative velocity 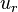 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux  appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
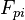 represents the force excreted by the particles on the fluid.
represents the force excreted by the particles on the fluid.
The source code can be found in Ueqn.H:
MRF.correctBoundaryVelocity(U);
fvVectorMatrix UEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence->divDevRhoReff(U)
==
parcels.SU(U)
+ fvOptions(rho, U)
);
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}