fireFoam
Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling.
Contents
1 Solution Strategy
The source code can be found in fireFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | Copyright (C) 2011-2017 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application fireFoam Group grpCombustionSolvers Description Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "turbulentFluidThermoModel.H" #include "basicReactingCloud.H" #include "surfaceFilmModel.H" #include "pyrolysisModelCollection.H" #include "radiationModel.H" #include "SLGThermo.H" #include "solidChemistryModel.H" #include "psiReactionThermo.H" #include "CombustionModel.H" #include "pimpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Transient solver for fires and turbulent diffusion flames" " with reacting particle clouds, surface film and pyrolysis modelling." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" #include "createTimeControls.H" #include "compressibleCourantNo.H" #include "setInitialDeltaT.H" #include "createRegionControls.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (runTime.run()) { #include "readTimeControls.H" #include "compressibleCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setMultiRegionDeltaT.H" #include "setDeltaT.H" ++runTime; Info<< "Time = " << runTime.timeName() << nl << endl; parcels.evolve(); surfaceFilm.evolve(); if(solvePyrolysisRegion) { pyrolysis.evolve(); } if (solvePrimaryRegion) { #include "rhoEqn.H" // --- PIMPLE loop while (pimple.loop()) { #include "UEqn.H" #include "YEEqn.H" // --- Pressure corrector loop while (pimple.correct()) { #include "pEqn.H" } if (pimple.turbCorr()) { turbulence->correct(); } } rho = thermo.rho(); } runTime.write(); runTime.printExecutionTime(Info); } Info<< "End" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Equations Liquid Film
The equation describing the evolution of the liquid film can be found in http://www.ilasseurope.org/ICLASS/iclass2012_Heidelberg/Contributions/Paper-pdfs/Contribution1294_b.pdf and https://www.witpress.com/Secure/elibrary/papers/MPF11/MPF11020FU1.pdf. A description of the method used to derive the equation can be found in https://www.researchgate.net/profile/Petr_Vita/publication/313655371_Thin_Film_Fluid_Flow_Simulation_on_Rotating_Discs/links/58a1a592a6fdccf5e9707665/Thin-Film-Fluid-Flow-Simulation-on-Rotating-Discs.pdf.
The conservation of mass reads:
 | (1) |
 represents the mean film velocity,
represents the mean film velocity, 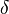 the film height and
the film height and 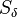 mass source term resulting
from the impingement of the liquid droplets on the film surface. The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
mass source term resulting
from the impingement of the liquid droplets on the film surface. The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveContinuity() { if (debug) { InfoInFunction << endl; } solve ( fvm::ddt(deltaRho_) + fvc::div(phi_) == - rhoSp_ ); }
The momentum conservation reads:
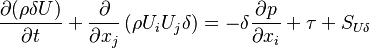 | (2) |
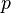 represents the pressure,
represents the pressure, 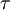 the stress like components of the forces acting on the filme and
the stress like components of the forces acting on the filme and 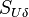 represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects
represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects 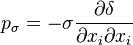 , the hydrostatic contribution
, the hydrostatic contribution 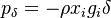 and the contribution of the pressure originated by the surrounding gas
and the contribution of the pressure originated by the surrounding gas 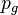 .
. 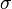 represents the surface tension. The stress like contribution is divided in the wall shear stress
represents the surface tension. The stress like contribution is divided in the wall shear stress 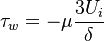 , the gravity force tangential to the wall
, the gravity force tangential to the wall 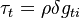 and the contribution of the contact line force
and the contribution of the contact line force 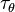 .
. 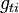 is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
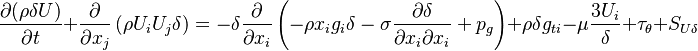 | (3) |
The source code of the momentum equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
tmp<Foam::fvVectorMatrix> kinematicSingleLayer::solveMomentum ( const volScalarField& pu, const volScalarField& pp ) { if (debug) { InfoInFunction << endl; } // Momentum tmp<fvVectorMatrix> tUEqn ( fvm::ddt(deltaRho_, U_) + fvm::div(phi_, U_) == - USp_ // - fvm::SuSp(rhoSp_, U_) - rhoSp_*U_ + forces_.correct(U_) + turbulence_->Su(U_) ); fvVectorMatrix& UEqn = tUEqn.ref(); UEqn.relax(); if (momentumPredictor_) { solve ( UEqn == fvc::reconstruct ( - fvc::interpolate(delta_) * ( regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) + fvc::snGrad(delta_)*fvc::interpolate(pp) ) - fvc::flux(rho_*gTan()) ) ) ); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); } return tUEqn; }
The energy equation reads:
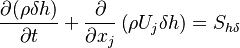 | (4) |
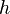 represents the mean film enthalpy and
represents the mean film enthalpy and 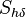 represents the contribution of the impinging droplets to the
energy equation. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
represents the contribution of the impinging droplets to the
energy equation. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
void thermoSingleLayer::solveEnergy() { if (debug) { InfoInFunction << endl; } dimensionedScalar residualDeltaRho ( "residualDeltaRho", deltaRho_.dimensions(), 1e-10 ); solve ( fvm::ddt(deltaRho_, hs_) + fvm::div(phi_, hs_) == - hsSp_ + q(hs_) + radiation_->Shs() ); correctThermoFields(); // Evaluate viscosity from user-model viscosity_->correct(pPrimary_, T_); // Update film wall and surface temperatures updateSurfaceTemperatures(); }
The last equation missing is the linear equation used to get the film thickness 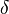 . In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P
. In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P 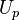 which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
![\rho \bold {U_p} \delta = \rho \left [ \bold { H[U] } \bold {\frac {1}{A_P}} - \bold {\frac {1}{A_P}}\delta \nabla \left ( \underbrace{-\rho g_i x_i}_{P_p} \delta - \underbrace{\sigma \nabla \nabla \delta + p_g}_{P_u} \right ) + \bold {\frac {1}{A_P}}\rho \delta g_t \right ] \delta](/images/math/1/4/4/1449081c4710027a4a917a67b76e63d8.png) | (5) |
The operator ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the
contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
![\rho \nabla \cdot \left ( \bold {U_p} \delta \right ) =
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \bold {\frac {\delta}{A_P}} \nabla \left ( {P_p} \delta - {P_u} \right ) + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right )](/images/math/3/4/8/3487ae3676dcee945a6407c1b602abe7.png) | (6) |
The above equation can be inserted into the continuity equation to obtain:
![\frac{ \partial (\rho \delta )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {\delta^2}{A_P} \nabla {P_p} - \frac {\delta P_p}{A_P} \nabla {\delta} + \bold {\frac {\delta}{A_P}} \nabla {P_u} + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right ) = S_{\delta}](/images/math/f/9/9/f99b3666e1dcc41ab13ea6a5b628d7d8.png) | (7) |
It is obvious that the above equation is non linear in 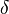 . In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
. In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k P_p}{A_P} \nabla {\delta^{k+1}} + \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) = S_{\delta}](/images/math/5/4/0/540d1216fcbedc792a23c33ea0a06a6e.png) | (8) |
The superscript k denote the solution computed at the last iteration an the superscript k+1 denotes the solution of the current iteration which has to be computed by solving the linear system resulting from the discretization. After separating the linear and the still non linear terms of the above equation we obtain:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} + \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k+1} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/1/4/1/14184b7a1a7ddd34ddd53e7753d3b1c5.png) | (9) |
Since the above equation still contains a non linear contribution it has remaining 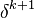 has to be approximated by the value at the previous iteration step
has to be approximated by the value at the previous iteration step
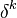 :
:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} + \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/7/6/5/7651e0e119760466c356531a7a3d3fc7.png) | (10) |
which is the final form solved in the present solver. The source code can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveThickness ( const volScalarField& pu, const volScalarField& pp, const fvVectorMatrix& UEqn ) { if (debug) { InfoInFunction << endl; } volScalarField rUA(1.0/UEqn.A()); U_ = rUA*UEqn.H(); surfaceScalarField deltarUAf(fvc::interpolate(delta_*rUA)); surfaceScalarField rhof(fvc::interpolate(rho_)); surfaceScalarField phiAdd ( "phiAdd", regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) ) - fvc::flux(rho_*gTan()) ); constrainFilmField(phiAdd, 0.0); surfaceScalarField phid ( "phid", fvc::flux(U_*rho_) - deltarUAf*phiAdd*rhof ); constrainFilmField(phid, 0.0); surfaceScalarField ddrhorUAppf ( "deltaCoeff", fvc::interpolate(delta_)*deltarUAf*rhof*fvc::interpolate(pp) ); regionMesh().setFluxRequired(delta_.name()); for (int nonOrth=0; nonOrth<=nNonOrthCorr_; nonOrth++) { // Film thickness equation fvScalarMatrix deltaEqn ( fvm::ddt(rho_, delta_) + fvm::div(phid, delta_) - fvm::laplacian(ddrhorUAppf, delta_) == - rhoSp_ ); deltaEqn.solve(); if (nonOrth == nNonOrthCorr_) { phiAdd += fvc::interpolate(pp) * fvc::snGrad(delta_) * regionMesh().magSf(); phi_ == deltaEqn.flux(); } } // Bound film thickness by a minimum of zero delta_.max(0.0); // Update U field U_ -= fvc::reconstruct(deltarUAf*phiAdd); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); // Update film wall and surface velocities updateSurfaceVelocities(); // Continuity check continuityCheck(); }
Equations (1), (3) and (4) represent a system of 3 non-linear partial differential equations with the unknowns 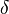 ,
, 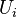 and
and 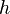 . In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
. In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
1. Solve continuity equation (1). Here has to be mentioned that the quantity solved for is 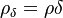 which appears also in the momentum and energy equation.
which appears also in the momentum and energy equation.
2. Solve momentum equation (3)
3. Solve energy equation (4)
4. Solve film thickness equation: The film thickness equation is derived by inserting the discrete momentum equation into the continuity equation.
Steps 2-4 are solved a number of time specified by the user in order to achieve sufficient convergence of the equations. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer
void thermoSingleLayer::evolveRegion() { if (debug) { InfoInFunction << endl; } // Solve continuity for deltaRho_ solveContinuity(); // Update sub-models to provide updated source contributions updateSubmodels(); // Solve continuity for deltaRho_ solveContinuity(); for (int oCorr=1; oCorr<=nOuterCorr_; oCorr++) { // Explicit pressure source contribution tmp<volScalarField> tpu(this->pu()); // Implicit pressure source coefficient tmp<volScalarField> tpp(this->pp()); // Solve for momentum for U_ tmp<fvVectorMatrix> UEqn = solveMomentum(tpu(), tpp()); // Solve energy for hs_ - also updates thermo solveEnergy(); // Film thickness correction loop for (int corr=1; corr<=nCorr_; corr++) { // Solve thickness for delta_ solveThickness(tpu(), tpp(), UEqn()); } } // Update deltaRho_ with new delta_ deltaRho_ == delta_*rho_; // Update temperature using latest hs_ T_ == T(hs_); }
2.2 Equations Fluid
2.2.1 Momentum conservation
The equation of motion are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
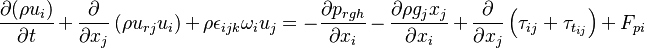 | (2) |
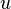 represent the velocity,
represent the velocity, 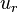 the relative veloicty,
the relative veloicty, 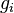 the gravitational acceleration,
the gravitational acceleration, 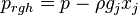 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
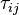 and
and 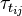 are the viscose and turbulent stresses. Note that since the relative velocity
are the viscose and turbulent stresses. Note that since the relative velocity 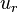 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux  appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
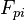 represents the force excreted by the particles on the fluid.
represents the force excreted by the particles on the fluid.
The source code can be found in Ueqn.H:
MRF.correctBoundaryVelocity(U);
fvVectorMatrix UEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence->divDevRhoReff(U)
==
parcels.SU(U)
+ fvOptions(rho, U)
);
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}