Difference between revisions of "RhoSimpleFoam"
(→Solution Strategy) |
|||
| Line 17: | Line 17: | ||
After correcting the velocity field, the equations for turbulence are solved. | After correcting the velocity field, the equations for turbulence are solved. | ||
The above iterative solution procedure is repeated until convergence. | The above iterative solution procedure is repeated until convergence. | ||
| + | |||
| + | A good book which describes the derivation of the pressure equation for compressible cases is the one of <ref> Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016): </ref>. | ||
The source code can be found in rhoSimpleFoam.C | The source code can be found in rhoSimpleFoam.C | ||
| Line 76: | Line 78: | ||
</cpp><br> | </cpp><br> | ||
| + | |||
| + | |||
| + | =References= | ||
| + | <references/> | ||
Revision as of 09:11, 26 November 2020
rhoSimpleFoam
rhoSimpleFoam is a steady-state solver for compressible, turbulent flow, using the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm. In the newer releases it also includes an option to use the SIMPLEC (Semi-Implicit Method for Pressure Linked Equations Consistent) algorithm. It is a pressure based compressible solver. That means that a pressure equation is solved and the density is related to the pressure via an equation of state.
1 Solution Strategy
The solver follows a segregated solution strategy. This means that the equations for each variable characterizing the system (the velocity 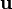 , the pressure
, the pressure 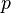 , the energy (either internal energy or enthalpy depending on the choice of the user) and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
, the energy (either internal energy or enthalpy depending on the choice of the user) and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
 which is a function of the velocity and density
which is a function of the velocity and density 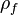 ) is resolved by computing it from the velocity and pressure values of the preceding iteration. Note that the density is related to the pressure via an equation of state which can be selected by the user. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field
) is resolved by computing it from the velocity and pressure values of the preceding iteration. Note that the density is related to the pressure via an equation of state which can be selected by the user. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field  which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the energy equation is solved. Then that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field
which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the energy equation is solved. Then that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field  , which, if inserted in the momentum equation, delivers a divergence free velocity field
, which, if inserted in the momentum equation, delivers a divergence free velocity field 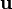 .
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
.
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
A good book which describes the derivation of the pressure equation for compressible cases is the one of [1].
The source code can be found in rhoSimpleFoam.C
int main(int argc, char *argv[]) { argList::addNote ( "Steady-state solver for compressible turbulent flow." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (simple.loop()) { Info<< "Time = " << runTime.timeName() << nl << endl; // Pressure-velocity SIMPLE corrector #include "UEqn.H" #include "EEqn.H" if (simple.consistent()) { #include "pcEqn.H" } else { #include "pEqn.H" } turbulence->correct(); runTime.write(); runTime.printExecutionTime(Info); } Info<< "End\n" << endl; return 0; }
2 References
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):