Difference between revisions of "Sig Turbomachinery MRF Library"
(→Mathematical Relations) |
(→Energy Equation: added derivation for the internal energy) |
||
| Line 188: | Line 188: | ||
== Energy Equation == | == Energy Equation == | ||
| − | |||
| − | |||
<!-- State Equation: http://en.wikipedia.org/wiki/Equation_of_state#Classical_ideal_gas_law --> | <!-- State Equation: http://en.wikipedia.org/wiki/Equation_of_state#Classical_ideal_gas_law --> | ||
| + | |||
| + | The energy equation formulated with the internal energy | ||
| + | |||
| + | <math> e = c_v T \qquad (3.0)</math> | ||
| + | |||
| + | writes as | ||
| + | |||
| + | <math> \varrho \dfrac{d e}{d t} = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{c} \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} \qquad (3.1) </math> | ||
| + | |||
| + | With Eq. 1.4 and Eq. 4, and if one and inserts Eq. 14 into the right hand side, it follows: | ||
| + | |||
| + | <math> \varrho \dfrac{d e}{d t} | ||
| + | = \varrho \dfrac{d^\prime e}{d t} | ||
| + | = \varrho \dfrac{\partial^\prime e}{\partial t} + \varrho \vec{w} \bullet \nabla e | ||
| + | = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \left[ \vec{w} + \vec{u} \right] \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} \qquad (3.2) </math> | ||
| + | |||
| + | <math> \varrho \left( \dfrac{\partial^\prime e}{\partial t} + \vec{w} \bullet \nabla e \right) | ||
| + | = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \underbrace{ \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{u} \right) }_{B1} | ||
| + | + \varrho \dot{q}_s - \nabla \bullet \vec{q} \qquad (3.3) </math> | ||
| + | |||
| + | In cartesian coordinates, the two variables of term B1 are written as: | ||
| + | |||
| + | <math> \sigma = | ||
| + | \left( \begin{array}{ccc} | ||
| + | \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ | ||
| + | \sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\ | ||
| + | \sigma_{xz} & \sigma_{yz} & \sigma_{zz} | ||
| + | \end{array} \right) \qquad (3.4) | ||
| + | </math> | ||
| + | |||
| + | <math> \nabla \vec{u} = | ||
| + | \left( \begin{array}{ccc} | ||
| + | 0 & -\omega_z^\prime & \omega_y^\prime \\ | ||
| + | \omega_z^\prime & 0 & -\omega_x^\prime\\ | ||
| + | -\omega_y^\prime & \omega_x^\prime & 0 | ||
| + | \end{array} \right) \qquad (3.5) | ||
| + | </math> | ||
| + | |||
| + | As the stress tensor is symmetric <math> \sigma = \sigma^T</math>, and thus <math>\sigma_{xy} = \sigma_{yx}</math>; <math>\sigma_{xz} = \sigma_{zx}</math> and <math>\sigma_{zy} = \sigma_{yz}</math>. An the gradient of the rotational speed is skew-symmetric <math> \nabla \vec{u} = - \left( \nabla \vec{u} \right)^T</math> | ||
| + | |||
| + | Thus the double scalar product from term B1 is in cartesian coordinates: | ||
| + | |||
| + | <math> | ||
| + | \begin{alignat}{2} | ||
| + | \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{u} \right) & = | ||
| + | \left( \begin{array}{ccc} | ||
| + | \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ | ||
| + | \sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\ | ||
| + | \sigma_{xz} & \sigma_{yz} & \sigma_{zz} | ||
| + | \end{array} \right) | ||
| + | \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, | ||
| + | \left( \begin{array}{ccc} | ||
| + | 0 & -\omega_z^\prime & \omega_y^\prime \\ | ||
| + | \omega_z^\prime & 0 & -\omega_x^\prime \\ | ||
| + | -\omega_y^\prime & \omega_x^\prime & 0 | ||
| + | \end{array} \right) \\ | ||
| + | & = 0 - \sigma_{xy} \omega_z^\prime + \sigma_{xz} \omega_y^\prime \\ | ||
| + | & + \sigma_{xy} \omega_z^\prime + 0 - \sigma_{yz} \omega_x^\prime \\ | ||
| + | & - \sigma_{xz} \omega_y^\prime + \sigma_{yz} \omega_x^\prime + 0 \\ | ||
| + | & = 0 \qquad \qquad \qquad \qquad \qquad (3.6) | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
| + | Inserting Eq. 3.6 and the continuity equation Eq. 1.18 into to left hand side, results in | ||
| + | |||
| + | <math> | ||
| + | \varrho \left( \dfrac{\partial^\prime e}{\partial t} + \vec{w} \bullet \nabla e \right) | ||
| + | + e \underbrace{ \left( \dfrac{\partial^\prime \varrho}{\partial t} + \nabla \bullet \left( \varrho \vec{w} \right) \right) }_{\text{= 0; s. } Eq. 1.18} | ||
| + | = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} | ||
| + | \qquad (3.7) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \varrho \dfrac{\partial^\prime e}{\partial t} + \left( \varrho\vec{w} \right) \bullet \nabla e | ||
| + | + e \dfrac{\partial^\prime \varrho}{\partial t} + e \left( \nabla \bullet \left( \varrho \vec{w} \right) \right) | ||
| + | = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} | ||
| + | \qquad (3.8) | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \dfrac{\partial^\prime \varrho e}{\partial t} + \nabla \bullet \left( \varrho \vec{w} e \right) | ||
| + | = \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} | ||
| + | \qquad (3.8) | ||
| + | </math> | ||
| + | |||
| + | The stress tensor can be split up into two parts, the thermodynamic pressure and the shear stress tensor | ||
| + | |||
| + | <math> | ||
| + | \sigma = -p \mathbb{G} + \tau \qquad (3.9) | ||
| + | </math> | ||
| + | |||
| + | Inserting Eq. 3.9 into Eq. 3.8 and reducing afterward with Eq. 2.3 yields to | ||
| + | |||
| + | <math> | ||
| + | \begin{alignat}{2} | ||
| + | \dfrac{\partial^\prime \varrho e}{\partial t} | ||
| + | + \nabla \bullet \left( \varrho \vec{w} e \right) | ||
| + | & = \left( -p \mathbb{G} + \tau \right) \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \varrho \dot{q}_s - \nabla \bullet \vec{q} \\ | ||
| + | & = -p \mathbb{G} \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \tau \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \varrho \dot{q}_s - \nabla \bullet \vec{q} \\ | ||
| + | & = -p \left( \nabla \bullet \vec{w} \right) + \tau \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \varrho \dot{q}_s - \nabla \bullet \vec{q} \qquad (3.10) | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
| + | The heat flux can be expressed with the [http://en.wikipedia.org/wiki/Conduction_%28heat%29#Fourier.27s_law Fourier's law], where <math>\lambda</math> is the conductivity. The temperature can be expressed with the internal energy with Eq. 3.0 | ||
| + | |||
| + | <math> | ||
| + | \vec{q} = - \lambda \nabla T = - \lambda \nabla \left( \frac{e}{c_v} \right) \qquad (3.11) | ||
| + | </math> | ||
| + | |||
| + | Inserting Eq. 3.11 into Eq. 3.10, yields to an energy equation for the '''internal energy''' in a relative reference frame, formulated with the relative velocity. | ||
| + | |||
| + | <math> | ||
| + | \dfrac{\partial^\prime \varrho e}{\partial t} | ||
| + | + \nabla \bullet \left( \varrho \vec{w} e \right) | ||
| + | = -p \left( \nabla \bullet \vec{w} \right) + \tau \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \vec{w} \right) | ||
| + | + \varrho \dot{q}_s + \nabla \bullet \left( \lambda \nabla \frac{e}{c_v} \right) \qquad (3.12) | ||
| + | </math> | ||
== Shear Stress Tensor == | == Shear Stress Tensor == | ||
Revision as of 10:28, 18 May 2010
Contents
1 Continuity Equation
1.1 Mathematical Relations
The product rule is also valid with the Nabla-Operator and arbitrary products  and
and  . The arrows above indicates the appliance of the Nabla-Operator.
. The arrows above indicates the appliance of the Nabla-Operator.
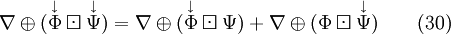
The total time derivation of any variable 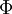 can be split off into a local term and a convective term. In the absolute frame of reference it gives with the absolute velocity
can be split off into a local term and a convective term. In the absolute frame of reference it gives with the absolute velocity 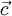
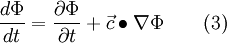
And in the relative frame of reference it gives with the relative velocity 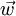
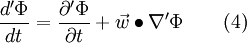
As for a scalar variable it is valid

The first time derivation of any vector 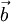 formulated in the absolute and relative frame of reference, according to [1], where
formulated in the absolute and relative frame of reference, according to [1], where 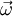 is the angular frequency between these two coordinate systems. Any quantity with an ' is related to the relative frame of reference.
is the angular frequency between these two coordinate systems. Any quantity with an ' is related to the relative frame of reference.

If  is a vector operator, then it is valid
is a vector operator, then it is valid
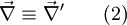
Consider, that the origin of the absolute and relative frame of reference is coincident. Then it is valid to say, that the position vector is equal in both systems 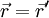 . But, be aware, the components of these vectors are not equal, because they are defined in different base systems. If we now use
. But, be aware, the components of these vectors are not equal, because they are defined in different base systems. If we now use 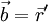 in eq. 1, it gives us the well known relation between the absolute and relative velocity.
in eq. 1, it gives us the well known relation between the absolute and relative velocity.

If one replaces the left and right hand side of eq. 1.4 with the expressions from eq. 3 and eq. 4 one yields for a scalar variable
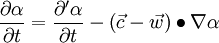
If we insert eq. 2-4 into the 1, one can write for a vector variable
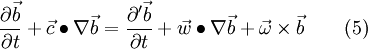
With the relationship of eq. 14 this yields to
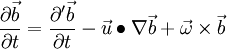
The scalar product of two vectors is commutative [2]:
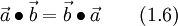
furthermore the following is valid [3]
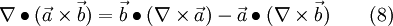
1.2 Transformation in a Relative Frame of Reference
The continuity equation in an inertial frame of reference is written as
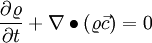
If one now applies Eq. 1.4 and Eq. 14 one gets
![\underbrace{ \frac{\partial^\prime \varrho}{\partial t} - \left( \vec{c} - \vec{w} \right) \bullet \nabla \varrho }_{\frac{\partial \varrho}{\partial t}} + \nabla \bullet [ \varrho \underbrace{ \left( \vec{w} + \vec{\omega} \times \vec{r}^\prime \right) }_\vec{c} ] = 0](/images/math/c/8/d/c8d107c67977d524b24ee413364555f0.png)
If one now uses the general product rule from Eq. 30, one gets
![\frac{\partial^\prime \varrho}{\partial t} - \left( \vec{\omega} \times \vec{r}^\prime \right) \bullet \nabla \varrho
+ \nabla \bullet \left( \varrho \vec{w} \right)
+ \nabla \bullet [ \overset{\downarrow}{ \varrho } ( \vec{\omega} \overset{\downarrow}{ \times } \vec{r}^\prime ) ] = 0 \qquad (1.7)](/images/math/9/3/0/9300bd062fe8b5f8a337fcd3cb01c19d.png)
The last term on the left hand of Eq. 1.7 gets now expanded with Eq. 30, and the second term on the left hand side is changed according to Eq. 1.6
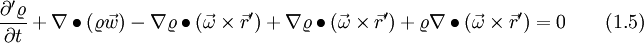
If we now apply eq. 8 to the last term on the left hand side of eq. 1.5, we get
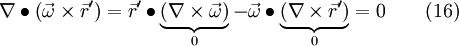
If one consider for example 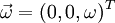 and
and 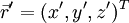 in cartesian coordinates and apply the cross product component-by-component, then the result from eq. 16 maybe become a little bit more clearer.
in cartesian coordinates and apply the cross product component-by-component, then the result from eq. 16 maybe become a little bit more clearer.
The two terms in the mid of the left hand side vanish and according to Eq. 16 the last term on the left hand side is zero. Thus, the continuity equation in the relative frame of reference can be written as
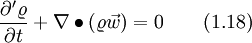
2 Momentum Equation
2.1 Mathematical Relations
The following identities are valid with any vector 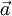 and a scalar
and a scalar 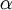 [4]
[4]
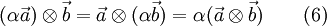
and [5]
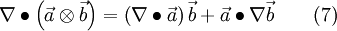
2.2 Transformation in a Relative Frame of Reference
We are now deriving the momentum equation in the relative coordinate system but formulated with the absolute velocity.
If we use eq. 6, then it can be easily shown, that the following statement is valid
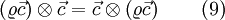
If we use the solution from eq. 9, and apply them to eq. 7, the following can be shown
![\begin{array}{rcl}
\nabla \bullet \left[ \left( \varrho \vec{c} \right) \otimes \vec{c} \right] & = &
\left[\nabla \bullet \left( \varrho \vec{c} \right)\right] \vec{c} + \left( \varrho \vec{c} \right) \bullet \nabla \vec{c} \qquad (10)\\
= \nabla \bullet \left[ \vec{c} \otimes \left( \varrho \vec{c} \right) \right] & = &
\left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right) + \vec{c} \bullet \nabla \left( \varrho \vec{c} \right) \qquad (11)
\end{array}](/images/math/6/d/5/6d558ffa15615010ec9ca0f028765c46.png)
Furthermore, if we apply 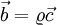 in eq. 5, this gives us
in eq. 5, this gives us
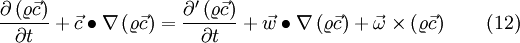
Now we add the first term on the right hand side of eq. 11 ![\left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right)](/images/math/6/4/5/645bc88e0975d376a8c024ab224aa1f2.png) to eq. 12 and apply furthermore eq. 11. Then it follows
to eq. 12 and apply furthermore eq. 11. Then it follows
![\begin{array}{rcl}
\dfrac{\partial \left( \varrho \vec{c} \right)}{\partial t} + \left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right) + \vec{c} \bullet \nabla \left( \varrho \vec{c} \right)
& = & \dfrac{\partial^\prime\left( \varrho \vec{c} \right)}{\partial t} + \vec{w} \bullet \nabla \left( \varrho \vec{c} \right) + \vec{\omega} \times \left( \varrho \vec{c} \right) + \left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right) \\
= \dfrac{\partial \left( \varrho \vec{c} \right)}{\partial t} + \nabla \bullet \left[ \left( \varrho \vec{c} \right) \otimes \vec{c} \right] & = & \dfrac{\partial^\prime\left( \varrho \vec{c} \right)}{\partial t} + \vec{\omega} \times \left( \varrho \vec{c} \right) + \underbrace{\vec{w} \bullet \nabla \left( \varrho \vec{c} \right) + \left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right)}_{A1} \\
\end{array} \qquad (13)](/images/math/7/b/f/7bfaad0cd0468b155ba4ab7f526c2ca4.png)
If we now use the solution from eq. 14 and apply this to the first term on the right hand side of eq. 11, the following is valid
![\begin{array}{rcl}
\left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right)
& = & \left[\nabla \bullet \left( \vec{w}+\vec{u} \right) \right] \left( \varrho \vec{c} \right) \\
& = & \left[\nabla \bullet \vec{w} \right] \left( \varrho \vec{c} \right) + \underbrace{\left[\nabla \bullet \left( \vec{\omega} \times \vec{r}^\prime \right)\right]}_{A2} \left( \varrho \vec{c} \right)
\end{array}\qquad (15)](/images/math/6/8/9/68901056a6d9cef87974929eaf07ccd5.png)
With eq. 16, eq. 15 becomes
![\left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right) = \left[\nabla \bullet \vec{w} \right] \left( \varrho \vec{c} \right) \qquad (17)](/images/math/1/9/5/195ae799f50945f325219041d7048d28.png)
Now with eq. 17 and eq. 7 term A1 from eq. 13 writes to
![\begin{array}{rcl}
\left[\nabla \bullet \vec{c} \right] \left( \varrho \vec{c} \right) + \vec{w} \bullet \nabla \left( \varrho \vec{c} \right) & = & \left[\nabla \bullet \vec{w} \right] \left( \varrho \vec{c} \right) + \vec{w} \bullet \nabla \left( \varrho \vec{c} \right) \\
& = & \nabla \bullet \left[ \vec{w} \otimes \left( \varrho \vec{c} \right) \right]
\end{array}\qquad (18)](/images/math/1/7/0/1708cac6f37df04c88ff377b56a5ba65.png)
If we now insert eq. 18 into eq. 13, we get
![\dfrac{\partial \left( \varrho \vec{c} \right)}{\partial t} + \nabla \bullet \left[ \left( \varrho \vec{c} \right) \otimes \vec{c} \right] = \dfrac{\partial^\prime\left( \varrho \vec{c} \right)}{\partial t} + \nabla \bullet \left[ \vec{w} \otimes \left( \varrho \vec{c} \right) \right] +
\vec{\omega} \times \left( \varrho \vec{c} \right)\qquad (19)](/images/math/6/e/4/6e495172aca9530cb76c8faed6548615.png)
The momentum equation of an inertial coordinate system is equal to
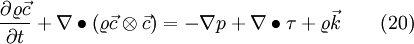
If we now apply eq. 19 to eq. 20 we get the momentum equation in a relative coordinate system, see for example [1]
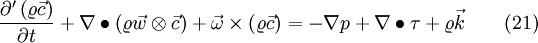
Furthermore it can be shown that the tensor 2. rank from the dyadic product of 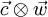 is not symmetric, if you write it down component-by-component in cartesian coordinates. So that it must be valid to write
is not symmetric, if you write it down component-by-component in cartesian coordinates. So that it must be valid to write
3 Energy Equation
The energy equation formulated with the internal energy
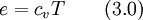
writes as
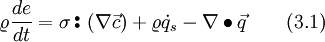
With Eq. 1.4 and Eq. 4, and if one and inserts Eq. 14 into the right hand side, it follows:
![\varrho \dfrac{d e}{d t}
= \varrho \dfrac{d^\prime e}{d t}
= \varrho \dfrac{\partial^\prime e}{\partial t} + \varrho \vec{w} \bullet \nabla e
= \sigma \,{\scriptscriptstyle \stackrel{\bullet}{\bullet}}\, \left( \nabla \left[ \vec{w} + \vec{u} \right] \right) + \varrho \dot{q}_s - \nabla \bullet \vec{q} \qquad (3.2)](/images/math/f/2/c/f2c1df29e4c6931ddcc9b245f1a2d657.png)
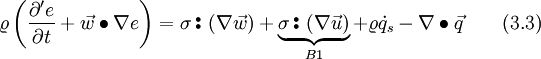
In cartesian coordinates, the two variables of term B1 are written as:
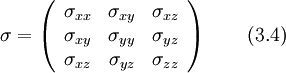
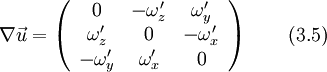
As the stress tensor is symmetric 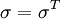 , and thus
, and thus 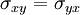 ;
; 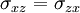 and
and 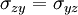 . An the gradient of the rotational speed is skew-symmetric
. An the gradient of the rotational speed is skew-symmetric 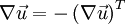
Thus the double scalar product from term B1 is in cartesian coordinates:
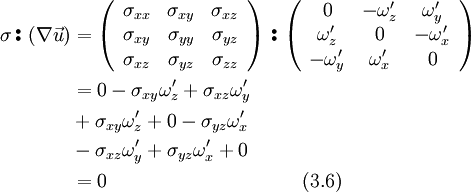
Inserting Eq. 3.6 and the continuity equation Eq. 1.18 into to left hand side, results in
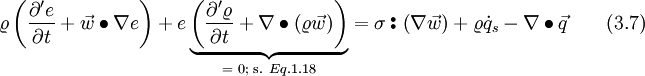
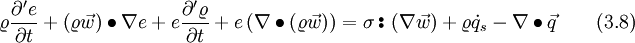
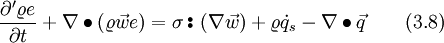
The stress tensor can be split up into two parts, the thermodynamic pressure and the shear stress tensor
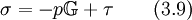
Inserting Eq. 3.9 into Eq. 3.8 and reducing afterward with Eq. 2.3 yields to
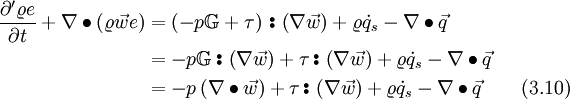
The heat flux can be expressed with the Fourier's law, where 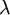 is the conductivity. The temperature can be expressed with the internal energy with Eq. 3.0
is the conductivity. The temperature can be expressed with the internal energy with Eq. 3.0
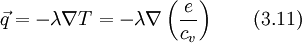
Inserting Eq. 3.11 into Eq. 3.10, yields to an energy equation for the internal energy in a relative reference frame, formulated with the relative velocity.
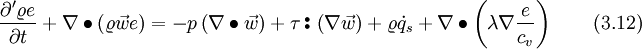
4 Shear Stress Tensor
4.1 Mathematical Relations
For a cross product of two vectors it is valid
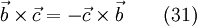
In general one writes for a tensor 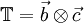 :
:
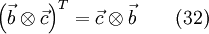
And for a tensor 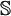 one can also write
one can also write
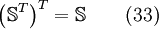
Furthermore for a tensor 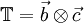 it is valid [2]:
it is valid [2]:
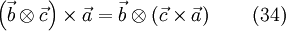
and also
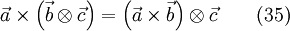
Therefore the following indentities are valid, starting with eq. 34:
![\begin{alignat}{2}
\left( \vec{b} \otimes \vec{c}\right) \times \vec{a} & = & \vec{b} \otimes \left( \vec{c} \times \vec{a}\right) \qquad \qquad \\
\text{with eq. 31 follows: } & = & - \vec{b} \otimes \left( \vec{a} \times \vec{c}\right) \qquad (36) \\
\text{with eq. 32 follows: } & = & - \left[ \left( \vec{a} \times \vec{c}\right) \otimes \vec{b} \right]^T \qquad (37)\\
\text{with eq. 35 follows: } & = & - \left[ \vec{a} \times \left( \vec{c} \otimes \vec{b} \right) \right]^T \qquad (38)\\
\text{with eq. 32 follows: } & = & - \left[ \vec{a} \times \left( \vec{b} \otimes \vec{c} \right)^T \right]^T \qquad (39)
\end{alignat}](/images/math/f/e/e/fee760a2a41a0e1dfe905fb6b6beaec5.png)
With eq. 39 for the tensor 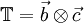 the following is valid:
the following is valid:
![\mathbb{T} \times \vec{a} = - \left[ \vec{a} \times \mathbb{T}^T \right]^T \qquad (40)](/images/math/e/f/2/ef2e70ce29e8f70204d30f5366bfac55.png)
If eq. 40 gets transposed and then eq. 33 is applied to the result, one yields:
![\left( \mathbb{T} \times \vec{a} \right)^T = - \left( \left[ \vec{a} \times \mathbb{T}^T \right]^T \right)^T = - \left( \vec{a} \times \mathbb{T}^T \right) \qquad (41)](/images/math/f/c/0/fc073f1cd7e9819ac72b7b442a0fd011.png)
4.2 Transformation in a Relative Frame of Reference
For a newtonian fluid the shear stress tensor 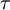 can be expressed in the inertial frame of reference with
can be expressed in the inertial frame of reference with 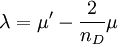 as
as
![\tau = \mu \left[ \nabla \vec{c} + \left( \nabla \vec{c} \right)^T \right] + \lambda \nabla \bullet \vec{c} \qquad (50)](/images/math/2/8/8/28867715c781e11eedc13dd5cf0fc792.png)
Where in three-dimensional the number of dimensions 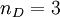 . Furthermore the volume viscosity
. Furthermore the volume viscosity 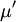 vanishes after Stokes' hypotheses.
vanishes after Stokes' hypotheses.
As already expressed in eq. 16, the last term on the right hand side is equal to
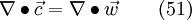
The same procedure is also applied to the following expression
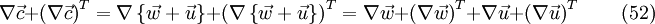
For the last two terms on the right hand side, one can write:
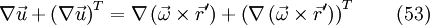
If one now applies the product rule from eq. 30, one yields the following:
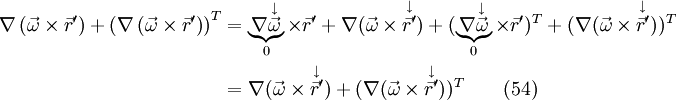
As 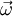 is a single vector and not a vector field, the gradient of a single vector is always zero. If one now apply eq. 36 and eq. 34 at each term of the right hand side of eq. 54, one yields with the metric tensor
is a single vector and not a vector field, the gradient of a single vector is always zero. If one now apply eq. 36 and eq. 34 at each term of the right hand side of eq. 54, one yields with the metric tensor  :
:
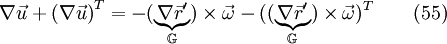
With the help of eq. 41 it follows:
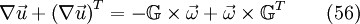
As the metric tensor  is symmetric, one can write
is symmetric, one can write 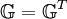 . Thus from eq. 56 it follows
. Thus from eq. 56 it follows
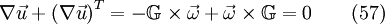
With the help of eq. 57 it follows for eq. 52:
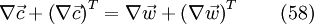
Finally with eq. 51 and eq. 58 the shear stress tensor for a newtonian fluid in the relative frame of reference can be expressed as
![\tau = \mu \left[ \nabla \vec{w} + \left( \nabla \vec{w} \right)^T \right] + \lambda \nabla \bullet \vec{w} \qquad (59)](/images/math/3/3/9/33945873d7472267c79b363bcd3fb2a1.png)
5 References
- ↑ FLUENT 6.3 User's Guide; "Equations for a Rotating Reference Frame"; Chap. 10.2.2
- ↑ Michael H. Vavra, "Aero-thermodynamics and flow in turbomachines", 1960; Appendix B1