Olivier Brugiere, Universite Joseph Fourier, Grenoble, France
Contents
1 Motivation
- Test avaiable subgrid scale (SGS) model
- Test wall model on easy configuration:
- no pressure gradients
- cheap calculation
- easy to mesh
- ...
- Many DNS data base can be found (ex: the Kawmura laboratory [[1]]) to compare mean velocity and rms profiles
2 Testcase description
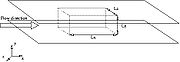
2.1 Flow configuration
2.1.1 Boundary condition
- Streamwise condition : periodicity
- Spanwise condition : periodicity
- Normal to streamwise : two walls
2.1.2 Geometrical Parameters
The Reynodls number of the flow is the same as Abe et al. [3] (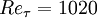 ). Thus the geometry is :
). Thus the geometry is :
- Streamwise distance :
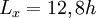
- Normal wall heigh :
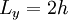
- Spanwise distance :
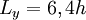
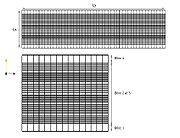
2.2 Mesh generation
We have done the mesh with an automatic tool (*.m4) which is composed by 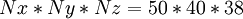 .
The mesh is composed by 4 blocks:
.
The mesh is composed by 4 blocks:
- 2 blocks for the first cell close to the wall. (Hense, y+ can be imposed)
- 2 blocks in the center
2.3 Simulation details
The aim of my study is testing a posteriori near-wall law. We are running three cases :
- Without wall model
- With the Spalding law [1]
- With the Manhart et al. law [2]
3 Numerical results
Results of the simulations are available in the paper written by Duprat et al. [4]
4 References
[1] Spalding, 1961, A single formula for the law of the wall, J. Appl. Mech., vol 28, pp. 455-457
[2] Manhart, Peller, and Brun, 2008, Near-wall scaling for turbulent boundary layers with adverse pressure gradient, Theor. Comput. Fluid Dyn., vol 22 , pp. 243-260.
[3] Abe, Kawamura and Matsuo, Surface heat-flux fluctuations in a turbulent channel flow up to 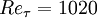 with Pr = 0,025 and 0,71, 2004, Int. J. Heat and Fluid Flow, vol 25, pp. 404-419.
with Pr = 0,025 and 0,71, 2004, Int. J. Heat and Fluid Flow, vol 25, pp. 404-419.
[4] Duprat, Balarac, Métais, Congedo, and Brugière, 2011, A wall-layer model for large-eddy simulations of turbulent flows with/out pressure gradient. Physics of Fluids, 23, 015101.[2]
Back to Validation test cases