Difference between revisions of "SimpleFoam"
(→Momentum Equation) |
m (→Step by step analysis of the pressure equation: Added missing <math>) |
||
| (36 intermediate revisions by one other user not shown) | |||
| Line 162: | Line 162: | ||
} | } | ||
| + | </cpp><br> | ||
| + | |||
| + | The source code of the acceleration resulting from the description in a moving frame of reference can be found in the following src/finiteVolume/cfdTools/general/MRF/MRFZoneList.C | ||
| + | |||
| + | <br><cpp> | ||
| + | |||
| + | Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt | ||
| + | ( | ||
| + | const volVectorField& U | ||
| + | ) const | ||
| + | { | ||
| + | tmp<volVectorField> tacceleration | ||
| + | ( | ||
| + | new volVectorField | ||
| + | ( | ||
| + | IOobject | ||
| + | ( | ||
| + | "MRFZoneList:acceleration", | ||
| + | U.mesh().time().timeName(), | ||
| + | U.mesh() | ||
| + | ), | ||
| + | U.mesh(), | ||
| + | dimensionedVector(U.dimensions()/dimTime, Zero) | ||
| + | ) | ||
| + | ); | ||
| + | volVectorField& acceleration = tacceleration.ref(); | ||
| + | |||
| + | forAll(*this, i) | ||
| + | { | ||
| + | operator[](i).addCoriolis(U, acceleration); | ||
| + | } | ||
| + | |||
| + | return tacceleration; | ||
| + | } | ||
| + | |||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | The calculation of the Coriolis force is done in the file src/finiteVolume/cfdTools/general/MRF/MRFZone.C | ||
| + | |||
| + | <br><cpp> | ||
| + | |||
| + | void Foam::MRFZone::addCoriolis | ||
| + | ( | ||
| + | const volVectorField& U, | ||
| + | volVectorField& ddtU | ||
| + | ) const | ||
| + | { | ||
| + | if (cellZoneID_ == -1) | ||
| + | { | ||
| + | return; | ||
| + | } | ||
| + | |||
| + | const labelList& cells = mesh_.cellZones()[cellZoneID_]; | ||
| + | vectorField& ddtUc = ddtU.primitiveFieldRef(); | ||
| + | const vectorField& Uc = U; | ||
| + | |||
| + | const vector Omega = this->Omega(); | ||
| + | |||
| + | forAll(cells, i) | ||
| + | { | ||
| + | label celli = cells[i]; | ||
| + | ddtUc[celli] += (Omega ^ Uc[celli]); | ||
| + | } | ||
| + | } | ||
</cpp><br> | </cpp><br> | ||
| Line 413: | Line 478: | ||
\bold{a_P^* u_P^*} = - \sum_{N} \bold{a_N u_N^*} + \bold b_P + \frac{1 - \alpha}{\alpha}\bold{a_P u_P}^{n-1} - \nabla p_P^{n-1} = \bold {H[u^*] } - \nabla p_P^{n-1} | \bold{a_P^* u_P^*} = - \sum_{N} \bold{a_N u_N^*} + \bold b_P + \frac{1 - \alpha}{\alpha}\bold{a_P u_P}^{n-1} - \nabla p_P^{n-1} = \bold {H[u^*] } - \nabla p_P^{n-1} | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(5)</td></tr></table> |
After dividing the above equation by <math> a_P^* </math> we obtain: | After dividing the above equation by <math> a_P^* </math> we obtain: | ||
| Line 422: | Line 487: | ||
\bold{u_P^*} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } | \bold{u_P^*} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(6)</td></tr></table> |
| + | Note that according to https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse the continuity equation is the same for the relative velocity described in a reference frame subject to a rigid body motion and the velocity described in an inertial frame of | ||
| + | reference. For that reason the following equation are valid for the relative velocity <math>\bold{u_{Pr}^*} = \bold{u_{P}^*} - \bold{\Omega} \times \bold{r} </math> and also the absolute velocity <math> \bold{u_{P}^*} </math>. <math>\bold{r} </math> is the vector from the center of rotation to the position of interest. For this reason we get the equations solve in the case of a moving reference frame simply by adding the term <math> - \bold{\Omega} \times \bold{r} </math> on both sides of equation (6) and continue with the same procedure as described in the following. | ||
<math> a_P^* = \frac{1}{\alpha}a_P</math> are the modified diagonal coefficients of the matrix after the under relaxation. | <math> a_P^* = \frac{1}{\alpha}a_P</math> are the modified diagonal coefficients of the matrix after the under relaxation. | ||
| Line 434: | Line 501: | ||
<center><math> | <center><math> | ||
| − | \bold{u_P} = \frac{\bold {H[u^*] }}{a_P^* } + \frac{\bold {H[u'] }}{a_P^* } | + | \bold{u_P} = \frac{\bold {H[u^*] }}{a_P^* } + \frac{\bold {H[u'] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{\nabla p_P'}{a_P^* } |
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(7)</td></tr></table> |
The equation for the velocity correction can be written as: | The equation for the velocity correction can be written as: | ||
| Line 445: | Line 512: | ||
\bold{u_P'} = - \frac{\sum_{N} \bold{a_N u_N'}}{a_P^* } - \frac{\nabla p_P'}{a_P^* } = \frac{\bold {H[u'] }}{a_P^* } - \frac{\nabla p_P'}{a_P^* } | \bold{u_P'} = - \frac{\sum_{N} \bold{a_N u_N'}}{a_P^* } - \frac{\nabla p_P'}{a_P^* } = \frac{\bold {H[u'] }}{a_P^* } - \frac{\nabla p_P'}{a_P^* } | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(8)</td></tr></table> |
Note that here it is assumed that the diagonal coefficients of the corrector equation are the same as in the momentum equation previously solved. | Note that here it is assumed that the diagonal coefficients of the corrector equation are the same as in the momentum equation previously solved. | ||
| Line 455: | Line 522: | ||
<center><math> | <center><math> | ||
| − | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f + \sum_f \frac{\bold {H[u'] }}{a_P^* }|_f \cdot S_f | + | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f + \sum_f \frac{\bold {H[u'] }}{a_P^* }|_f \cdot S_f - \sum_f \frac{\nabla p_P}{a_P^* }|_f \cdot S_f = 0 |
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(9)</td></tr></table> |
<math> |_f </math> denotes the values evaluated at the face. | <math> |_f </math> denotes the values evaluated at the face. | ||
| Line 470: | Line 537: | ||
<center><math> | <center><math> | ||
| − | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f | + | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f - \sum_f \frac{\nabla p_P}{a_P^* }|_f \cdot S_f = 0 |
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(10)</td></tr></table> |
| + | |||
| + | |||
| + | The source code can be found in pEqn.H: | ||
| + | |||
| + | <br><cpp> | ||
| + | { | ||
| + | volScalarField rAU(1.0/UEqn.A()); | ||
| + | volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); | ||
| + | surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA)); | ||
| + | MRF.makeRelative(phiHbyA); | ||
| + | adjustPhi(phiHbyA, U, p); | ||
| + | |||
| + | tmp<volScalarField> rAtU(rAU); | ||
| + | |||
| + | if (simple.consistent()) | ||
| + | { | ||
| + | rAtU = 1.0/(1.0/rAU - UEqn.H1()); | ||
| + | phiHbyA += | ||
| + | fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf(); | ||
| + | HbyA -= (rAU - rAtU())*fvc::grad(p); | ||
| + | } | ||
| + | |||
| + | tUEqn.clear(); | ||
| + | |||
| + | // Update the pressure BCs to ensure flux consistency | ||
| + | constrainPressure(p, U, phiHbyA, rAtU(), MRF); | ||
| + | |||
| + | // Non-orthogonal pressure corrector loop | ||
| + | while (simple.correctNonOrthogonal()) | ||
| + | { | ||
| + | fvScalarMatrix pEqn | ||
| + | ( | ||
| + | fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA) | ||
| + | ); | ||
| + | |||
| + | pEqn.setReference(pRefCell, pRefValue); | ||
| + | |||
| + | pEqn.solve(); | ||
| + | |||
| + | if (simple.finalNonOrthogonalIter()) | ||
| + | { | ||
| + | phi = phiHbyA - pEqn.flux(); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | #include "continuityErrs.H" | ||
| + | |||
| + | // Explicitly relax pressure for momentum corrector | ||
| + | p.relax(); | ||
| + | |||
| + | // Momentum corrector | ||
| + | U = HbyA - rAtU()*fvc::grad(p); | ||
| + | U.correctBoundaryConditions(); | ||
| + | fvOptions.correct(U); | ||
| + | } | ||
| + | |||
| + | </cpp><br> | ||
====Simplec==== | ====Simplec==== | ||
| Line 485: | Line 609: | ||
\sum_{N} \bold{a_N u_N'} \approx \sum_{N} \bold{a_N u_P'} = \bold{H_1 u_P'} | \sum_{N} \bold{a_N u_N'} \approx \sum_{N} \bold{a_N u_P'} = \bold{H_1 u_P'} | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(11)</td></tr></table> |
Inserting the above approximation into the equation for the velocity correction we get: | Inserting the above approximation into the equation for the velocity correction we get: | ||
| Line 494: | Line 618: | ||
\bold{(a_P^* - H_1) u_P'} = - \nabla p_P' | \bold{(a_P^* - H_1) u_P'} = - \nabla p_P' | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(12)</td></tr></table> |
Solving for the velocity correction: | Solving for the velocity correction: | ||
| Line 504: | Line 628: | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(13)</td></tr></table> |
| − | The above equation formulates an explicit relation between velocity and pressure | + | The above equation formulates an explicit relation between velocity correction and pressure correction. In the next step we write down: |
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
<center><math> | <center><math> | ||
| − | \bold {u_P^*} + \bold{ u_P'} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{1}{a_P^* - H_1 }\nabla p_P' = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} - \frac{1}{a_P^* }\nabla p_P | + | \bold {u_P^*} + \bold{ u_P'} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{1}{a_P^* - H_1 }\nabla p_P' = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} - \frac{1}{a_P^* - H_1 }\nabla p_P |
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(14)</td></tr></table> |
By taking the divergence of the above equation and setting it to zero we obtain the pressure equation for the simplec algorithm: | By taking the divergence of the above equation and setting it to zero we obtain the pressure equation for the simplec algorithm: | ||
| Line 521: | Line 645: | ||
<center><math> | <center><math> | ||
| − | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f - \sum_f \left ( \frac{1}{a_P^*} |_f - \frac{1}{a_P^* |_f - H_1 |_f } \right )\nabla p_P^{n-1} |_f \cdot S_f - \sum_f \frac{1}{a_P^* }\nabla p_P |_f \cdot S_f = 0 | + | \sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f - \sum_f \left ( \frac{1}{a_P^*} |_f - \frac{1}{a_P^* |_f - H_1 |_f } \right )\nabla p_P^{n-1} |_f \cdot S_f - \sum_f \frac{1}{a_P^* - H_1 }\nabla p_P |_f \cdot S_f = 0 |
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(15)</td></tr></table> |
The difference between the pressure equation in the SIMPLE and SIMPLEC consists only in one term. | The difference between the pressure equation in the SIMPLE and SIMPLEC consists only in one term. | ||
| Line 576: | Line 700: | ||
p.relax(); | p.relax(); | ||
| + | // Momentum corrector | ||
| + | U = HbyA - rAtU()*fvc::grad(p); | ||
| + | U.correctBoundaryConditions(); | ||
| + | fvOptions.correct(U); | ||
| + | } | ||
| + | |||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | ====Step by step analysis of the pressure equation==== | ||
| + | |||
| + | In this section we will analyze step by step the pressure equation since this source code does not solve only the pressure equation but executes also the corrector step for the velocity (which is used as initial guess for the solution of the momentum equation in the next iteration step) and for the face flux <math> \Phi_f </math> which is used to discretize the convective terms in the momentum equation. | ||
| + | |||
| + | <br><cpp> | ||
| + | volScalarField rAU(1.0/UEqn.A()); | ||
| + | </cpp><br> | ||
| + | |||
| + | This line computes the field of diagonal entries of the momentum equation required later on to solve the pressure equation: | ||
| + | |||
| + | <math> \bold{ra_P} = \frac{1}{\bold{a_P}} | ||
| + | </math> | ||
| + | |||
| + | Since the reciprocal of the diagonal is required a few times, the division is done once and then it is multiplied where required. This is done since the multiplication are computationally cheaper than the division. | ||
| + | |||
| + | <br><cpp> | ||
| + | volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); | ||
| + | </cpp><br> | ||
| + | |||
| + | The source code can be found in the file $FOAM_SCR/finiteVolume/cfdTools/general/constrainHbyA/constrainHbyA.C | ||
| + | <br><cpp> | ||
| + | Foam::tmp<Foam::volVectorField> Foam::constrainHbyA | ||
| + | ( | ||
| + | const tmp<volVectorField>& tHbyA, | ||
| + | const volVectorField& U, | ||
| + | const volScalarField& p | ||
| + | ) | ||
| + | { | ||
| + | tmp<volVectorField> tHbyANew; | ||
| + | |||
| + | if (tHbyA.isTmp()) | ||
| + | { | ||
| + | tHbyANew = tHbyA; | ||
| + | tHbyANew.ref().rename("HbyA"); | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | tHbyANew = new volVectorField("HbyA", tHbyA); | ||
| + | } | ||
| + | |||
| + | volVectorField& HbyA = tHbyANew.ref(); | ||
| + | volVectorField::Boundary& HbyAbf = HbyA.boundaryFieldRef(); | ||
| + | |||
| + | forAll(U.boundaryField(), patchi) | ||
| + | { | ||
| + | if | ||
| + | ( | ||
| + | !U.boundaryField()[patchi].assignable() | ||
| + | && !isA<fixedFluxExtrapolatedPressureFvPatchScalarField> | ||
| + | ( | ||
| + | p.boundaryField()[patchi] | ||
| + | ) | ||
| + | ) | ||
| + | { | ||
| + | HbyAbf[patchi] = U.boundaryField()[patchi]; | ||
| + | } | ||
| + | } | ||
| + | |||
| + | return tHbyANew; | ||
| + | } | ||
| + | </cpp><br> | ||
| + | |||
| + | The velocity at the boundary face should satisfy following equation: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \bold{u}|_{bf} = \frac{\bold {H[u] }}{a_P }|_{bf} - \frac{\nabla p{}}{a_P }|_{bf} | ||
| + | </math></center> | ||
| + | </td><td width="5%"></td></tr></table> | ||
| + | |||
| + | The subscript bf denoted that the quantity is evaluated at the boundary face. The function constrainHbyA ensures that the field <math> \frac{\bold {H[u] }}{a_P }|_{bf} </math> | ||
| + | does not violate the above equation. The boundary condition fixedFluxExtrapolatedPressure sets the pressure gradient in order that the above equation is satisfied. If we cannot modify the velocity, the function sets the field <math> \frac{\bold {H[u] }}{a_P }|_{bf} = \bold{u}|_{bf} </math> in order that the field <math> \frac{\bold {H[u] }}{a_P }|_{bf} </math> does not contradict the zero gradient boundary condition which should be applied for the pressure if the velocity is fixed. | ||
| + | |||
| + | |||
| + | <br><cpp> | ||
| + | surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA)); | ||
| + | </cpp><br> | ||
| + | |||
| + | The above function performs the following operation: | ||
| + | |||
| + | <math> | ||
| + | \Phi H = \frac{\bold {H[u] }}{a_P }\cdot S_f|_{f} | ||
| + | </math> | ||
| + | |||
| + | It interpolates the field <math> \frac{\bold {H[u] }}{a_P } </math> at the cell faces and makes than the scalar product of the interpolated field with the surface vector <math> \bold{S}_f </math>. The source can be found in $FOAM_SCR/finiteVolume/finiteVolume/fvc/fvcFlux.C | ||
| + | |||
| + | <br><cpp> | ||
| + | Foam::tmp<Foam::surfaceScalarField> Foam::fvc::flux | ||
| + | ( | ||
| + | const volVectorField& vvf | ||
| + | ) | ||
| + | { | ||
| + | return scheme<vector> | ||
| + | ( | ||
| + | vvf.mesh(), | ||
| + | "flux(" + vvf.name() + ')' | ||
| + | )().dotInterpolate(vvf.mesh().Sf(), vvf); | ||
| + | } | ||
| + | </cpp><br> | ||
| + | |||
| + | In a grid which is not deforming and moves with a moving frame of reference the continuity equation has to be satisfied within this grid. This means that the sum of the relative fluxes over the control volumes have to be zero: | ||
| + | |||
| + | <math> | ||
| + | \sum_f \bold{u_R} |_f\cdot \bold{S}_f = 0 | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | \sum_f (\bold{u_I} - \bold{\Omega} \times \bold{R}) |_f\cdot \bold{S}_f = 0 | ||
| + | </math> | ||
| + | |||
| + | <math> \bold{R} </math> is the vector pointing from the origin of the rotation to the face center. | ||
| + | |||
| + | |||
| + | <br><cpp> | ||
| + | MRF.makeRelative(phiHbyA); | ||
| + | </cpp><br> | ||
| + | |||
| + | |||
| + | The source code can be found in $FOAM_SCR/cfdTools/general/MRF/MRFZoneTemplates.C and $FOAM_SCR/cfdTools/general/MRF/MRFZone.C | ||
| + | |||
| + | <br><cpp> | ||
| + | void Foam::MRFZone::makeRelative(surfaceScalarField& phi) const | ||
| + | { | ||
| + | makeRelativeRhoFlux(geometricOneField(), phi); | ||
| + | } | ||
| + | |||
| + | template<class RhoFieldType> | ||
| + | void Foam::MRFZone::makeRelativeRhoFlux | ||
| + | ( | ||
| + | const RhoFieldType& rho, | ||
| + | surfaceScalarField& phi | ||
| + | ) const | ||
| + | { | ||
| + | if (!active_) | ||
| + | { | ||
| + | return; | ||
| + | } | ||
| + | |||
| + | const surfaceVectorField& Cf = mesh_.Cf(); | ||
| + | const surfaceVectorField& Sf = mesh_.Sf(); | ||
| + | |||
| + | const vector Omega = omega_->value(mesh_.time().timeOutputValue())*axis_; | ||
| + | |||
| + | const vectorField& Cfi = Cf; | ||
| + | const vectorField& Sfi = Sf; | ||
| + | scalarField& phii = phi.primitiveFieldRef(); | ||
| + | |||
| + | // Internal faces | ||
| + | forAll(internalFaces_, i) | ||
| + | { | ||
| + | label facei = internalFaces_[i]; | ||
| + | phii[facei] -= rho[facei]*(Omega ^ (Cfi[facei] - origin_)) & Sfi[facei]; | ||
| + | } | ||
| + | |||
| + | makeRelativeRhoFlux(rho.boundaryField(), phi.boundaryFieldRef()); | ||
| + | } | ||
| + | </cpp><br> | ||
| + | |||
| + | This call ensures that the global mass balance is satisfied if one sets a refence pressure. For more details see the thread https://www.cfd-online.com/Forums/openfoam-programming-development/83876-pref-adjustphi.html. | ||
| + | |||
| + | <br><cpp> | ||
| + | adjustPhi(phiHbyA, U, p); | ||
| + | </cpp><br> | ||
| + | |||
| + | <br><cpp> | ||
| + | tmp<volScalarField> rAtU(rAU); | ||
| + | </cpp><br> | ||
| + | |||
| + | This if condition computes the fields required for the simplec method. | ||
| + | |||
| + | Furthermore it already adds the velocity correction to the field HbyA. | ||
| + | |||
| + | <math> | ||
| + | |||
| + | \bold{HbyA} = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} | ||
| + | |||
| + | </math> | ||
| + | |||
| + | This field is later used to compute the corrected velocity to be used as initial condition for the next iteration of the momentum equation. | ||
| + | |||
| + | <br><cpp> | ||
| + | if (simple.consistent()) | ||
| + | { | ||
| + | rAtU = 1.0/(1.0/rAU - UEqn.H1()); | ||
| + | phiHbyA += | ||
| + | fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf(); | ||
| + | HbyA -= (rAU - rAtU())*fvc::grad(p); | ||
| + | } | ||
| + | |||
| + | tUEqn.clear(); | ||
| + | </cpp><br> | ||
| + | |||
| + | This function updates the pressure gradient for the patches where a fixedFluxPressure boundary condition is chosen | ||
| + | |||
| + | <br><cpp> | ||
| + | // Update the pressure BCs to ensure flux consistency | ||
| + | constrainPressure(p, U, phiHbyA, rAtU(), MRF); | ||
| + | </cpp><br> | ||
| + | |||
| + | For the simple method the velocity at point P con be written: | ||
| + | |||
| + | <math> | ||
| + | \bold {u_P} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{1}{a_P^* }\nabla p_P | ||
| + | </math> | ||
| + | |||
| + | For the simplec method the velocity obtains following expression: | ||
| + | |||
| + | <math> | ||
| + | \bold {u_P} = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} - \frac{1}{a_P^* - H_1 }\nabla p_P | ||
| + | </math> | ||
| + | |||
| + | If we add <math> - \bold{\Omega}\times \bold{R} </math> to the above expression and make the dot product with the surface are vector <math> \bold{S}_f </math> we get for the simple method | ||
| + | |||
| + | <math> | ||
| + | (\bold {u_P} - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f = \underbrace{ (\frac{\bold {H[u^*] }}{a_P^* } - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f}_{\text{phiHbyA}} - \underbrace{\frac{1}{a_P^* }}_{\text{ rAtU}}\nabla p_P \cdot \bold{S}_f | ||
| + | </math> | ||
| + | |||
| + | and for the simplec method | ||
| + | |||
| + | <math> | ||
| + | (\bold {u_P} - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f = \underbrace{ (\frac{\bold {H[u^*] }}{a_P^* } - \bold{\Omega}\times \bold{R} - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1})\cdot \bold{S}_f}_{\text{phiHbyA}} - \underbrace{\frac{1}{a_P^* - H_1 }}_{ \text{rAtU}}\nabla p_P \cdot \bold{S}_f | ||
| + | </math> | ||
| + | |||
| + | Finally we rearrange for the pressure gradient, divide by the magnitude of the surface are vector <math> |\bold{S}_f| </math> and evaluate at the boundary we get (see also https://caefn.com/openfoam/solvers-recent-changes): | ||
| + | |||
| + | <math> | ||
| + | \nabla p_P \cdot \bold{n}_{bf} = \frac{1}{|\bold{S}_{bf} | \text{rAtU} } ( \text{phiHbyA} - (\bold {u_P} - \bold{\Omega}\times \bold{R})\cdot \bold{S}_{bf} ) | ||
| + | |||
| + | </math> | ||
| + | |||
| + | |||
| + | The source code can be found in $FOAM_SRC/finiteVolume/cfdTools/general/constrainPressure/constrainPressure.C: | ||
| + | |||
| + | <br><cpp> | ||
| + | |||
| + | template<class RAUType, class MRFType> | ||
| + | void Foam::constrainPressure | ||
| + | ( | ||
| + | volScalarField& p, | ||
| + | const volVectorField& U, | ||
| + | const surfaceScalarField& phiHbyA, | ||
| + | const RAUType& rAU, | ||
| + | const MRFType& MRF | ||
| + | ) | ||
| + | { | ||
| + | constrainPressure(p, geometricOneField(), U, phiHbyA, rAU, MRF); | ||
| + | } | ||
| + | |||
| + | template<class RhoType, class RAUType, class MRFType> | ||
| + | void Foam::constrainPressure | ||
| + | ( | ||
| + | volScalarField& p, | ||
| + | const RhoType& rho, | ||
| + | const volVectorField& U, | ||
| + | const surfaceScalarField& phiHbyA, | ||
| + | const RAUType& rhorAU, | ||
| + | const MRFType& MRF | ||
| + | ) | ||
| + | { | ||
| + | const fvMesh& mesh = p.mesh(); | ||
| + | |||
| + | volScalarField::Boundary& pBf = p.boundaryFieldRef(); | ||
| + | |||
| + | const volVectorField::Boundary& UBf = U.boundaryField(); | ||
| + | const surfaceScalarField::Boundary& phiHbyABf = | ||
| + | phiHbyA.boundaryField(); | ||
| + | const typename RAUType::Boundary& rhorAUBf = | ||
| + | rhorAU.boundaryField(); | ||
| + | const surfaceVectorField::Boundary& SfBf = | ||
| + | mesh.Sf().boundaryField(); | ||
| + | const surfaceScalarField::Boundary& magSfBf = | ||
| + | mesh.magSf().boundaryField(); | ||
| + | |||
| + | forAll(pBf, patchi) | ||
| + | { | ||
| + | if (isA<fixedFluxPressureFvPatchScalarField>(pBf[patchi])) | ||
| + | { | ||
| + | refCast<fixedFluxPressureFvPatchScalarField> | ||
| + | ( | ||
| + | pBf[patchi] | ||
| + | ).updateSnGrad | ||
| + | ( | ||
| + | ( | ||
| + | phiHbyABf[patchi] | ||
| + | - rho.boundaryField()[patchi] | ||
| + | *MRF.relative(SfBf[patchi] & UBf[patchi], patchi) | ||
| + | ) | ||
| + | /(magSfBf[patchi]*rhorAUBf[patchi]) | ||
| + | ); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | |||
| + | We see that fixedFluxPressure boundary condition sets the pressure gradient to the provided value such that the flux on the boundary is that specified by the velocity boundary condition. The pressure gradient is not set directly by the boundaryPatch but is set by the function constrainPressure which is called within the pressure equation. | ||
| + | |||
| + | In the next code snippet the pressure equation is solved. Furthermore a face flux <math> \phi_f </math> is generated which is consistent with the pressure equation solved. Note that a very good explanation of the flux operator in OF can be found in https://www.cfd-online.com/Forums/openfoam/114933-description-flux-method.html and is therefore not explained in detail. | ||
| + | |||
| + | The dot product <math> \nabla p_f \cdot \bold{S}_f </math> can be decomposed in following manner: <math> \nabla p_f \cdot \bold{S}_f = \nabla p_f \cdot \bold{E}_f + \nabla p_f \cdot \bold{T}_f </math> where the vector <math> \bold{E}_f </math> is pointing in direction of the two nodes straddling the face and the other one is perpendicular to this direction. The first term in the sum can be computed as function of the two cell center straddling the face and hence can be solved implicitly. The other therm can be written down only in a explicit manner (i.e. it is cast in the source term of the equation). For this reason we need a few iteration if the grid is highly non orthogonal. For details see <ref> Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016): </ref>. | ||
| + | |||
| + | <br><cpp> | ||
| + | // Non-orthogonal pressure corrector loop | ||
| + | while (simple.correctNonOrthogonal()) | ||
| + | { | ||
| + | fvScalarMatrix pEqn | ||
| + | ( | ||
| + | fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA) | ||
| + | ); | ||
| + | |||
| + | pEqn.setReference(pRefCell, pRefValue); | ||
| + | |||
| + | pEqn.solve(); | ||
| + | |||
| + | if (simple.finalNonOrthogonalIter()) | ||
| + | { | ||
| + | phi = phiHbyA - pEqn.flux(); | ||
| + | } | ||
| + | } | ||
| + | </cpp><br> | ||
| + | |||
| + | |||
| + | This file writes the continuity error on the screen. | ||
| + | |||
| + | <br><cpp> | ||
| + | #include "continuityErrs.H" | ||
| + | </cpp><br> | ||
| + | |||
| + | To stabilize the iterative method only a portion of the new pressure is used for the subsequent steps where <math> \alpha </math> is smaller than 1. | ||
| + | |||
| + | <math> | ||
| + | p^{n+1} = p^{n} + \alpha ( p^{n+1} - p^{n} ) | ||
| + | </math> | ||
| + | |||
| + | <br><cpp> | ||
| + | // Explicitly relax pressure for momentum corrector | ||
| + | p.relax(); | ||
| + | </cpp><br> | ||
| + | |||
| + | The source code can be found in $FOAM_SRC/OpenFOAM/fields/GeometricFields/GeometricField/GeometricField.C | ||
| + | |||
| + | <br><cpp> | ||
| + | template<class Type, template<class> class PatchField, class GeoMesh> | ||
| + | void Foam::GeometricField<Type, PatchField, GeoMesh>::relax(const scalar alpha) | ||
| + | { | ||
| + | DebugInFunction | ||
| + | << "Relaxing" << nl << this->info() << " by " << alpha << endl; | ||
| + | |||
| + | operator==(prevIter() + alpha*(*this - prevIter())); | ||
| + | } | ||
| + | </cpp><br> | ||
| + | |||
| + | For the simple method the velocity at point P con be written: | ||
| + | |||
| + | <math> | ||
| + | \bold {u_P} = \underbrace{\frac{\bold {H[u^*] }}{a_P^* }}_{\bold{HbyA}} - \underbrace{\frac{1}{a_P^* }}_{rAtU}\nabla p_P | ||
| + | </math> | ||
| + | |||
| + | For the simplec method the velocity obtains following expression: | ||
| + | |||
| + | <math> | ||
| + | \bold {u_P} = \underbrace{\frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1}}_{\bold{HbyA}} - \underbrace{\frac{1}{a_P^* - H_1 }}_{rAtU}\nabla p_P | ||
| + | </math> | ||
| + | |||
| + | We see from the above expression that the next code snippet is responsible for updating the velocity which is used as initial guess for the solution of the momentum equation in the next step momentum predictor step. | ||
| + | |||
| + | <br><cpp> | ||
// Momentum corrector | // Momentum corrector | ||
U = HbyA - rAtU()*fvc::grad(p); | U = HbyA - rAtU()*fvc::grad(p); | ||
| Line 609: | Line 1,111: | ||
\frac{\partial \left( \rho {u} u \right) }{\partial x}= -\frac{\partial p} {\partial{x}} | \frac{\partial \left( \rho {u} u \right) }{\partial x}= -\frac{\partial p} {\partial{x}} | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(16)</td></tr></table> |
The above equation is to be discretized on a equidistant grid: | The above equation is to be discretized on a equidistant grid: | ||
| Line 633: | Line 1,135: | ||
\sum_f \phi_f u_f = -\sum_f p_f S_f | \sum_f \phi_f u_f = -\sum_f p_f S_f | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(17)</td></tr></table> |
<math> \phi_f </math> is the phase flux and is computed from the previous iteration in order to resolve the non-linearity in the momentum equation. | <math> \phi_f </math> is the phase flux and is computed from the previous iteration in order to resolve the non-linearity in the momentum equation. | ||
| Line 642: | Line 1,144: | ||
\phi_e u_e - \phi_w u_w = - (p_e - p_w) \Delta y | \phi_e u_e - \phi_w u_w = - (p_e - p_w) \Delta y | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(18)</td></tr></table> |
With a central discretization of the velocity and pressure at the faces we obtain: | With a central discretization of the velocity and pressure at the faces we obtain: | ||
| Line 650: | Line 1,152: | ||
\phi_e \frac{1}{2} (u_P + u_E) - \phi_w \frac{1}{2} ( u_P + u_W) = - \left(\frac{1}{2}(p_P + p_E) - \frac{1}{2} (p_P + p_W) \right) \Delta y | \phi_e \frac{1}{2} (u_P + u_E) - \phi_w \frac{1}{2} ( u_P + u_W) = - \left(\frac{1}{2}(p_P + p_E) - \frac{1}{2} (p_P + p_W) \right) \Delta y | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(19)</td></tr></table> |
And finally: | And finally: | ||
| Line 657: | Line 1,159: | ||
<center><math> | <center><math> | ||
u_P \underbrace{ (\phi_e - \phi_w )}_{a_P} + \underbrace{u_E \phi_e - u_W \phi_w}_{\bold H[u]} = - \left ( p_E - p_W \right) \Delta y </math></center> | u_P \underbrace{ (\phi_e - \phi_w )}_{a_P} + \underbrace{u_E \phi_e - u_W \phi_w}_{\bold H[u]} = - \left ( p_E - p_W \right) \Delta y </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(20)</td></tr></table> |
It is evident that if no spatial care is taken and the face flux <math> \phi_f </math> is obtained by linear interpolation of the velocities | It is evident that if no spatial care is taken and the face flux <math> \phi_f </math> is obtained by linear interpolation of the velocities | ||
| Line 668: | Line 1,170: | ||
\phi_e = \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} | \phi_e = \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(21)</td></tr></table> |
<table width="70%"><tr><td> | <table width="70%"><tr><td> | ||
| Line 674: | Line 1,176: | ||
\phi_w = \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w} | \phi_w = \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w} | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(22)</td></tr></table> |
| Line 682: | Line 1,184: | ||
<center><math> | <center><math> | ||
u_P \left ( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} + \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) + u_E\left( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} \right ) - u_W \left ( \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) = - \left ( p_E - p_W \right) \Delta y </math></center> | u_P \left ( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} + \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) + u_E\left( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} \right ) - u_W \left ( \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) = - \left ( p_E - p_W \right) \Delta y </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(23)</td></tr></table> |
It evident that by correcting the face fluxes with the flux() operator of the fvMatrix class we obtain a dependency of the velocity at the centre point P from the pressure at the centre point P. Furthermore also the pressure and velocities at the neighbouring points E and W enter the momentum equation. | It evident that by correcting the face fluxes with the flux() operator of the fvMatrix class we obtain a dependency of the velocity at the centre point P from the pressure at the centre point P. Furthermore also the pressure and velocities at the neighbouring points E and W enter the momentum equation. | ||
| Line 692: | Line 1,194: | ||
\bold{ \frac{H[u^{*}]}{a_p}}|_e - \bold{ \frac{H[u^{*}]}{a_p}}|_w + \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | \bold{ \frac{H[u^{*}]}{a_p}}|_e - \bold{ \frac{H[u^{*}]}{a_p}}|_w + \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(24)</td></tr></table> |
After interpolating the H operator we get: | After interpolating the H operator we get: | ||
| Line 701: | Line 1,203: | ||
\frac{1}{2} \left ( \bold{ \frac{H[u^{*}]_E}{a_E}} - \bold{ \frac{H[u^{*}]_W}{a_W}} \right )+ \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | \frac{1}{2} \left ( \bold{ \frac{H[u^{*}]_E}{a_E}} - \bold{ \frac{H[u^{*}]_W}{a_W}} \right )+ \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(25)</td></tr></table> |
and finally: | and finally: | ||
| Line 709: | Line 1,211: | ||
\frac{1}{2} \left ( \frac{\phi_{ee}u^*_{EE}- \phi_e u^*_P }{\phi_{ee} - \phi_e} - \frac{\phi_{w}u^*_{P}- \phi_{ww} u^*_{WW} }{\phi_{w} - \phi_{ww}} \right )+ \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | \frac{1}{2} \left ( \frac{\phi_{ee}u^*_{EE}- \phi_e u^*_P }{\phi_{ee} - \phi_e} - \frac{\phi_{w}u^*_{P}- \phi_{ww} u^*_{WW} }{\phi_{w} - \phi_{ww}} \right )+ \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0 | ||
</math></center> | </math></center> | ||
| − | </td><td width="5%">( | + | </td><td width="5%">(26)</td></tr></table> |
From the above relation we can clearly see, that with a discretization of the Laplacian operator by interpolating the pressure gradients to the cell centre we would have a pressure stencil involving the points P, WW and EE. Since in the computation of the source term of the pressure equation we have the velocities stored at the points P, WW and EE we would have a complete decoupling of the neighbouring points in the pressure equation. This allows the existence of oscillatory solutions in the discrete case which are not part of the | From the above relation we can clearly see, that with a discretization of the Laplacian operator by interpolating the pressure gradients to the cell centre we would have a pressure stencil involving the points P, WW and EE. Since in the computation of the source term of the pressure equation we have the velocities stored at the points P, WW and EE we would have a complete decoupling of the neighbouring points in the pressure equation. This allows the existence of oscillatory solutions in the discrete case which are not part of the | ||
| Line 715: | Line 1,217: | ||
===Equations for the turbulence=== | ===Equations for the turbulence=== | ||
| + | The way the turbulent stresses enter into the momentum equation is well described here: https://www.openfoam.com/documentation/guides/latest/doc/guide-turbulence-ras.html. | ||
=References= | =References= | ||
<references/> | <references/> | ||
Latest revision as of 11:56, 16 September 2022
SimpleFoam
SimpleFoam is a steady-state solver for incompressible, turbulent flow, using the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm. In the newer releases it also includes an option to use the SIMPLEC (Semi-Implicit Method for Pressure Linked Equations Consistent) algorithm.
Contents
1 Solution Strategy
The solver follows a segregated solution strategy. This means that the equations for each variable characterizing the system (the velocity 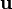 , the pressure
, the pressure 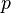 and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
 which is a function of the velocity) is resolved by computing it from the velocity and pressure values of the preceding iteration. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field
which is a function of the velocity) is resolved by computing it from the velocity and pressure values of the preceding iteration. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field  which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field
which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field  , which, if inserted in the momentum equation, delivers a divergence free velocity field
, which, if inserted in the momentum equation, delivers a divergence free velocity field 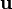 .
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
.
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
The source code can be found in simpleFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Copyright (C) 2011-2018 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application simpleFoam Description Steady-state solver for incompressible, turbulent flow, using the SIMPLE algorithm. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "singlePhaseTransportModel.H" #include "turbulentTransportModel.H" #include "simpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { #include "postProcess.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "initContinuityErrs.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (simple.loop(runTime)) { Info<< "Time = " << runTime.timeName() << nl << endl; // --- Pressure-velocity SIMPLE corrector { #include "UEqn.H" #include "pEqn.H" } laminarTransport.correct(); turbulence->correct(); runTime.write(); Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s" << " ClockTime = " << runTime.elapsedClockTime() << " s" << nl << endl; } Info<< "End\n" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Momentum Equation
The equation of motion in simpleFoam are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
-
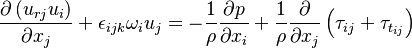 | (1) |
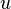 represent the absolute velocity,
represent the absolute velocity, 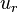 the relative veloicty,
the relative veloicty, 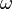 the angular velocity of the rotating fram
of reference and
the angular velocity of the rotating fram
of reference and
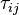 and
and 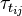 are the viscose and turbulent stresses. Not that in simpleFoam the momentum
equation solve, is divided by the constant density
are the viscose and turbulent stresses. Not that in simpleFoam the momentum
equation solve, is divided by the constant density 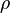 . Note that since the relative velocity
. Note that since the relative velocity 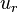 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux  appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
The source code can be found in UEqn.H:
// Momentum predictor
MRF.correctBoundaryVelocity(U);
tmp<fvVectorMatrix> tUEqn
(
fvm::div(phi, U)
+ MRF.DDt(U)
+ turbulence->divDevReff(U)
==
fvOptions(U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
UEqn.relax();
fvOptions.constrain(UEqn);
if (simple.momentumPredictor())
{
solve(UEqn == -fvc::grad(p));
fvOptions.correct(U);
}
The source code of the acceleration resulting from the description in a moving frame of reference can be found in the following src/finiteVolume/cfdTools/general/MRF/MRFZoneList.C
Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt ( const volVectorField& U ) const { tmp<volVectorField> tacceleration ( new volVectorField ( IOobject ( "MRFZoneList:acceleration", U.mesh().time().timeName(), U.mesh() ), U.mesh(), dimensionedVector(U.dimensions()/dimTime, Zero) ) ); volVectorField& acceleration = tacceleration.ref(); forAll(*this, i) { operator[](i).addCoriolis(U, acceleration); } return tacceleration; }
The calculation of the Coriolis force is done in the file src/finiteVolume/cfdTools/general/MRF/MRFZone.C
void Foam::MRFZone::addCoriolis ( const volVectorField& U, volVectorField& ddtU ) const { if (cellZoneID_ == -1) { return; } const labelList& cells = mesh_.cellZones()[cellZoneID_]; vectorField& ddtUc = ddtU.primitiveFieldRef(); const vectorField& Uc = U; const vector Omega = this->Omega(); forAll(cells, i) { label celli = cells[i]; ddtUc[celli] += (Omega ^ Uc[celli]); } }
In the following the numeric used to solve the momentum equation are briefly explained.
The first step performed is to assemble the matrix which is later solved to obtain the estimate of the velocity  :
:
tmp<fvVectorMatrix> tUEqn
(
fvm::div(phi, U)
+ MRF.DDt(U)
+ turbulence->divDevReff(U)
==
fvOptions(U)
);
In the usual semi discrete form it can be written as (see also [1]. ):
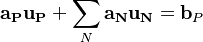 | (2) |
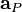 are the matrix coefficient associated with the centre point P,
are the matrix coefficient associated with the centre point P, 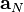 the matrix coefficients associated with all neighbours influencing the computational stencil around point P and
the matrix coefficients associated with all neighbours influencing the computational stencil around point P and 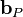 is the source therm. The sum
is the source therm. The sum 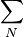 is taken over all neighbours influencing the computational stencil around point P.
is taken over all neighbours influencing the computational stencil around point P.
The next step performed is the under relax the equation:
UEqn.relax();
The under relaxation is required in order to prevent the solution to diverge. Even though the discrete equation of the momentum
equation is linear, the non linearity is resolve by using the solution of the previous iteration. This causes a large change of the new velocity leading often to divergence [2]. Using Patankar's implicit under relaxation the new semi discrete momentum equation can be written as:
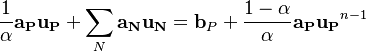 | (3) |
Here  denotes the under relaxation factor and
denotes the under relaxation factor and  denotes the solution at the previous iteration step.
The source code for the under relaxation can be found in fvMatrix.C (see also https://www.openfoam.com/documentation/cpp-guide/html/fvMatrix_8C_source.html):
denotes the solution at the previous iteration step.
The source code for the under relaxation can be found in fvMatrix.C (see also https://www.openfoam.com/documentation/cpp-guide/html/fvMatrix_8C_source.html):
template<class Type> void Foam::fvMatrix<Type>::relax(const scalar alpha) { if (alpha <= 0) { return; } if (debug) { InfoInFunction << "Relaxing " << psi_.name() << " by " << alpha << endl; } Field<Type>& S = source(); scalarField& D = diag(); // Store the current unrelaxed diagonal for use in updating the source scalarField D0(D); // Calculate the sum-mag off-diagonal from the interior faces scalarField sumOff(D.size(), 0.0); sumMagOffDiag(sumOff); // Handle the boundary contributions to the diagonal forAll(psi_.boundaryField(), patchi) { const fvPatchField<Type>& ptf = psi_.boundaryField()[patchi]; if (ptf.size()) { const labelUList& pa = lduAddr().patchAddr(patchi); Field<Type>& iCoeffs = internalCoeffs_[patchi]; if (ptf.coupled()) { const Field<Type>& pCoeffs = boundaryCoeffs_[patchi]; // For coupled boundaries add the diagonal and // off-diagonal contributions forAll(pa, face) { D[pa[face]] += component(iCoeffs[face], 0); sumOff[pa[face]] += mag(component(pCoeffs[face], 0)); } } else { // For non-coupled boundaries add the maximum magnitude diagonal // contribution to ensure stability forAll(pa, face) { D[pa[face]] += cmptMax(cmptMag(iCoeffs[face])); } } } } if (debug) { // Calculate amount of non-dominance. label nNon = 0; scalar maxNon = 0.0; scalar sumNon = 0.0; forAll(D, celli) { scalar d = (sumOff[celli] - D[celli])/mag(D[celli]); if (d > 0) { nNon++; maxNon = max(maxNon, d); sumNon += d; } } reduce(nNon, sumOp<label>(), UPstream::msgType(), psi_.mesh().comm()); reduce ( maxNon, maxOp<scalar>(), UPstream::msgType(), psi_.mesh().comm() ); reduce ( sumNon, sumOp<scalar>(), UPstream::msgType(), psi_.mesh().comm() ); sumNon /= returnReduce ( D.size(), sumOp<label>(), UPstream::msgType(), psi_.mesh().comm() ); InfoInFunction << "Matrix dominance test for " << psi_.name() << nl << " number of non-dominant cells : " << nNon << nl << " maximum relative non-dominance : " << maxNon << nl << " average relative non-dominance : " << sumNon << nl << endl; } // Ensure the matrix is diagonally dominant... // Assumes that the central coefficient is positive and ensures it is forAll(D, celli) { D[celli] = max(mag(D[celli]), sumOff[celli]); } // ... then relax D /= alpha; // Now remove the diagonal contribution from coupled boundaries forAll(psi_.boundaryField(), patchi) { const fvPatchField<Type>& ptf = psi_.boundaryField()[patchi]; if (ptf.size()) { const labelUList& pa = lduAddr().patchAddr(patchi); Field<Type>& iCoeffs = internalCoeffs_[patchi]; if (ptf.coupled()) { forAll(pa, face) { D[pa[face]] -= component(iCoeffs[face], 0); } } else { forAll(pa, face) { D[pa[face]] -= cmptMin(iCoeffs[face]); } } } } // Finally add the relaxation contribution to the source. S += (D - D0)*psi_.primitiveField(); }
After the under relaxation the contribution of the pressure gradient is added to the right hand side of the matrix and the system is solve:
solve(UEqn == -fvc::grad(p));The equation in semi discrete form looks as follows:
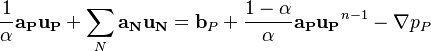 | (4) |
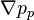 denotes the contribution of the pressure gradient to the equation of the cell centre p. It depends on the scheme
chosen to discretize the gradient operator.
denotes the contribution of the pressure gradient to the equation of the cell centre p. It depends on the scheme
chosen to discretize the gradient operator.
Important for the understanding of the later described pressure equation is that the contribution of the pressure equation is not added to the source therm of the
matrix object UEqn. Rather a new fvMatrix object is returned by the call of the overloaded operator == to the function solve:
UEqn == -fvc::grad(p)The function solve is then executed, which solves the new fvMatrix object in order to obtain the estimate  by also considering the contribution
of the pressure equation. Note that the the volVectorField U is modified by solving the matrix since the solution vector
by also considering the contribution
of the pressure equation. Note that the the volVectorField U is modified by solving the matrix since the solution vector  of the matrix is a reference to U.
An explanation of the the implementation can be found also in https://www.cfd-online.com/Forums/openfoam/213566-why-solve-ueqn-fvc-grad-p-ueqn-source-not-modified-ueqn-h-chang.html.
of the matrix is a reference to U.
An explanation of the the implementation can be found also in https://www.cfd-online.com/Forums/openfoam/213566-why-solve-ueqn-fvc-grad-p-ueqn-source-not-modified-ueqn-h-chang.html.
2.2 Pressure Equation
In this section the pressure equation solved in simpleFoam in order to ensure the mass conservation is derived. A good explanation of the derivation of the SIMPLE and also SIMPLEC method in simpleFoam can be found also in http://hobbyfoam.blogspot.com/2016/01/simplec-algorithm-of-openfoam.html.
Starting point for the derivation of the pressure equation is the momentum equation in semi discrete form after the solution of the momentum equation:
![\bold{a_P^* u_P^*} = - \sum_{N} \bold{a_N u_N^*} + \bold b_P + \frac{1 - \alpha}{\alpha}\bold{a_P u_P}^{n-1} - \nabla p_P^{n-1} = \bold {H[u^*] } - \nabla p_P^{n-1}](/images/math/8/f/7/8f791b1e0084e9353ec263e764f5105f.png) | (5) |
After dividing the above equation by 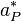 we obtain:
we obtain:
![\bold{u_P^*} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* }](/images/math/2/2/2/2223c388faf5c26d534ecdf3784b4fcd.png) | (6) |
Note that according to https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse the continuity equation is the same for the relative velocity described in a reference frame subject to a rigid body motion and the velocity described in an inertial frame of
reference. For that reason the following equation are valid for the relative velocity 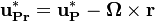 and also the absolute velocity
and also the absolute velocity 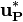 .
. 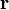 is the vector from the center of rotation to the position of interest. For this reason we get the equations solve in the case of a moving reference frame simply by adding the term
is the vector from the center of rotation to the position of interest. For this reason we get the equations solve in the case of a moving reference frame simply by adding the term 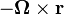 on both sides of equation (6) and continue with the same procedure as described in the following.
on both sides of equation (6) and continue with the same procedure as described in the following.
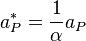 are the modified diagonal coefficients of the matrix after the under relaxation.
are the modified diagonal coefficients of the matrix after the under relaxation.
The scope of the next step is to find a
correction for the velocity 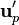 and for the pressure
and for the pressure 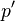 in order to find a velocity
in order to find a velocity 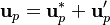 which satisfies the continuum equation:
which satisfies the continuum equation:
![\bold{u_P} = \frac{\bold {H[u^*] }}{a_P^* } + \frac{\bold {H[u'] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{\nabla p_P'}{a_P^* }](/images/math/5/3/a/53ab94578af9b549bc699e92c5e8ef47.png) | (7) |
The equation for the velocity correction can be written as:
![\bold{u_P'} = - \frac{\sum_{N} \bold{a_N u_N'}}{a_P^* } - \frac{\nabla p_P'}{a_P^* } = \frac{\bold {H[u'] }}{a_P^* } - \frac{\nabla p_P'}{a_P^* }](/images/math/7/5/9/759f8d7415144e5b8678749bbfdce3a5.png) | (8) |
Note that here it is assumed that the diagonal coefficients of the corrector equation are the same as in the momentum equation previously solved.
Taking the divergence of the above equation and setting it to zero (we want to obtain a velocity field 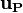 which satisfies the continuity
equation) we get an equation for the pressure
which satisfies the continuity
equation) we get an equation for the pressure 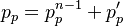 :
:
![\sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f + \sum_f \frac{\bold {H[u'] }}{a_P^* }|_f \cdot S_f - \sum_f \frac{\nabla p_P}{a_P^* }|_f \cdot S_f = 0](/images/math/3/2/8/3284224e494c25922589134533306b0d.png) | (9) |
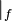 denotes the values evaluated at the face.
denotes the values evaluated at the face.
2.2.1 Simple
If we neglect the contribution of the neighbours of the velocity correction (i.e. we set ![\bold {H[u'] } = 0](/images/math/4/8/c/48c782a087e13ca25277df5340ac0323.png) ) we get the pressure equation solved in the simplec
algorithm:
) we get the pressure equation solved in the simplec
algorithm:
![\sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f - \sum_f \frac{\nabla p_P}{a_P^* }|_f \cdot S_f = 0](/images/math/1/b/2/1b221a989c1d546f1a5415b871ca42f8.png) | (10) |
The source code can be found in pEqn.H:
{ volScalarField rAU(1.0/UEqn.A()); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA)); MRF.makeRelative(phiHbyA); adjustPhi(phiHbyA, U, p); tmp<volScalarField> rAtU(rAU); if (simple.consistent()) { rAtU = 1.0/(1.0/rAU - UEqn.H1()); phiHbyA += fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf(); HbyA -= (rAU - rAtU())*fvc::grad(p); } tUEqn.clear(); // Update the pressure BCs to ensure flux consistency constrainPressure(p, U, phiHbyA, rAtU(), MRF); // Non-orthogonal pressure corrector loop while (simple.correctNonOrthogonal()) { fvScalarMatrix pEqn ( fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA) ); pEqn.setReference(pRefCell, pRefValue); pEqn.solve(); if (simple.finalNonOrthogonalIter()) { phi = phiHbyA - pEqn.flux(); } } #include "continuityErrs.H" // Explicitly relax pressure for momentum corrector p.relax(); // Momentum corrector U = HbyA - rAtU()*fvc::grad(p); U.correctBoundaryConditions(); fvOptions.correct(U); }
2.2.2 Simplec
The starting point for the simplec algorithm is the equation for the velocity correction. The goal is the obtain a simplification to get an explicit relation for the velocity correction and hence avoiding to solve a matrix equation:
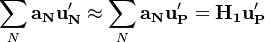 | (11) |
Inserting the above approximation into the equation for the velocity correction we get:
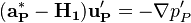 | (12) |
Solving for the velocity correction:
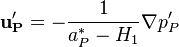 | (13) |
The above equation formulates an explicit relation between velocity correction and pressure correction. In the next step we write down:
![\bold {u_P^*} + \bold{ u_P'} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{1}{a_P^* - H_1 }\nabla p_P' = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} - \frac{1}{a_P^* - H_1 }\nabla p_P](/images/math/0/3/3/0335d6bd01f41d99b0c0c544d5f073c2.png) | (14) |
By taking the divergence of the above equation and setting it to zero we obtain the pressure equation for the simplec algorithm:
![\sum_f \frac{\bold {H[u^*] }}{a_P^* }|_f \cdot S_f - \sum_f \left ( \frac{1}{a_P^*} |_f - \frac{1}{a_P^* |_f - H_1 |_f } \right )\nabla p_P^{n-1} |_f \cdot S_f - \sum_f \frac{1}{a_P^* - H_1 }\nabla p_P |_f \cdot S_f = 0](/images/math/0/2/9/0295b67e1496498a9c4c8fafa8ad6b07.png) | (15) |
The difference between the pressure equation in the SIMPLE and SIMPLEC consists only in one term.
The source code for the pressure equation can be seen here:
volScalarField rAU(1.0/UEqn.A());
volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA));
MRF.makeRelative(phiHbyA);
adjustPhi(phiHbyA, U, p);
tmp<volScalarField> rAtU(rAU);
if (simple.consistent())
{
rAtU = 1.0/(1.0/rAU - UEqn.H1());
phiHbyA +=
fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf();
HbyA -= (rAU - rAtU())*fvc::grad(p);
}
tUEqn.clear();
// Update the pressure BCs to ensure flux consistency
constrainPressure(p, U, phiHbyA, rAtU(), MRF);
// Non-orthogonal pressure corrector loop
while (simple.correctNonOrthogonal())
{
fvScalarMatrix pEqn
(
fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA)
);
pEqn.setReference(pRefCell, pRefValue);
pEqn.solve();
if (simple.finalNonOrthogonalIter())
{
phi = phiHbyA - pEqn.flux();
}
}
#include "continuityErrs.H"
// Explicitly relax pressure for momentum corrector
p.relax();
// Momentum corrector
U = HbyA - rAtU()*fvc::grad(p);
U.correctBoundaryConditions();
fvOptions.correct(U);
}
2.2.3 Step by step analysis of the pressure equation
In this section we will analyze step by step the pressure equation since this source code does not solve only the pressure equation but executes also the corrector step for the velocity (which is used as initial guess for the solution of the momentum equation in the next iteration step) and for the face flux 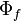 which is used to discretize the convective terms in the momentum equation.
which is used to discretize the convective terms in the momentum equation.
volScalarField rAU(1.0/UEqn.A());This line computes the field of diagonal entries of the momentum equation required later on to solve the pressure equation:
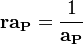
Since the reciprocal of the diagonal is required a few times, the division is done once and then it is multiplied where required. This is done since the multiplication are computationally cheaper than the division.
volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));The source code can be found in the file $FOAM_SCR/finiteVolume/cfdTools/general/constrainHbyA/constrainHbyA.C
Foam::tmp<Foam::volVectorField> Foam::constrainHbyA ( const tmp<volVectorField>& tHbyA, const volVectorField& U, const volScalarField& p ) { tmp<volVectorField> tHbyANew; if (tHbyA.isTmp()) { tHbyANew = tHbyA; tHbyANew.ref().rename("HbyA"); } else { tHbyANew = new volVectorField("HbyA", tHbyA); } volVectorField& HbyA = tHbyANew.ref(); volVectorField::Boundary& HbyAbf = HbyA.boundaryFieldRef(); forAll(U.boundaryField(), patchi) { if ( !U.boundaryField()[patchi].assignable() && !isA<fixedFluxExtrapolatedPressureFvPatchScalarField> ( p.boundaryField()[patchi] ) ) { HbyAbf[patchi] = U.boundaryField()[patchi]; } } return tHbyANew; }
The velocity at the boundary face should satisfy following equation:
![\bold{u}|_{bf} = \frac{\bold {H[u] }}{a_P }|_{bf} - \frac{\nabla p{}}{a_P }|_{bf}](/images/math/2/5/b/25be70ff25adbc4c8fec5e3f27875b22.png) |
The subscript bf denoted that the quantity is evaluated at the boundary face. The function constrainHbyA ensures that the field ![\frac{\bold {H[u] }}{a_P }|_{bf}](/images/math/f/2/0/f209495cf47c9c939e5083c0c7bfa316.png) does not violate the above equation. The boundary condition fixedFluxExtrapolatedPressure sets the pressure gradient in order that the above equation is satisfied. If we cannot modify the velocity, the function sets the field
does not violate the above equation. The boundary condition fixedFluxExtrapolatedPressure sets the pressure gradient in order that the above equation is satisfied. If we cannot modify the velocity, the function sets the field ![\frac{\bold {H[u] }}{a_P }|_{bf} = \bold{u}|_{bf}](/images/math/3/7/3/3737d1c8db22f2ad1fc57aa13458762b.png) in order that the field
in order that the field ![\frac{\bold {H[u] }}{a_P }|_{bf}](/images/math/f/2/0/f209495cf47c9c939e5083c0c7bfa316.png) does not contradict the zero gradient boundary condition which should be applied for the pressure if the velocity is fixed.
does not contradict the zero gradient boundary condition which should be applied for the pressure if the velocity is fixed.
surfaceScalarField phiHbyA("phiHbyA", fvc::flux(HbyA));The above function performs the following operation:
![\Phi H = \frac{\bold {H[u] }}{a_P }\cdot S_f|_{f}](/images/math/b/b/7/bb7d17f542ee87afea97686844f4eb13.png)
It interpolates the field ![\frac{\bold {H[u] }}{a_P }](/images/math/3/2/b/32b0e6c4334c895e91202752da18e56b.png) at the cell faces and makes than the scalar product of the interpolated field with the surface vector
at the cell faces and makes than the scalar product of the interpolated field with the surface vector 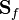 . The source can be found in $FOAM_SCR/finiteVolume/finiteVolume/fvc/fvcFlux.C
. The source can be found in $FOAM_SCR/finiteVolume/finiteVolume/fvc/fvcFlux.C
Foam::tmp<Foam::surfaceScalarField> Foam::fvc::flux ( const volVectorField& vvf ) { return scheme<vector> ( vvf.mesh(), "flux(" + vvf.name() + ')' )().dotInterpolate(vvf.mesh().Sf(), vvf); }
In a grid which is not deforming and moves with a moving frame of reference the continuity equation has to be satisfied within this grid. This means that the sum of the relative fluxes over the control volumes have to be zero:
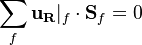
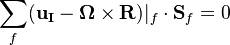
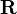 is the vector pointing from the origin of the rotation to the face center.
is the vector pointing from the origin of the rotation to the face center.
MRF.makeRelative(phiHbyA);
The source code can be found in $FOAM_SCR/cfdTools/general/MRF/MRFZoneTemplates.C and $FOAM_SCR/cfdTools/general/MRF/MRFZone.C
void Foam::MRFZone::makeRelative(surfaceScalarField& phi) const { makeRelativeRhoFlux(geometricOneField(), phi); } template<class RhoFieldType> void Foam::MRFZone::makeRelativeRhoFlux ( const RhoFieldType& rho, surfaceScalarField& phi ) const { if (!active_) { return; } const surfaceVectorField& Cf = mesh_.Cf(); const surfaceVectorField& Sf = mesh_.Sf(); const vector Omega = omega_->value(mesh_.time().timeOutputValue())*axis_; const vectorField& Cfi = Cf; const vectorField& Sfi = Sf; scalarField& phii = phi.primitiveFieldRef(); // Internal faces forAll(internalFaces_, i) { label facei = internalFaces_[i]; phii[facei] -= rho[facei]*(Omega ^ (Cfi[facei] - origin_)) & Sfi[facei]; } makeRelativeRhoFlux(rho.boundaryField(), phi.boundaryFieldRef()); }
This call ensures that the global mass balance is satisfied if one sets a refence pressure. For more details see the thread https://www.cfd-online.com/Forums/openfoam-programming-development/83876-pref-adjustphi.html.
adjustPhi(phiHbyA, U, p);
tmp<volScalarField> rAtU(rAU);This if condition computes the fields required for the simplec method.
Furthermore it already adds the velocity correction to the field HbyA.
![\bold{HbyA} = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1}](/images/math/3/a/6/3a69f20deee5bc3855befe965f298333.png)
This field is later used to compute the corrected velocity to be used as initial condition for the next iteration of the momentum equation.
if (simple.consistent())
{
rAtU = 1.0/(1.0/rAU - UEqn.H1());
phiHbyA +=
fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.magSf();
HbyA -= (rAU - rAtU())*fvc::grad(p);
}
tUEqn.clear();This function updates the pressure gradient for the patches where a fixedFluxPressure boundary condition is chosen
// Update the pressure BCs to ensure flux consistency
constrainPressure(p, U, phiHbyA, rAtU(), MRF);For the simple method the velocity at point P con be written:
![\bold {u_P} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{1}{a_P^* }\nabla p_P](/images/math/d/e/3/de3a30884b42aa6b60490dbde9fccadc.png)
For the simplec method the velocity obtains following expression:
![\bold {u_P} = \frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1} - \frac{1}{a_P^* - H_1 }\nabla p_P](/images/math/5/2/5/525a2224de3ed8a363a5d29ee7d3420b.png)
If we add 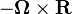 to the above expression and make the dot product with the surface are vector
to the above expression and make the dot product with the surface are vector 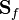 we get for the simple method
we get for the simple method
![(\bold {u_P} - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f = \underbrace{ (\frac{\bold {H[u^*] }}{a_P^* } - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f}_{\text{phiHbyA}} - \underbrace{\frac{1}{a_P^* }}_{\text{ rAtU}}\nabla p_P \cdot \bold{S}_f](/images/math/f/a/9/fa9f1b62915829ffc6f783e29647a686.png)
and for the simplec method
![(\bold {u_P} - \bold{\Omega}\times \bold{R})\cdot \bold{S}_f = \underbrace{ (\frac{\bold {H[u^*] }}{a_P^* } - \bold{\Omega}\times \bold{R} - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1})\cdot \bold{S}_f}_{\text{phiHbyA}} - \underbrace{\frac{1}{a_P^* - H_1 }}_{ \text{rAtU}}\nabla p_P \cdot \bold{S}_f](/images/math/3/e/1/3e1d5bcc46a4c4c7c73aa0fb3b8c02f4.png)
Finally we rearrange for the pressure gradient, divide by the magnitude of the surface are vector 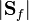 and evaluate at the boundary we get (see also https://caefn.com/openfoam/solvers-recent-changes):
and evaluate at the boundary we get (see also https://caefn.com/openfoam/solvers-recent-changes):
The source code can be found in $FOAM_SRC/finiteVolume/cfdTools/general/constrainPressure/constrainPressure.C:
template<class RAUType, class MRFType> void Foam::constrainPressure ( volScalarField& p, const volVectorField& U, const surfaceScalarField& phiHbyA, const RAUType& rAU, const MRFType& MRF ) { constrainPressure(p, geometricOneField(), U, phiHbyA, rAU, MRF); } template<class RhoType, class RAUType, class MRFType> void Foam::constrainPressure ( volScalarField& p, const RhoType& rho, const volVectorField& U, const surfaceScalarField& phiHbyA, const RAUType& rhorAU, const MRFType& MRF ) { const fvMesh& mesh = p.mesh(); volScalarField::Boundary& pBf = p.boundaryFieldRef(); const volVectorField::Boundary& UBf = U.boundaryField(); const surfaceScalarField::Boundary& phiHbyABf = phiHbyA.boundaryField(); const typename RAUType::Boundary& rhorAUBf = rhorAU.boundaryField(); const surfaceVectorField::Boundary& SfBf = mesh.Sf().boundaryField(); const surfaceScalarField::Boundary& magSfBf = mesh.magSf().boundaryField(); forAll(pBf, patchi) { if (isA<fixedFluxPressureFvPatchScalarField>(pBf[patchi])) { refCast<fixedFluxPressureFvPatchScalarField> ( pBf[patchi] ).updateSnGrad ( ( phiHbyABf[patchi] - rho.boundaryField()[patchi] *MRF.relative(SfBf[patchi] & UBf[patchi], patchi) ) /(magSfBf[patchi]*rhorAUBf[patchi]) ); } } }
We see that fixedFluxPressure boundary condition sets the pressure gradient to the provided value such that the flux on the boundary is that specified by the velocity boundary condition. The pressure gradient is not set directly by the boundaryPatch but is set by the function constrainPressure which is called within the pressure equation.
In the next code snippet the pressure equation is solved. Furthermore a face flux  is generated which is consistent with the pressure equation solved. Note that a very good explanation of the flux operator in OF can be found in https://www.cfd-online.com/Forums/openfoam/114933-description-flux-method.html and is therefore not explained in detail.
is generated which is consistent with the pressure equation solved. Note that a very good explanation of the flux operator in OF can be found in https://www.cfd-online.com/Forums/openfoam/114933-description-flux-method.html and is therefore not explained in detail.
The dot product 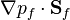 can be decomposed in following manner:
can be decomposed in following manner: 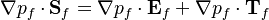 where the vector
where the vector 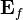 is pointing in direction of the two nodes straddling the face and the other one is perpendicular to this direction. The first term in the sum can be computed as function of the two cell center straddling the face and hence can be solved implicitly. The other therm can be written down only in a explicit manner (i.e. it is cast in the source term of the equation). For this reason we need a few iteration if the grid is highly non orthogonal. For details see [3].
is pointing in direction of the two nodes straddling the face and the other one is perpendicular to this direction. The first term in the sum can be computed as function of the two cell center straddling the face and hence can be solved implicitly. The other therm can be written down only in a explicit manner (i.e. it is cast in the source term of the equation). For this reason we need a few iteration if the grid is highly non orthogonal. For details see [3].
// Non-orthogonal pressure corrector loop
while (simple.correctNonOrthogonal())
{
fvScalarMatrix pEqn
(
fvm::laplacian(rAtU(), p) == fvc::div(phiHbyA)
);
pEqn.setReference(pRefCell, pRefValue);
pEqn.solve();
if (simple.finalNonOrthogonalIter())
{
phi = phiHbyA - pEqn.flux();
}
}
This file writes the continuity error on the screen.
#include "continuityErrs.H"To stabilize the iterative method only a portion of the new pressure is used for the subsequent steps where 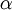 is smaller than 1.
is smaller than 1.
// Explicitly relax pressure for momentum corrector
p.relax();The source code can be found in $FOAM_SRC/OpenFOAM/fields/GeometricFields/GeometricField/GeometricField.C
template<class Type, template<class> class PatchField, class GeoMesh> void Foam::GeometricField<Type, PatchField, GeoMesh>::relax(const scalar alpha) { DebugInFunction << "Relaxing" << nl << this->info() << " by " << alpha << endl; operator==(prevIter() + alpha*(*this - prevIter())); }
For the simple method the velocity at point P con be written:
![\bold {u_P} = \underbrace{\frac{\bold {H[u^*] }}{a_P^* }}_{\bold{HbyA}} - \underbrace{\frac{1}{a_P^* }}_{rAtU}\nabla p_P](/images/math/5/7/6/5769ab5f9a60d4f16bc696b486e6f29e.png)
For the simplec method the velocity obtains following expression:
![\bold {u_P} = \underbrace{\frac{\bold {H[u^*] }}{a_P^* } - \left ( \frac{1}{a_P^*} - \frac{1}{a_P^* - H_1 } \right )\nabla p_P^{n-1}}_{\bold{HbyA}} - \underbrace{\frac{1}{a_P^* - H_1 }}_{rAtU}\nabla p_P](/images/math/0/7/b/07b61ca2ecfb05fbae4a6b1e4afdc7be.png)
We see from the above expression that the next code snippet is responsible for updating the velocity which is used as initial guess for the solution of the momentum equation in the next step momentum predictor step.
// Momentum corrector
U = HbyA - rAtU()*fvc::grad(p);
U.correctBoundaryConditions();
fvOptions.correct(U);
}
2.3 Avoiding checker boarder effects
The usual way to avoid the so called "checker board" effect is to interpolate the velocities at the faces by means of the Rhie and Chow interpolation (see e.g. [4] or [5]. ) . The checker board effect has its origin in the absence of neighbouring pressure terms in the momentum equation due to the discretization of the pressure gradient term in the frame of the finite volume method using a collocated variable arrangement. The same absence of neighbouring pressure terms is obtained when the Laplacian term is discretized by linear interpolation of the pressure gradient on the face centres. In the implementation of the simpleFoam solver, the Rhie and Chow interpolation is not done in an explicit way. The introduction of neighbour pressure terms in the momentum and pressure equation is done in the spirit of Rhie and Chow [6] . It is achieved by two contribution: The first one is the way the Laplacian term is disretized (see also http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2007/rhiechow.pdf). The second contribution is achieved by the flux() operator after the solution of the pressure equation:
if (simple.finalNonOrthogonalIter())
{
phi = phiHbyA - pEqn.flux();
}The principle of how the pressure oscillations are avoided in simpleFoam are explained by means of a simple 1D convection equation:
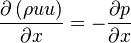 | (16) |
The above equation is to be discretized on a equidistant grid:
----------------------------------------------------------------------------------------------------------------------------- | | | | | | | | | | | | | WW |ww W |w P e| E ee | EE | | | | | | | | | | | | | -----------------------------------------------------------------------------------------------------------------------------
The usual geographic notation is adoped to describe the discretization stencil around the point P for which the solution has to be obtained.
The discretization with a finite volume method leads to the following equation:
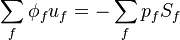 | (17) |
 is the phase flux and is computed from the previous iteration in order to resolve the non-linearity in the momentum equation.
Evaluating the above sum for the central point P we get:
is the phase flux and is computed from the previous iteration in order to resolve the non-linearity in the momentum equation.
Evaluating the above sum for the central point P we get:
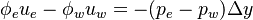 | (18) |
With a central discretization of the velocity and pressure at the faces we obtain:
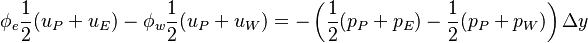 | (19) |
And finally:
![u_P \underbrace{ (\phi_e - \phi_w )}_{a_P} + \underbrace{u_E \phi_e - u_W \phi_w}_{\bold H[u]} = - \left ( p_E - p_W \right) \Delta y](/images/math/d/a/5/da51a8a016cd9386b28ced053f45269f.png) | (20) |
It is evident that if no spatial care is taken and the face flux  is obtained by linear interpolation of the velocities
the velocity at the cell center P is not coupled with the pressure at P but only at the neighboring points E and W. The diagonal coefficient
is obtained by linear interpolation of the velocities
the velocity at the cell center P is not coupled with the pressure at P but only at the neighboring points E and W. The diagonal coefficient  are in this case
are in this case  and the contributions of the neighbor cells
and the contributions of the neighbor cells ![\bold H[u]](/images/math/1/3/e/13e8da14f112f41cdf7bfe362c5a82a2.png) are
are ![\bold H[u] = u_E \phi_e - u_W \phi_w](/images/math/8/f/c/8fcf2d598a004c8979ca98e95c342d39.png) .
.
In order to understand how the pressure at the cell centre P is cast into the momentum equation it is important to understand how the flux() operator is defined in the fvMatrix class. Note that a very good description can be found in https://www.cfd-online.com/Forums/openfoam/114933-description-flux-method.html. Using the implementation of the flux operator we get the new fluxes at the faces for this example:
![\phi_e = \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e}](/images/math/0/8/1/081a2950da5e940e28012caf7630608f.png) | (21) |
![\phi_w = \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w}](/images/math/2/9/7/297776692796d4a1d1a9bba5121f371a.png) | (22) |
Note that the quantities denoted with  denote the quantities at the previous iteration and
denote the quantities at the previous iteration and 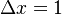 in this illustriously example. Note also that the pressure used to correct the face fluxes come from the solution of the pressure equation. After inserting the two above relations for the phase fluxes on the east and west side of the cell centre in the momentum equation we get:
in this illustriously example. Note also that the pressure used to correct the face fluxes come from the solution of the pressure equation. After inserting the two above relations for the phase fluxes on the east and west side of the cell centre in the momentum equation we get:
![u_P \left ( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} + \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) + u_E\left( \bold{ \frac{H[u^{-}]}{a_p^-}}|_e - \frac{p_P - p_E}{\Delta x \bold a_P^-|e} \right ) - u_W \left ( \bold{ \frac{H[u^-]}{a_p^-}}|_w - \frac{p_W - p_P}{\Delta x \bold a_P^-|w} \right ) = - \left ( p_E - p_W \right) \Delta y](/images/math/1/0/6/106d7f9c56f69273d6f318d1ed4c0135.png) | (23) |
It evident that by correcting the face fluxes with the flux() operator of the fvMatrix class we obtain a dependency of the velocity at the centre point P from the pressure at the centre point P. Furthermore also the pressure and velocities at the neighbouring points E and W enter the momentum equation.
The second measure undertaken to avoid a decoupling of the pressure at neighbouring points is achieved by the way the Laplacian operator is discretized: It computes the gradient at the cell faces by computing the difference between neighbour and owner cell centre and dividing this difference by the distance between this two points. In this way when the sum of all gradients is taken over the faces of a cell, the computational stencil is much smaller compared with the procedure to interpolated the gradient computed at the cell centre on the faces. Furthermore it involves direct neighbours without alternately skipping neighbours. In this way we obtain the following pressure equation for our simple example:
![\bold{ \frac{H[u^{*}]}{a_p}}|_e - \bold{ \frac{H[u^{*}]}{a_p}}|_w + \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0](/images/math/8/e/0/8e09c563e13f57582630f5cd8a873a6e.png) | (24) |
After interpolating the H operator we get:
![\frac{1}{2} \left ( \bold{ \frac{H[u^{*}]_E}{a_E}} - \bold{ \frac{H[u^{*}]_W}{a_W}} \right )+ \frac{p_E - p_P}{\Delta x \bold a_P|e} - \frac{p_P - p_W}{\Delta x \bold a_P|w} = 0](/images/math/c/4/b/c4be0eb8a60f47480bd887df2f9134e8.png) | (25) |
and finally:
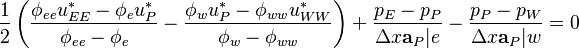 | (26) |
From the above relation we can clearly see, that with a discretization of the Laplacian operator by interpolating the pressure gradients to the cell centre we would have a pressure stencil involving the points P, WW and EE. Since in the computation of the source term of the pressure equation we have the velocities stored at the points P, WW and EE we would have a complete decoupling of the neighbouring points in the pressure equation. This allows the existence of oscillatory solutions in the discrete case which are not part of the continuous solutions.
2.4 Equations for the turbulence
The way the turbulent stresses enter into the momentum equation is well described here: https://www.openfoam.com/documentation/guides/latest/doc/guide-turbulence-ras.html.
3 References
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- ↑ Ferziger, Joel H., and Milovan Peric. Computational methods for fluid dynamics. Springer Science & Business Media, 2012.
- ↑ Jasak, Hrvoje. "Error analysis and estimation for the finite volume method with applications to fluid flows." (1996).