SimpleFoam
SimpleFoam is a steady-state solver for incompressible, turbulent flow, using the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm. In the newer releases it also includes an option to use the SIMPLEC (Semi-Implicit Method for Pressure Linked Equations Consistent) algorithm.
Contents
1 Solution Strategy
The solver follows a segregated solution strategy. This means that the equations for each variable characterizing the system (the velocity 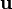 , the pressure
, the pressure 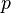 and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
 which is a function of the velocity) is resolved by computing it from the velocity and pressure values of the preceding iteration. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field
which is a function of the velocity) is resolved by computing it from the velocity and pressure values of the preceding iteration. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field  which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field
which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field  , which, if inserted in the momentum equation, delivers a divergence free velocity field
, which, if inserted in the momentum equation, delivers a divergence free velocity field 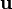 .
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
.
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
The source code can be found in simpleFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Copyright (C) 2011-2018 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application simpleFoam Description Steady-state solver for incompressible, turbulent flow, using the SIMPLE algorithm. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "singlePhaseTransportModel.H" #include "turbulentTransportModel.H" #include "simpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { #include "postProcess.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "initContinuityErrs.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (simple.loop(runTime)) { Info<< "Time = " << runTime.timeName() << nl << endl; // --- Pressure-velocity SIMPLE corrector { #include "UEqn.H" #include "pEqn.H" } laminarTransport.correct(); turbulence->correct(); runTime.write(); Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s" << " ClockTime = " << runTime.elapsedClockTime() << " s" << nl << endl; } Info<< "End\n" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Momentum Equation
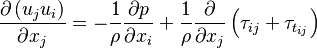 | (1) |
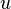 represent the velocity and
represent the velocity and
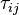 and
and 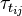 are the viscose and turbulent stresses. Not that in simpleFoam the momentum
equation solve, is divided by the constant density
are the viscose and turbulent stresses. Not that in simpleFoam the momentum
equation solve, is divided by the constant density 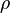 .
.
The source code can be found in UEqn.H:
// Momentum predictor
MRF.correctBoundaryVelocity(U);
tmp<fvVectorMatrix> tUEqn
(
fvm::div(phi, U)
+ MRF.DDt(U)
+ turbulence->divDevReff(U)
==
fvOptions(U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
UEqn.relax();
fvOptions.constrain(UEqn);
if (simple.momentumPredictor())
{
solve(UEqn == -fvc::grad(p));
fvOptions.correct(U);
}
In the following the numeric used to solve the momentum equation are briefly explained.
The first step performed is to assemble the matrix which is later solved to obtain the estimate of the velocity  :
:
tmp<fvVectorMatrix> tUEqn
(
fvm::div(phi, U)
+ MRF.DDt(U)
+ turbulence->divDevReff(U)
==
fvOptions(U)
);
In the usual semi discrete form it can be written as (see also [1]. ):
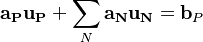 | (1) |
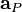 are the matrix coefficient associated with the centre point P,
are the matrix coefficient associated with the centre point P, 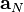 the matrix coefficients associated with all neighbours influencing the computational stencil around point P and
the matrix coefficients associated with all neighbours influencing the computational stencil around point P and 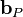 is the source therm. The sum
is the source therm. The sum 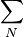 is taken over all neighbours influencing the computational stencil around point P.
is taken over all neighbours influencing the computational stencil around point P.
The next step performed is the under relax the equation:
UEqn.relax();
The under relaxation is required in order to prevent the solution to diverge. Even though the discrete equation of the momentum
equation is linear, the non linearity is resolve by using the solution of the previous iteration. This causes a large change of the new velocity leading often to divergence [2]. Using Patankar's implicit under relaxation the new semi discrete momentum equation can be written as:
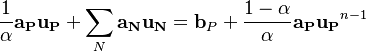 | (1) |
Here 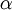 denotes the under relaxation factor and
denotes the under relaxation factor and 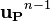 denotes the solution at the previous iteration step.
The source code for the under relaxation can be found in fvMatrix.C (see also https://www.openfoam.com/documentation/cpp-guide/html/fvMatrix_8C_source.html):
denotes the solution at the previous iteration step.
The source code for the under relaxation can be found in fvMatrix.C (see also https://www.openfoam.com/documentation/cpp-guide/html/fvMatrix_8C_source.html):
template<class Type> void Foam::fvMatrix<Type>::relax(const scalar alpha) { if (alpha <= 0) { return; } if (debug) { InfoInFunction << "Relaxing " << psi_.name() << " by " << alpha << endl; } Field<Type>& S = source(); scalarField& D = diag(); // Store the current unrelaxed diagonal for use in updating the source scalarField D0(D); // Calculate the sum-mag off-diagonal from the interior faces scalarField sumOff(D.size(), 0.0); sumMagOffDiag(sumOff); // Handle the boundary contributions to the diagonal forAll(psi_.boundaryField(), patchi) { const fvPatchField<Type>& ptf = psi_.boundaryField()[patchi]; if (ptf.size()) { const labelUList& pa = lduAddr().patchAddr(patchi); Field<Type>& iCoeffs = internalCoeffs_[patchi]; if (ptf.coupled()) { const Field<Type>& pCoeffs = boundaryCoeffs_[patchi]; // For coupled boundaries add the diagonal and // off-diagonal contributions forAll(pa, face) { D[pa[face]] += component(iCoeffs[face], 0); sumOff[pa[face]] += mag(component(pCoeffs[face], 0)); } } else { // For non-coupled boundaries add the maximum magnitude diagonal // contribution to ensure stability forAll(pa, face) { D[pa[face]] += cmptMax(cmptMag(iCoeffs[face])); } } } } if (debug) { // Calculate amount of non-dominance. label nNon = 0; scalar maxNon = 0.0; scalar sumNon = 0.0; forAll(D, celli) { scalar d = (sumOff[celli] - D[celli])/mag(D[celli]); if (d > 0) { nNon++; maxNon = max(maxNon, d); sumNon += d; } } reduce(nNon, sumOp<label>(), UPstream::msgType(), psi_.mesh().comm()); reduce ( maxNon, maxOp<scalar>(), UPstream::msgType(), psi_.mesh().comm() ); reduce ( sumNon, sumOp<scalar>(), UPstream::msgType(), psi_.mesh().comm() ); sumNon /= returnReduce ( D.size(), sumOp<label>(), UPstream::msgType(), psi_.mesh().comm() ); InfoInFunction << "Matrix dominance test for " << psi_.name() << nl << " number of non-dominant cells : " << nNon << nl << " maximum relative non-dominance : " << maxNon << nl << " average relative non-dominance : " << sumNon << nl << endl; } // Ensure the matrix is diagonally dominant... // Assumes that the central coefficient is positive and ensures it is forAll(D, celli) { D[celli] = max(mag(D[celli]), sumOff[celli]); } // ... then relax D /= alpha; // Now remove the diagonal contribution from coupled boundaries forAll(psi_.boundaryField(), patchi) { const fvPatchField<Type>& ptf = psi_.boundaryField()[patchi]; if (ptf.size()) { const labelUList& pa = lduAddr().patchAddr(patchi); Field<Type>& iCoeffs = internalCoeffs_[patchi]; if (ptf.coupled()) { forAll(pa, face) { D[pa[face]] -= component(iCoeffs[face], 0); } } else { forAll(pa, face) { D[pa[face]] -= cmptMin(iCoeffs[face]); } } } } // Finally add the relaxation contribution to the source. S += (D - D0)*psi_.primitiveField(); }
2.2 Pressure Equation
2.3 Equations for the turbulence
3 References
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):