Blasius Flat-Plate Flow Benchmark
Contents
1 Benchmarking OpenFOAM Solvers Against the Blasius Similarity Solution
Computational simulation is only as good as it accurately reflects the real world which makes benchmarking an important step in creating solvers. One option for benchmarking studies is to use analytical solutions, where available. One such solution exists that describes both velocity and temperature in a laminar boundary layer.
Two solvers will be benchmarked against the analytical solution available. The first is a modified version of icoFoam called icoHeatFoam (the steps to creating this in this tutorial: How to Add Temperature to IcoFoam). Later, the conjugateHeatFoam solver will be benchmarked as well.
First, a brief description of the Blasius flat-plate flow solution is given. The steps to creating the necessary case files and running the solution will be covered and then steps for post-processing.
Good writing skills are in great demand nowadays, so if you consider yourself to be a good writer and would like to have some extra income, try to become our freelance writer. Freelance writing jobs isn't that easy to do as it may seem from the first sight, but the fees are quite high to reward hard work.
2 Blasius Similarity Solution
The similarity solution describes the formation of a boundary layer. While solutions exist for stagnation flow, this case will look at flat-plate flow only. The full derivation of the similarity solution can be found in numerous fluid dynamics texts, such as "Viscous Fluid Flow" by Frank White, 2003. One can also see an abbreviated discussion Blasius Boundary Layer. For the time being, only the main points of the solution will be described.
The starting point of the derivation are the boundary layer equations for incompressible flow which make certain assumptions regarding the growth of a boundary layer in a high Reynolds flow:
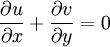
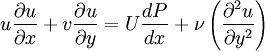
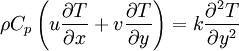
Which describe continuity, momentum transport and energy transport through the steady state boundary layer.
Because of the lack of a natural length scale in the x-direction, a similarity variable can be created given as 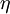 :
:
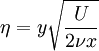
where  is the direction normal to the plate,
is the direction normal to the plate, 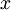 is the direction along its length with zero being the leading edge.
is the direction along its length with zero being the leading edge.
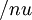 is the kinematic viscosity of the fluid and
is the kinematic viscosity of the fluid and  is the free stream velocity.
A stream function,
is the free stream velocity.
A stream function,  , can be defined by integrating the velocity from the wall boundary such that:
, can be defined by integrating the velocity from the wall boundary such that:
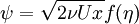
where 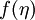 is some presently unknown function.
In the usual way, the two components of velocity are defined from this stream function:
is some presently unknown function.
In the usual way, the two components of velocity are defined from this stream function:
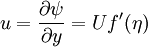
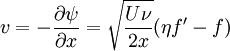
where primes ( ) denote differentiation with respect to
) denote differentiation with respect to 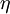 .
Applying this change of variables to the boundary-layer equations above one obtains an ordinary differential equation describing the stream function:
.
Applying this change of variables to the boundary-layer equations above one obtains an ordinary differential equation describing the stream function:
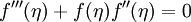
With the zero velocity condition at the wall, as well as the velocity reaching free-stream beyond the boundary layer, the following boundary conditions are supplied for this function:
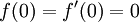
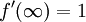
These equations can be numerically integrated and the shooting method can be used to determine the correct starting value of 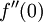 .
.
A dimensionless temperature can be defined as follows:
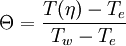 Where
Where 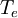 and
and 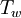 are the free-stream and wall temperatures respectively.
In similar steps as those above, a change of variables can be applied to the energy transport equation yielding an ordinary differential equation:
are the free-stream and wall temperatures respectively.
In similar steps as those above, a change of variables can be applied to the energy transport equation yielding an ordinary differential equation:
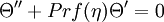
where 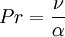 is the Prandtl number of the fluid under study.
The values of the wall temperature and free stream yield boundary conditions of 1 and 0 respectively.
Because the stream function was already solved above, integration of
is the Prandtl number of the fluid under study.
The values of the wall temperature and free stream yield boundary conditions of 1 and 0 respectively.
Because the stream function was already solved above, integration of 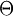 is straight-forward:
is straight-forward:
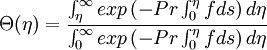
3 Mesh Construction and Physical Properties
BlockMesh will be utilized to construct the case. It is suggested that one copy the case files from the icoFoam cavity tutorial to a new case which will be modified for this test.
First, the desired mesh will have a small section of entrance flow, the flat plate will be located at x=0 to ease later comparison with the analytical theory.
The test will consist of a flat-plate held at constant temperature (275 K) and liquid water (Pr = 7) with an entrance temperature of 350 K.
We will test a free-stream velocity of 20 cm/s.
The upper boundary of the computational domain should be "far" from the flat plate.
We will take "far" to be 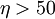 which will be made 10cm away.
which will be made 10cm away.
Begin by editing the blockMeshDict file located in the <case>/constant/polymesh subdirectory. In this tutorial, the computational domain is broken into 4 regions:
- 2 x-direction sections
- An entrance length
- The flat-plate region
- 2 y-direction sections
- A finely graded region next to the plate
- A more coarsely graded region above
Edit blockMeshDict to reflect the following information:
// * * * * * * * * * //
convertToMeters 0.001;
vertices
(
(0 0 0) //0
(35 0 0) //1
(35 10 0) //2
(0 10 0) //3
(0 0 1) //4
(35 0 1) //5
(35 10 1) //6
(0 10 1) //7
(0 100 0) //8
(35 100 0) //9
(0 100 1) //10
(35 100 1) //11
(-20 0 0) //12
(-20 0 1) //13
(-20 10 0) //14
(-20 10 1) //15
(-20 100 0) //16
(-20 100 1) //17
);
blocks
(
hex (0 1 2 3 4 5 6 7) (35 30 1) simpleGrading (6 10 1)
hex (3 2 9 8 7 6 11 10) (35 15 1) simpleGrading (6 3 1)
hex (12 0 3 14 13 4 7 15) (20 30 1) simpleGrading (.1 10 1)
hex (14 3 8 16 15 7 10 17) (20 15 1) simpleGrading (.1 3 1)
);
edges
(
);
patches
(
wall top
(
(8 9 11 10)
(16 8 10 17)
)
wall inlet
(
(14 16 17 15)
(12 14 15 13)
)
wall outlet
(
(9 2 6 11)
(2 1 5 6)
)
wall plate
(
(0 4 5 1)
)
wall symmBound
(
(12 13 4 0)
)
empty frontAndBack
(
(3 0 1 2)
(7 6 5 4)
(8 3 2 9)
(10 11 6 7)
(14 12 0 3)
(15 7 4 13)
(16 14 3 8)
(17 10 7 15)
)
);
mergePatchPairs
(
);
// ************************************************************************* //
Aside: an important note regarding the use of the blockMesh utility is the order of defining blocks and patches. Blocks are defined such that the order of vertices create a local coordinate system. The number of cells and cell grading is determined according to this local coordinate system, which may not be the same for all blocks if the same ordering pattern is not used for all. In the case of patches, each must be defined such that the face normal (using the right-hand rule) points away, or out of, the computational domain. Failure to adhere to the guidelines for vertex ordering detailed in the user manual can result in negative volumes which will not appear until a solver attempts to use the mesh.
The transport properties of liquid water are:
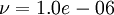
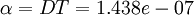
These items should be entered into the transportProperties file.
4 Boundary and Initial Conditions
The patches described above can be set to either wall or patch type in the boundary file because the laminar solvers do not distinguish between these patch types.
Appropriate boundary conditions for velocity are to set the entrance bottom plane and outlet as zeroGradient patches. The inlet and top patches are "fixedValue" patches with velocity of (0.2 0 0). The plate patch is "fixedValue" with a velocity of (0 0 0). Time can be saved by setting the internalField to a uniform (0.2 0 0).
For the pressure boundary conditions, the outlet is a fixedValue type with value 0. All other boundary patches are zeroGradient.
Temperature boundary conditions mimic the velocity field. The inlet and top patches are "fixedValue" with a value of 350. The symmBound and outlet patches receive a zeroGradient boundary. Finally, the plate itself is a fixedValue boundary of 275.
The following shows the information in the /0/T file:
dimensions [0 0 0 1 0 0 0];
internalField uniform 350;
boundaryField
{
top
{
type fixedValue;
value uniform 350;
}
inlet
{
type fixedValue;
value uniform 350;
}
outlet
{
type zeroGradient;
}
plate
{
type fixedValue;
value uniform 275;
}
symmBound
{
type zeroGradient;
}
frontAndBack
{
type empty;
}
}
5 Running the Case and post-processing
The last step before running the case is providing the correct settings to the control dictionary. Edit the controlDict file such that the case will run to 1 second, which should be enough time to reach steady state. Estimating time to run is complicated by having both velocity and temperature solutions evolving at the same time. The temperature equilibrates much slower than the velocity does (1/Pr as fast) and depends on the velocity solution.
A time step of 0.001 provides a maximum Courant number of approximately 0.75. An example controlDict file is shown here:
application icoHeatFoam; startFrom startTime; startTime 0; stopAt endTime; endTime 1; deltaT 0.001; writeControl timeStep; writeInterval 15; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression uncompressed; timeFormat general; timePrecision 6; runTimeModifiable yes;
One can run the case and examine the solution.
Case files are included in the following tarball: Media:icoHeatFoam-flatPlate2.tar.gz
The sample utility will be used to pull more quantitative data from the solution.
It is suggested that you copy an existing sampleDict file from another tutorial, such as the stressed plate tutorial in the user manual.
Several lines will be created to read the velocity and temperature of the fluid. These will be defined such that the starting point is 1cm above the plate and ends at y=0.0. This method is chosen to avoid a small bug in the sample utility which sometimes causes it to hang if the starting point is defined too close to the boundary of the domain.
The two items read will be the x component of the velocity and the temperature. Rather than us the Ucomponents utility as in the user manual tutorial, the velocity component we desire will be obtained by specifying U.component(0). The one drawback of this method is that the utility will create filenames with the special characters "(" and ")" in them.
The sampleDict file should resemble the following:
interpolationScheme cellPoint;
writeFormat raw;
sampleSets
(
uniform
{
name x005;
axis y;
start (0.005 0.01 0.0005);
end (0.005 0.0 0.0005);
nPoints 100;
}
uniform
{
name x015;
axis y;
start (0.015 0.01 0.0005);
end (0.015 0.0 0.0005);
nPoints 100;
}
uniform
{
name x025;
axis y;
start (0.025 0.01 0.0005);
end (0.025 0.0 0.0005);
nPoints 100;
}
uniform
{
name x030;
axis y;
start (0.03 0.01 0.0005);
end (0.03 0.0 0.0005);
nPoints 100;
}
);
fields
(
U.component(0)
T
);
Run the sample utility which, as written, will proceed through every available time step available. Each subset in the sample utility produces its own file showing the <name> value at the start.
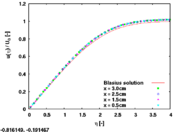
A closer examination of the data can be made from the last time step can be made. By renaming the data files to avoid the special characters, a gnuplot plotting script can be written which will compare the obtained data to the Blasius solution itself. This could look like the following:
reset
set term x11 enhanced font 'Helvetica, 18'
U0 = 0.2
eta(r, s) = r * sqrt(U0 / (2 * 1e-6 * s))
set key inside bottom right vertical Left
set pointsize 1.5
set xr [0:4]
set yr [0:0.025]
set xlabel '{/Symbol h} [-]'
set ylabel 'U_x / U_0 [m/s]'
plot 'BlasiusF.dat' u ($1):( $3) t 'Blasius solution' w l,\
'x030_Ux_T.xy' every 2 u ( eta($1, 0.03) ):($2/U0) \
t 'x = 3.0cm' w points pt 5,\
'x025_Ux_T.xy' every 2 u ( eta($1, 0.025) ):($2/U0) \
t 'x = 2.5cm' w points pt 6,\
'x015_Ux_T.xy' every 2 u ( eta($1, 0.015) ):($2/U0) \
t 'x = 1.5cm' w points pt 9,\
'x005_Ux_T.xy' every 2 u ( eta($1, 0.005) ):($2/U0) \
t 'x = 0.5cm' w points pt 11
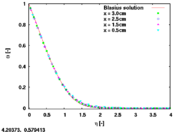
This and a similar script for comparing the 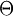 variable produce the following graphs:
variable produce the following graphs:
All necessary files to produce these graphs are included in this tarball: Media:gnuplot_blasius_compare.tar.gz
6 Discussion of the results
The first main point is that this is not an optimal setup for comparison because of the closed boundary at the top of the solution domain. The growth of the boundary layer necessarily accelerates the fluid elsewhere to maintain fluid continuity. As a result, the "apparent" free-stream velocity is slightly higher than the 0.2m/s which was specified in the case files. Even with this acceleration the OpenFOAM solution is in good agreement with the analytical solution as indicated in the two graphs comparing the data against the analytical solution. In particular, the temperature solution shows excellent agreement with the analytical solution.