BuoyantBoussinesqPisoFoam
Contents
1 Equations
In this section, the equations used by buoyantBoussinesqPisoFoam solver are presented or derived from other equations. In RANS or LES mode (in its current form, it is RANS only, but can be modified to be more general following pisoFoam as shown in Section 4), it also solves turbulence equations which are not relevant to this discussion and not shown here. Although the continuity equation is presented, buoyantBoussinesqPisoFoam does not actually solve it; instead, it solves a pressure Poisson equation that enforces continuity as discussed in Section 2 that describes the PISO algorithm. Unlike in compressible flows, this solver is meant for incompressible flow (and its relative buoyantPisoFoam is meant for lightly compressible flows) so the coupling between density and pressure becomes very stiff. More conventional schemes that actually solve the continuity equation and no pressure equation no longer work well (or at all) since the dominant variable between pressure and density is pressure. For that reason, an equation for pressure is solved.
1.1 Continuity Equation
The constant-density filtered (LES) or averaged (RANS) continuity equation is
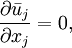 | (1) |
where bar denotes a resolved or mean quantity.
1.2 Momentum Equation
The constant-density (except in the gravity term) filtered or averaged momentum equation is
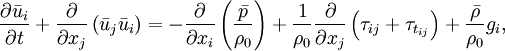 | (2) |
where 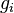 is the gravity acceleration vector,
is the gravity acceleration vector, 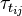 is the turbulent stress tensor, and
is the turbulent stress tensor, and 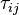 is the resolved or mean stress tensor due to molecular viscosity and is given by
is the resolved or mean stress tensor due to molecular viscosity and is given by
![\tau_{ij} = \mu \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right)-\frac{2}{3}\left( \frac{\partial \bar{u}_k}{\partial x_k} \right)\delta_{ij} \right],](/images/math/4/3/8/438308180df23d46d6e1e379abb32197.png) | (3) |
where  is the molecular viscosity. Rewriting Equation 2 using Equation 3 with constant viscosity,
is the molecular viscosity. Rewriting Equation 2 using Equation 3 with constant viscosity, 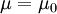 , and rearranging the gravity term yields
, and rearranging the gravity term yields
![\frac{\partial \bar{u}_i}{\partial t} + \frac{\partial}{\partial x_j} \left( \bar{u}_j \bar{u}_i \right) =
-\frac{\partial}{\partial{x_i}}\left( \frac{\bar{p}}{\rho_0} \right) + \frac{\partial}{\partial x_j} \left\{ \nu_0 \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) - \frac{2}{3} \left( \frac{\partial \bar{u}_k}{\partial x_k}\right) \delta_{ij} \right] - R_{ij} \right\} + g_i\left( 1 + \frac{\bar{\rho}-\rho_0}{\rho_0} \right),](/images/math/d/0/1/d018f6451a05a29c3bdaec692da38039.png) | (4) |
where 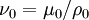 is the kinematic viscosity and
is the kinematic viscosity and 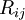 is either the RANS Reynolds stress tensor or the LES sub-grid-scale Reynolds stress tensor depending upon which method is used. The Reynolds stress tensor can be further split into a deviatoric and an isotropic part
is either the RANS Reynolds stress tensor or the LES sub-grid-scale Reynolds stress tensor depending upon which method is used. The Reynolds stress tensor can be further split into a deviatoric and an isotropic part
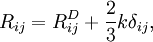 | (5) |
where 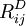 is the deviatoric part and
is the deviatoric part and 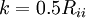 is the RANS turbulent kinetic energy or the LES sub-grid-scale kinetic energy. Equation 4 can be further rearranged as follows:
is the RANS turbulent kinetic energy or the LES sub-grid-scale kinetic energy. Equation 4 can be further rearranged as follows:
![\frac{\partial \bar{u}_i}{\partial t} + \frac{\partial}{\partial x_j} \left( \bar{u}_j \bar{u}_i \right) =
-\frac{\partial}{\partial{x_i}}\left( \frac{\bar{p}}{\rho_0} + \frac{2}{3}k \right) + \frac{\partial}{\partial x_j} \left\{ \nu_0 \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) - \frac{2}{3} \left( \frac{\partial \bar{u}_k}{\partial x_k} \right) \delta_{ij} \right] - R_{ij}^D \right\} + g_i\left( 1 + \frac{\bar{\rho}-\rho_0}{\rho_0} \right).](/images/math/7/a/a/7aa2fe5157a17c596cfb96f9ccf0121e.png) | (6) |
The quantity inside the derivative of the first term on the right-hand side of Equation 6 can be denoted 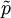 , which is a modified mean or resolved kinematic pressure[1].
, which is a modified mean or resolved kinematic pressure[1]. buoyantBoussinesqPisoFoam appears to use modified pressure like this, but it unclear what pressure is being written out in the solution file (see CFD Online discussion here). The quantity inside the parentheses of the last term on the right-hand side is the effective kinematic density, 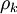 . Using the Boussinesq approximation for stratified flow, the effective kinematic density can be expressed as
. Using the Boussinesq approximation for stratified flow, the effective kinematic density can be expressed as
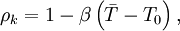 | (7) |
where 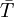 is the resolve or mean temperature in Kelvin,
is the resolve or mean temperature in Kelvin, 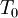 is a reference temperature in Kelvin, and
is a reference temperature in Kelvin, and 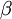 is the coefficient of expansion with temperature of the fluid in Kelvin
is the coefficient of expansion with temperature of the fluid in Kelvin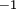 . According to Ferziger and Peric[2], the Boussinesq approximation introduces errors less than 1% for temperature variations of 2K for water or 15K for air. If a linear turbulent viscosity or sub-grid-scale viscosity hypothesis is used, as is often the case (unless a full Reynolds stress or non-linear model is used), then
. According to Ferziger and Peric[2], the Boussinesq approximation introduces errors less than 1% for temperature variations of 2K for water or 15K for air. If a linear turbulent viscosity or sub-grid-scale viscosity hypothesis is used, as is often the case (unless a full Reynolds stress or non-linear model is used), then
![R_{ij}^D = -\nu_t \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) - \frac{2}{3} \left( \frac{\partial \bar{u}_k}{\partial u_k} \right) \delta_{ij} \right],](/images/math/c/5/d/c5d9ad7471aa74363acee3a60d6e158e.png) | (8) |
where 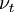 is the turbulent or sub-grid-scale turbulent viscosity. Substituting Equations 7 and 8 into Equation 6 yields
is the turbulent or sub-grid-scale turbulent viscosity. Substituting Equations 7 and 8 into Equation 6 yields
![\frac{\partial \bar{u}_i}{\partial t} + \frac{\partial}{\partial x_j} \left( \bar{u}_j \bar{u}_i \right) - \frac{\partial}{\partial x_j} \left\{ \nu_{eff} \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) - \frac{2}{3} \left( \frac{\partial \bar{u}_k}{\partial x_k} \right) \delta_{ij} \right] \right\}=
-\frac{\partial \tilde{p}}{\partial{x_i}} + g_i\left[ 1-\beta\left( \bar{T} - T_0 \right) \right],](/images/math/9/a/b/9abea1ec18b71c4cbcf0b3513a3068af.png) | (9) |
where 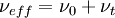 is the effective kinematic viscosity. Please note that Equation 9 is only valid if the linear turbulent or sub-grid-scale viscosity hypothesis is used, which is most often the case. Also, this equation contains a 2/3 multiplied by the divergence of velocity term, which according to the continuity equation (Equation 1), is zero. This term will be left in the momentum equation for reasons to be discussed later.
is the effective kinematic viscosity. Please note that Equation 9 is only valid if the linear turbulent or sub-grid-scale viscosity hypothesis is used, which is most often the case. Also, this equation contains a 2/3 multiplied by the divergence of velocity term, which according to the continuity equation (Equation 1), is zero. This term will be left in the momentum equation for reasons to be discussed later.
1.3 Temperature Equation
The instantaneous internal energy equation is
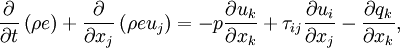 | (10) |
where  is internal energy and
is internal energy and 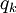 is the conductive heat flux leaving the control volume in the integral form of Equation 10[3]. The first term on the right-hand side of Equation 10 contains the divergence of velocity which the continuity equation dictates to be zero. Also, according to Ferziger and Peric[4] and White[5], the second term on the right-hand side of Equation 10 can be removed for incompressible flows. This is true because incompressible flows are of low Mach number, and therefore low speed. This term is of the order
is the conductive heat flux leaving the control volume in the integral form of Equation 10[3]. The first term on the right-hand side of Equation 10 contains the divergence of velocity which the continuity equation dictates to be zero. Also, according to Ferziger and Peric[4] and White[5], the second term on the right-hand side of Equation 10 can be removed for incompressible flows. This is true because incompressible flows are of low Mach number, and therefore low speed. This term is of the order 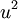 , which is small for low velocity and has a smaller effect on internal energy than heat conduction. With these simplifications, the internal energy equation becomes
, which is small for low velocity and has a smaller effect on internal energy than heat conduction. With these simplifications, the internal energy equation becomes
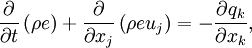 | (11) |
Next, Equation 11 is filtered or averaged, and, during this procedure, the quantity inside the convection term is decomposed into ![\rho \left[ (\bar{e} + e')(\bar{u}_j + u'_j) \right]](/images/math/9/3/b/93b821a81353b2df9d7d64b16744d84a.png) where the prime denotes a residual or fluctuating quantity. This yields a resolved or mean internal energy equation as follows:
where the prime denotes a residual or fluctuating quantity. This yields a resolved or mean internal energy equation as follows:
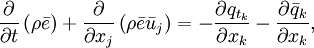 | (12) |
where 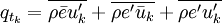 is the turbulent heat flux.
is the turbulent heat flux.
Fourier's law of heat conduction states that
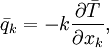 | (13) |
where 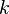 is the fluid conductivity. Using this idea, an analogy may be made for the turbulent heat flux such that
is the fluid conductivity. Using this idea, an analogy may be made for the turbulent heat flux such that
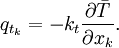 | (14) |
Approximating this a constant density and constant viscosity flow in which 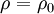 and
and 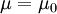 , using Equations 13 and 14, using the fact that
, using Equations 13 and 14, using the fact that 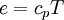 , and manipulating of the coefficient of the heat fluxes makes Equation 12 become
, and manipulating of the coefficient of the heat fluxes makes Equation 12 become
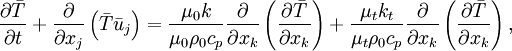 | (15) |
where 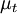 is turbulent viscosity. Rearranging the right-hand side, and recognizing that
is turbulent viscosity. Rearranging the right-hand side, and recognizing that 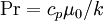 and
and 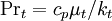 , Equation 15 becomes
, Equation 15 becomes
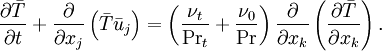 | (16) |
Finally, by combining the heat transfer coefficient as
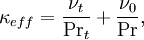 | (17) |
the resolved or mean temperature equation is
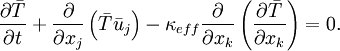 | (18) |
2 PISO Algorithm
More information about Issa's PISO (Pressure-Implicit with Splitting of Operators) algorithm is given in References [6],[7],[8],[9],[10]. Rather than solve all of the coupled equations in a coupled or iterative sequential fashion, PISO splits the operators into an implicit predictor and multiple explicit corrector steps. This scheme is not thought of as iterative, and very few corrector steps are necessary to obtain desired accuracy. At each time step with buoyantBoussinesqPisoFoam, velocity and temperature are predicted, and then pressure and velocity are corrected. Temperature is not corrected for an unknown reason; however, Oliveira and Issa recommend temperature correction for incompressible flow using the Boussinesq approximation[11]. It is possible that since this is not really compressible flow because the Boussinesq approximation is used, the maximum difference in temperature in a problem suitable for this solver is small and a corrector is not necessary.
The PISO algorithm can be understood, for simplicity, by considering a one-dimensional, inviscid flow along the 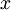 -direction in which gravity acts in that direction as well. Here
-direction in which gravity acts in that direction as well. Here 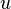 could be replaced by
could be replaced by 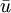 in RANS or LES with no consequence to understanding the PISO algorithm. The momentum equation simplifies to
in RANS or LES with no consequence to understanding the PISO algorithm. The momentum equation simplifies to
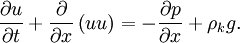 | (19) |
2.1 Predictor
As an example, if Euler implicit time stepping is used with linear interpolation of values to the cell faces and linearization of the convective term by taking the convective velocity to be from the old time step  (this treatment of the convective term is the same in as OpenFOAM according to Nilsson, then the discretized implicit velocity predictor form of Equation 19 is
(this treatment of the convective term is the same in as OpenFOAM according to Nilsson, then the discretized implicit velocity predictor form of Equation 19 is
![\left[ \frac{1}{\Delta t}+\left( \frac{u_{i+\frac{1}{2}}^n-u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) \right] \Delta V u_i^{*} + \left( \frac{u_{i+\frac{1}{2}}^n}{2 \Delta x} \right) \Delta V u_{i+1}^{*} - \left( \frac{u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) \Delta V u_{i-1}^{*} = \frac{u_i^n}{\Delta t} \Delta V - \left. \left( \frac{\partial p}{\partial x} \right) \right|_i^n \Delta V + \left. \left( \rho_k g \right) \right|_i^n \Delta V,](/images/math/b/7/e/b7e8dc203126498772a4be0d65f3b26d.png) | (20) |
where the predicted values are denoted by 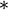 . Notice that pressure is taken from the old time level
. Notice that pressure is taken from the old time level  since it is yet unknown, which makes the predicted velocity non-divergence free. Equation 20 is what is actually solved in
since it is yet unknown, which makes the predicted velocity non-divergence free. Equation 20 is what is actually solved in UEqn.H as described in Section 3.1. However, the cell volumes 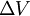 must be divided out as follows to get the correct coefficient matrices and vectors that are used in the corrector step
must be divided out as follows to get the correct coefficient matrices and vectors that are used in the corrector step
![\left[ \frac{1}{\Delta t}+\left( \frac{u_{i+\frac{1}{2}}^n-u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) \right] u_i^{*} + \left( \frac{u_{i+\frac{1}{2}}^n}{2 \Delta x} \right) u_{i+1}^{*} -
\left( \frac{u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) u_{i-1}^{*} = \frac{u_i^n}{\Delta t} - \left. \left( \frac{\partial p}{\partial x} \right) \right|_i^n + \left. \left( \rho_k g \right) \right|_i^n.](/images/math/6/e/a/6eace33f826263df08fa12ae27345a17.png) | (21) |
In solution vector form, this becomes (where vector refers to the vector of the solution to 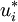 at all points
at all points 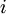 ) as
) as
 | (22) |
where 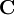 is the coefficient array multiplying the solution
is the coefficient array multiplying the solution 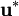 vector and
vector and 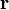 are the right-hand side explicit source terms excluding the pressure gradient. One can see that the inclusion of the viscous and turbulent stress terms would modify the coefficient matrix
are the right-hand side explicit source terms excluding the pressure gradient. One can see that the inclusion of the viscous and turbulent stress terms would modify the coefficient matrix 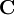 and not change the general form of the matrix-vector equation. This equation can be changed to
and not change the general form of the matrix-vector equation. This equation can be changed to
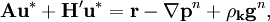 | (23) |
where 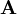 is the diagonal matrix of
is the diagonal matrix of 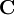 and
and 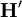 is the off-diagonal matrix as
is the off-diagonal matrix as 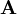 (in other words,
(in other words, 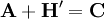 ). Using a matrix solver, Equation 23 can be readily solved for the predicted velocity
). Using a matrix solver, Equation 23 can be readily solved for the predicted velocity 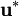 . Equation 23 is a generalization of what is solved during the velocity predictor step of
. Equation 23 is a generalization of what is solved during the velocity predictor step of buoyantBoussinessqPisoFoam as discussed in Section 3.1.
2.2 Corrector
Next, the discretized explicit velocity corrector is written as
![\left[ \frac{1}{\Delta t}+\left( \frac{u_{i+\frac{1}{2}}^n-u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) \right] u_i^{**} + \left( \frac{u_{i+\frac{1}{2}}^n}{2 \Delta x} \right) u_{i+1}^{*} -
\left( \frac{u_{i-\frac{1}{2}}^n}{2 \Delta x} \right) u_{i-1}^{*} = \frac{u_i^n}{\Delta t} - \left. \left( \frac{\partial p}{\partial x} \right) \right|_i^* + \left. \left( \rho_k g \right) \right|_i^n.](/images/math/c/c/5/cc5a25499bc43183fadcddcfdb0bf008.png) | (24) |
Here, the first corrected velocity 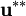 is being solved from the predicted velocity
is being solved from the predicted velocity 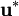 , old velocity
, old velocity  , and the first corrected pressure
, and the first corrected pressure 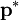 . The problem is that the corrected pressure is yet unknown --- all that is known is the old pressure. Like in Equation 23, Equation 24 can be expressed in matrix-vector form as
. The problem is that the corrected pressure is yet unknown --- all that is known is the old pressure. Like in Equation 23, Equation 24 can be expressed in matrix-vector form as
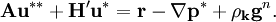 | (25) |
Introducing 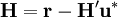 and inverting
and inverting 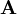 (which is easy since it is diagonal), Equation 25 becomes
(which is easy since it is diagonal), Equation 25 becomes
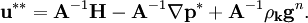 | (26) |
The point of the corrector step is to make the corrected velocity field divergence free so that it adheres to the continuity equation. Therefore, taking the divergence of Equation 26 and recognizing that 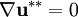 due to continuity (Equation 1) yields a Poisson equation for the first corrected pressure
due to continuity (Equation 1) yields a Poisson equation for the first corrected pressure
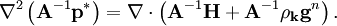 | (27) |
With the first corrected pressure 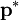 , Equation 26 can be solved for the first corrected velocity
, Equation 26 can be solved for the first corrected velocity 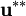 .
.
Further correction steps can be applied using the same 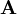 matrix and
matrix and 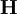 vector (this is convenient computationally since they can be stored in the computer's memory once and recalled as necessary). For example the second correction step would consist of the equations.
vector (this is convenient computationally since they can be stored in the computer's memory once and recalled as necessary). For example the second correction step would consist of the equations.
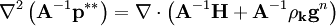 | (28) |
and
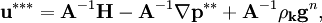 | (29) |
where 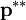 and
and 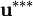 are the second corrected pressure and velocity, respectively. Equations 26 and 27 are a generalization of what is solved during the corrector step in
are the second corrected pressure and velocity, respectively. Equations 26 and 27 are a generalization of what is solved during the corrector step in buoyantBoussinessqPisoFoam as discussed in Section 3.3.
In this example, first-order Euler implicit time stepping with second-order linear interpolation has been used. This method is equally applicable with other forms of implicit time stepping, such as Crank-Nicholson or second-order backward, and interpolation schemes. The same general results will follow but with modifications to the 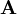 matrix and
matrix and 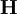 vector. Issa[12] states that if a second-order accurate time stepping scheme is used, then three corrector steps should be used to reduce the discretization error due to the PISO algorithm to second-order. For flow in which a temperature equation (or other equations) are necessary, Oliveira and Issa[13] also includes a corrector for those equations in the corrector loop.
vector. Issa[12] states that if a second-order accurate time stepping scheme is used, then three corrector steps should be used to reduce the discretization error due to the PISO algorithm to second-order. For flow in which a temperature equation (or other equations) are necessary, Oliveira and Issa[13] also includes a corrector for those equations in the corrector loop. buoyantBoussinesqPisoFoam does not do this --- temperature is simply predicted from the last time level and never corrected. Therefore, it may need to be modified to provide temperature correction.
3 Implementation in OpenFOAM
The code for buoyantBoussinesqPisoFoam is in applications\solvers\heatTransfer\buoyantBoussinesqPisoFoam\ and the driver code is buoyantBoussinesqPisoFoam.C. In that code, one can seen that buoyantBoussinesqPisoFoam first predicts velocity by solving the velocity equation using the code in UEqn.H. It then predicts temperature by solving the temperature equation using the code in TEqn.H. After this, the corrector loop (denoted the "PISO loop" in the code) is entered and pressure and velocity correctors are executed using the code in pEqn.H over some specified number of correction steps.
3.1 Velocity Predictor
The velocity is predicted implicitly in UEqn.H because of the greater stability of implicit methods, which means that a set of coupled linear equations, expressed in matrix-vector form as 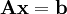 , are solved. Therefore, the implicit left-hand side of the equation is first set up using the following code:
, are solved. Therefore, the implicit left-hand side of the equation is first set up using the following code:
00003 fvVectorMatrix UEqn 00004 ( 00005 fvm::ddt(U) 00006 + fvm::div(phi, U) 00007 + turbulence->divDevReff(U) 00008 );
The fvm class stands for "finite-volume matrix", and is used when operations are to be implicit and a left-hand side matrix is formed[14]. This is opposed to the fvc class, which stands for "finite-volume calculus", and is for explicit operations, such as forming the right-hand side of the matrix equation[15]. The fvm::ddt(U) term is the first time derivative of velocity. The + fvm::div(phi, U) is the divergence of the velocity flux, phi, multiplied by velocity, or, in other words, the convection of velocity. The meaning of the + turbulence->divDevReff(U) term requires examination of the code for RANS or LES models.
3.1.1 The Meaning of divDevReff(U)
First, examining the incompressible 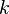 -
-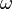 implementation at
implementation at src\turbulenceModels\incompressible\RAS\kOmega\kOmega.C, one can see that divDevReff(U) is defined as the following:
00190 tmp<fvVectorMatrix> kOmega::divDevReff(volVectorField& U) const 00191 { 00192 return 00193 ( 00194 - fvm::laplacian(nuEff(), U) 00195 - fvc::div(nuEff()*dev(fvc::grad(U)().T())) 00196 ); 00197 }
For the LES models, the coding is the same except that the term is referred to as divDevBeff(U), but it is later copied over to divDevReff(U) in src\turbulenceModels\(in)compressible\LES\LESModel\LESModel.H. In vector notation, this coding for divDevReff(U) translates to
![\mathrm{divDevReff}\left( \bar{\mathbf{u}} \right) = -\nabla^2 \left( \nu_{eff} \; \bar{\mathbf{u}} \right) - \nabla \cdot \left\{ \nu_{eff} \; \textrm{dev} \left[ \left( \nabla \bar{\mathbf{u}} \right)^T \right] \right\},](/images/math/0/e/0/0e059ef645856172e3421b77712de987.png) | (30) |
where the dev operator is defined in src\OpenFOAM\primitives\Tensor\TensorI.H as the deviatoric part of the tensor as follows:
00439 //- Return the deviatoric part of a tensor 00440 template <class Cmpt> 00441 inline Tensor<Cmpt> dev(const Tensor<Cmpt>& t) 00442 { 00443 return t - SphericalTensor<Cmpt>::oneThirdI*tr(t); 00444 }
This appears to translate to 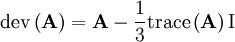 , where
, where 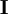 is the identity matrix. Please note that in the same file, the
is the identity matrix. Please note that in the same file, the dev2 operator is defined as follows:
00447 //- Return the deviatoric part of a tensor 00448 template <class Cmpt> 00449 inline Tensor<Cmpt> dev2(const Tensor<Cmpt>& t) 00450 { 00451 return t - SphericalTensor<Cmpt>::twoThirdsI*tr(t); 00452 }
This appears to translate to 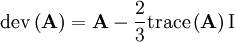 . With this information, Equation 30 becomes
. With this information, Equation 30 becomes
![\mathrm{divDevReff}\left( \bar{\mathbf{u}} \right) = -\nabla^2 \left( \nu_{eff} \; \bar{\mathbf{u}} \right) - \nabla \cdot \left\{ \nu_{eff} \left[ \left( \nabla \bar{\mathbf{u}} \right)^T - \frac{1}{3}\mathrm{trace}\left[ \left( \nabla \bar{\mathbf{u}} \right)^T \right] \mathbf{I} \right] \right\},](/images/math/d/7/f/d7f02e6a3cbe554916f0251a080d61e3.png) | (31) |
which in tensor notation is
![\mathrm{divDevReff}\left( \bar{u}_i \right) = -\frac{\partial}{\partial x_j}\frac{\partial}{\partial x_j} \left( \nu_{eff} \; \bar{u}_i \right)
-\frac{\partial}{\partial x_j} \left\{ \nu_{eff} \left[ \frac{\partial \bar{u}_j}{\partial x_i} - \frac{1}{3} \left( \frac{\partial \bar{u}_k}{\partial x_k} \right) \delta_{ij} \right] \right\},](/images/math/d/5/c/d5cdd61be7069c3e96d4445268bd2576.png) | (32) |
and rearranges to
![\mathrm{divDevReff}\left( \bar{u}_i \right) = -\frac{\partial}{\partial x_j} \left\{ \nu_{eff} \left[ \left( \frac{\partial \bar{u}_i}{\partial x_j} + \frac{\partial \bar{u}_j}{\partial x_i} \right) - \frac{1}{3} \left( \frac{\partial \bar{u}_k}{\partial x_k} \right) \delta_{ij} \right] \right\}.](/images/math/a/2/f/a2f61a24a2b2d59aa36cc97beae3a8db.png) | (33) |
This stress term differs from the stress term in Equation 9 in the subtraction of 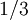 the divergence of velocity rather than
the divergence of velocity rather than  . The other incompressible RANS and LES models also include this discrepancy. The compressible RANS and LES models, though, include the correct 2/3 fraction through the use of the
. The other incompressible RANS and LES models also include this discrepancy. The compressible RANS and LES models, though, include the correct 2/3 fraction through the use of the dev2 operator as shown in the following code from compressible SST model located in the directory src\turbulenceModels\compressible\RAS\kOmegaSST\kOmegaSST.C:
00314 tmp<fvVectorMatrix> kOmegaSST::divDevRhoReff(volVectorField& U) const 00315 { 00316 return 00317 ( 00318 - fvm::laplacian(muEff(), U) - fvc::div(muEff()*dev2(fvc::grad(U)().T())) 00319 ); 00320 }
Therefore, it seems that this is a coding error in the incompressible models. In the incompressible case, the divergence of velocity should be zero according to Equation 1, but it seem correct to keep the divergence term in the incompressible momentum equations. During the velocity predictor step, the velocity field at the last time step may not be divergence free due to initial conditions or insufficient pressure correction. Furthermore, during the velocity corrector step, the velocity field is not divergence free (that is why it is being corrected), so the divergence term should be retained. Discussion about this is on the CFD Online forum here.
We now continue in understanding the velocity predictor step in UEqn.H. Next, the right-hand side of the equation set is formed in the following code:
00012 if (momentumPredictor) 00013 { 00014 solve 00015 ( 00016 UEqn 00017 == 00018 fvc::reconstruct 00019 ( 00020 ( 00021 fvc::interpolate(rhok)*(g & mesh.Sf()) 00022 - fvc::snGrad(p)*mesh.magSf() 00023 ) 00024 ) 00025 ); 00026 }
It can be seen that the implicit left hand side, described above, and stored in the array UEqn multiplied by the solution vector is set equal to two terms. The first term interpolates 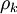 to the cell faces and multiplies it by
to the cell faces and multiplies it by 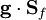 over all of the faces, where
over all of the faces, where 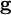 is the gravity acceleration vector and
is the gravity acceleration vector and 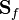 is the cell face area vector which points normal to the face (notice that the
is the cell face area vector which points normal to the face (notice that the & symbol denotes the inner product as defined in TensorI.H). The second term is the negative surface normal gradient of 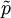 multiplied by surface area over all of the cell faces. The
multiplied by surface area over all of the cell faces. The reconstruct command reconstructs a volume field from a face flux field. The volume field is reconstructed from face values rather than simply using the cell center values from the beginning (as is done with the pressure term in the non-buoyant solver pisoFoam) in order to create a pseudo-staggered grid setup on OpenFOAM's standard co-located grid as discussed on the CFD Online forum here. This method is effectively a representation of Rhie-Chow interpolation, which aims to remove checker-board pressure oscillations that may occur on co-located grids (due to pressure at a cell only depending on adjacent cells and not the cell in question also). The resulting set of linear equations is then solved with a matrix solver to yield the predicted velocity.
3.2 Temperature Predictor
As in the velocity predictor, the temperature is predicted implicitly in TEqn.H. The implicit left-hand side is assembled in lines 2--13 the following code:
00001 { 00002 volScalarField kappaEff 00003 ( 00004 "kappaEff", 00005 turbulence->nu()/Pr + turbulence->nut()/Prt 00006 ); 00007 00008 fvScalarMatrix TEqn 00009 ( 00010 fvm::ddt(T) 00011 + fvm::div(phi, T) 00012 - fvm::laplacian(kappaEff, T) 00013 ); 00014 00015 TEqn.relax(); 00016 00017 TEqn.solve(); 00018 00019 rhok = 1.0 - beta*(T - TRef); 00020 }
First, 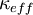 is computed using the same formulation as given in Equation 17. Then, the left hand side terms are the first time derivative of T (
is computed using the same formulation as given in Equation 17. Then, the left hand side terms are the first time derivative of T (fvm::ddt(T)) plus the convection of T (fvm::div(phi, T)) minus the Laplacian of 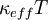 (
(fvm::laplacian(kappaEff, T)). This formulation matches the temperature equation (Equation 18). This is a linear set of equations that is then solved by TEqn.solve();. Finally, at line 19, 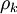 is updated based on the new value of temperature using
is updated based on the new value of temperature using rhok = 1.0 - beta*(T - TRef), which agrees with the Boussinesq approximation given in Equation 7.
3.3 Corrector Loop
The corrector steps take place in the file pEqn.H which is as follows:
00001 { 00002 volScalarField rUA("rUA", 1.0/UEqn.A()); 00003 surfaceScalarField rUAf("(1|A(U))", fvc::interpolate(rUA)); 00004 00005 U = rUA*UEqn.H(); 00006 00007 surfaceScalarField phiU 00008 ( 00009 (fvc::interpolate(U) & mesh.Sf()) 00010 + fvc::ddtPhiCorr(rUA, U, phi) 00011 ); 00012 00013 phi = phiU + rUAf*fvc::interpolate(rhok)*(g & mesh.Sf()); 00014 00015 for (int nonOrth=0; nonOrth<=nNonOrthCorr; nonOrth++) 00016 { 00017 fvScalarMatrix pEqn 00018 ( 00019 fvm::laplacian(rUAf, p) == fvc::div(phi) 00020 ); 00021 00022 if (corr == nCorr-1 && nonOrth == nNonOrthCorr) 00023 { 00024 pEqn.solve(mesh.solver(p.name() + "Final")); 00025 } 00026 else 00027 { 00028 pEqn.solve(mesh.solver(p.name())); 00029 } 00030 00031 if (nonOrth == nNonOrthCorr) 00032 { 00033 phi -= pEqn.flux(); 00034 } 00035 } 00036 00037 U += rUA*fvc::reconstruct((phi - phiU)/rUAf); 00038 U.correctBoundaryConditions(); 00039 00040 #include "continuityErrs.H" 00041 }
pEqn.H is called from within the corrector "PISO" loop inside the driver code so that as many corrections as specified in fvSolutions can be made.
Before actually making the corrections, some variables must be setup in the first part of this code. The 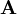 matrix is inverted as it is in Equations 26 and 27 and stored as the variable
matrix is inverted as it is in Equations 26 and 27 and stored as the variable rUA 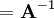 on line 2. Since
on line 2. Since 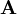 is diagonal, inversion is simply taking the reciprocals of the diagonal elements. Please note that the operation
is diagonal, inversion is simply taking the reciprocals of the diagonal elements. Please note that the operation .A() is the extraction of the 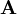 matrix from some other matrix divided by cell volumes as described in lines 639--663 of
matrix from some other matrix divided by cell volumes as described in lines 639--663 of src\finiteVolume\fvMatrices\fvMatrix\fvMatrix.C. Each diagonal element of 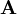 corresponds to a computational cell, so
corresponds to a computational cell, so 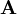 can be interpolated to the faces and is stored as the variable
can be interpolated to the faces and is stored as the variable rUAf 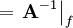 in line 3. As is done in Equations 26 and 27,
in line 3. As is done in Equations 26 and 27, 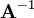 is then multiplied by the vector
is then multiplied by the vector 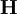 and stored as the variable
and stored as the variable U 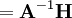 in line 5. It is called
in line 5. It is called U because, as Equation 26 shows, it is the contribution to the corrected velocity not including pressure and gravity. Please note that the operation .H() yields the same as the 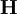 vector as described in lines 666--730 of
vector as described in lines 666--730 of src\finiteVolume\fvMatrices\fvMatrix\fvMatrix.C. Next, on lines 7--11, U is interpolated from the cell centers to the faces and dotted with the face surface normals where it becomes a flux and is hence called phiU 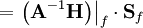 (flux is often denoted
(flux is often denoted phi in OpenFOAM). The + fvc::ddtPhiCorr(rUA, U, phi) part of this section of code "accounts for the divergence of the face velocity field by taking out the difference between the interpolated velocity and the flux." On line 13, the contribution from the gravity term is added to the flux forming the variable phi 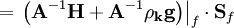 , which is the corrected velocity flux without the contribution of the pressure gradient.
, which is the corrected velocity flux without the contribution of the pressure gradient. phi is also the face-interpolated version of the quantity upon which the divergence operator is acting in the right-hand side of Equation 27.
Next, at line 15, a loop is entered in which pressure is corrected. This is a loop for the purpose of applying non-orthogonal correction, which will not be discussed here. Most importantly, lines 17--20 set up the Poisson equation for the pressure correction and can be seen to be the face-located analog to Equation 27. This shows that pressure is being predicted on the face, not the cell center. This procedure effectively applies Rhie-Chow interpolation which avoids the checkerboard pressure oscillations that can occur on a co-located grid as discussed on the CFD Online forum here. This Poisson equation is solved on line 24 or 28 yielding the first corrected pressure at the face, 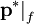 .
.
At line 33, pEqn.flux() is subtraced from the corrected velocity flux phi (which at this point does not include the pressure gradient contribution). pEqn.flux() appears to be 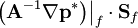 . In other words,
. In other words, phi 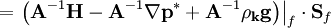 According to Equation 26, which is the cell-centered analog to the corrected velocity flux
According to Equation 26, which is the cell-centered analog to the corrected velocity flux phi, this is the final contribution to the corrected velocity flux.
At line 37, the corrected velocity flux is changed into a corrected cell-centered velocity. The quantity (phi - phiU)/rUAf) is ![\left[ \left. \left( \mathbf{A}^{-1} \mathbf{H} - \mathbf{A}^{-1} \mathbf{ \nabla p}^* + \mathbf{A}^{-1} \mathbf{\rho_k} \mathbf{g} \right) \right|_f \cdot \mathbf{S}_f - \left. \left( \mathbf{A}^{-1} \mathbf{H} \right) \right|_f \cdot \mathbf{S}_f \right] / \left. \mathbf{A}^{-1} \right|_f](/images/math/1/1/9/119751fa3146cf4b328869d49bf17c5b.png) which reduces to
which reduces to 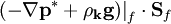 . Reconstructing this to the cell centers and multiplying by
. Reconstructing this to the cell centers and multiplying by rUA yields 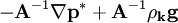 . The
. The tt += means that this quantity is then added onto the existing quantity for U which means that, finally, U 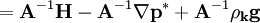 . This is the first corrected velocity
. This is the first corrected velocity 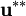 , it and agrees with Equation 26. Line 38 then updates the boundary conditions for velocity.
, it and agrees with Equation 26. Line 38 then updates the boundary conditions for velocity.
This entire process is repeated as many times as specified.
4 Modification for LES Capability
Following the more general turbulence implementation in pisoFoam, buoyantBoussinesqPisoFoam can be modified to not only incorporate a RANS turbulence model, but also LES models, or to run laminar. All modifications take place within the directory \applications\solvers\heatTransfer\buoyantBoussinesqPisoFoam.
First, the include section of buoyantBoussinesqPisoFoam.C is modified to appear as:
\*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "singlePhaseTransportModel.H" //#include "RASModel.H" //MJC 12-21-2009 #include "turbulenceModel.H" //MJC 12-21-2009 #include "fixedGradientFvPatchFields.H" //MJC 12-21-2009 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
Note that the comments //MJC 12-21-2009 are where I made changes.
Also in createFields.H the turbulence modeling section is changed to
Info<< "Creating turbulence model\n" << endl;
// autoPtr<incompressible::RASModel> turbulence //MJC 12-21-2009
// ( //MJC 12-21-2009
// incompressible::RASModel::New(U, phi, laminarTransport)//MJC 12-21-2009
// ); //MJC 12-21-2009
autoPtr<incompressible::turbulenceModel> turbulence //MJC 12-21-2009
( //MJC 12-21-2009
incompressible::turbulenceModel::New //MJC 12-21-2009
( //MJC 12-21-2009
U, //MJC 12-21-2009
phi, //MJC 12-21-2009
laminarTransport //MJC 12-21-2009
) //MJC 12-21-2009
); //MJC 12-21-2009Last, the Make/options file should now be
EXE_INC = \
-I$(LIB_SRC)/turbulenceModels \
-I$(LIB_SRC)/turbulenceModels/incompressible/turbulenceModel/lnInclude \
-I$(LIB_SRC)/transportModels \
-I$(LIB_SRC)/transportModels/incompressible/singlePhaseTransportModel \
-I$(LIB_SRC)/finiteVolume/lnInclude
EXE_LIBS = \
-lincompressibleRASModels \
-lincompressibleLESModels \
-lincompressibleTransportModels \
-lfiniteVolume \
-lmeshToolOnce these changes are made, type wmake from the \applications\solvers\heatTransfer\buoyantBoussinesqPisoFoam directory. To run the modified code, an additional file turbulenceProperties is needed inside the constant directory of your run in which you select RANS, LES, or laminar. If LES is selected, and LESProperties file is also needed. The turbulenceProperties file looks like
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: 1.6 | | \\ / A nd | Web: www.OpenFOAM.org | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object turbulenceProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // // simulationType RASModel; simulationType LESModel; // simulationType laminar; // ************************************************************************* //
5 References
- ↑ S. B. Pope, Turbulent Flows, Cambridge University Press, pp 581, 2001
- ↑ J. H. Ferziger and M. Peric, Computational Methods for Fluid Dynamics, 3rd, revised, Springer-Verlag, pp 14-15, 2002
- ↑ I. G. Currie, Fundamental Mechanics of Fluids, 2nd, Marcel Dekker, New York, NY, pp 18-22, 1993
- ↑ J. H. Ferziger and M. Peric, Computational Methods for Fluid Dynamics, 3rd, revised, Springer-Verlag, pp 9-10, 2002
- ↑ F. M. White, Viscous Fluid Flow, 2nd, McGraw-Hill, pp 73, 1991
- ↑ R. I. Issa, Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting, Journal of Computational Physics, 62, pp 40-65, 1985
- ↑ R. I. Issa, A. D. Gosman, and A. P. Watkins, The Computation of Compressible and Incompressible Recirculating Flow by a Non-Iterative Implicit Scheme, Journal of Computational Physics, 62, pp 66-82, 1986
- ↑ P. J. Oliveira and R. I. Issa, An Improved PISO Algorithm for the Computation of Buoyancy-Driven Flows, Numerical Heat Transfer, Part B, 40, pp 473-493, 2001
- ↑ H. Jasak, Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flow, PhD Thesis, Department of Mechanical Engineering, Imperial College of Science, Technology, and Medicine, London, pp 146-152, 1996
- ↑ J. H. Ferziger and M. Peric, Computational Methods for Fluid Dynamics, 3rd, revised, Springer-Verlag, pp 176, 2002
- ↑ P. J. Oliveira and R. I. Issa, An Improved PISO Algorithm for the Computation of Buoyancy-Driven Flows, Numerical Heat Transfer, Part B, 40, pp 473-493, 2001
- ↑ R. I. Issa, Solution of the Implicitly Discretized Fluid Flow Equations by Operator-Splitting, Journal of Computational Physics, 62, pp 40-65, 1985
- ↑ P. J. Oliveira and R. I. Issa, An Improved PISO Algorithm for the Computation of Buoyancy-Driven Flows, Numerical Heat Transfer, Part B, 40, pp 473-493, 2001
- ↑ OpenFOAM -- The Open Source CFD Toolbox, Programmer's Guide, Version 1.6, OpenCFD Ltd., 9 Albert Road, Caversham, Reading, Berkshire, Rg4 7AN, UK, pp 36, 2009
- ↑ OpenFOAM -- The Open Source CFD Toolbox, Programmer's Guide, Version 1.6, OpenCFD Ltd., 9 Albert Road, Caversham, Reading, Berkshire, Rg4 7AN, UK, pp 36, 2009