Contents
1 k-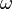 SST-SAS Equations
SST-SAS Equations
![\frac{\partial \omega}{\partial t}+\nabla \cdot (\vec{u}\omega) = \nabla^2[(\nu+\nu_t\sigma_\omega)\omega] + \frac{\gamma \omega}{k}\tau_{ij}\frac{\partial u_i}{\partial x_j}-\beta\omega^2 + 2(1-F_1)\sigma_{\omega2}\frac{1}{\omega}\nabla k \cdot \nabla \omega + P_{sas}](/images/math/8/f/d/8fdc71ed81184053161e14f340ebc6e9.png)
![\frac{\partial k}{\partial t}+\nabla \cdot (\vec{u}k) = \nabla^2[(\nu+\nu_t\sigma_k)k] + \tau_{ij}\frac{\partial u_i}{\partial x_j}-\beta^*\omega k](/images/math/9/4/9/949643430a76fff90a17aa73c6eb77ef.png)
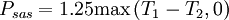
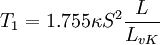
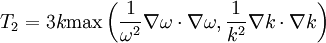
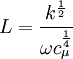
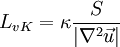
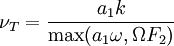
![F_2=\mbox{tanh} \left[ \left[ \mbox{max} \left( { 2 \sqrt{k} \over \beta^* \omega y } , { 500 \nu \over y^2 \omega } \right) \right]^2 \right]](/images/math/8/7/d/87d29560b46100813cef49e9f861f1cc.png)
![F_1=\mbox{tanh} \left\{ \left\{ \mbox{min} \left[ \mbox{max} \left( {\sqrt{k} \over \beta ^* \omega y}, {500 \nu \over y^2 \omega} \right) , {4 \sigma_{\omega 2} k \over CD_{k\omega} y^2} \right] \right\} ^4 \right\}](/images/math/1/4/3/1438132576e08de1da7394c694172485.png)
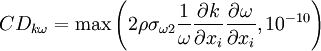
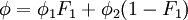
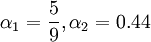
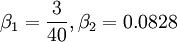
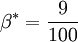
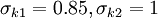
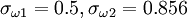
1.1 References
2 Solver
The openFoam solver is a modified version of turbFoam. Since the k-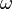 SST sas turbulence model, in unstable flow situations, gives LES-like solution fields, the modifications were introduced to handle the omega field and to allow the time averaging of pressure and velocity quantities. The averaging has been done in analogy with the openFoam LES solver oodles.
SST sas turbulence model, in unstable flow situations, gives LES-like solution fields, the modifications were introduced to handle the omega field and to allow the time averaging of pressure and velocity quantities. The averaging has been done in analogy with the openFoam LES solver oodles.
The solver files are available here: Media:turbFoamAverage.tar.gz
2.1 How to install the solver
3 Turbulence Model Files
Note: This library was obviously developed with 1.4.1 or older and won't compile with 1.5 or newer The turbulence models files are available here: Media:KOmegaTurbulenceModels.tar.gz
3.1 How to install the turbulence models files
4 Test Cases
4.1 Flow Past a Long Square Cylinder
Details about the test case are available at the ERCOFTAC NEXUS data base (ErcoftacLESig)
Test case files are available here:Media:LESigSquareCylSSTsas.tar.gz