Contrib/waves2Foam
From OpenFOAMWiki
1 waves2Foam
This web page will shortly contain information of how to use and download "waves2Foam".
The package is to be used in the modelling of free surface water waves. The package contains the following:
- Two libraries called convexPolyhedral and waves2Foam. See description below.
- Solver(s) to be used with 1.5 and 1.6+.
- Preprocessing tools to initialise the wave field in a domain and visualise the setup of the relaxation zone
- Tutorials on the use of waves2Foam
- Until later notice, a set of Matlab® functions are provided, which compute the needed wave parameters for the different wave theories
2 Distributed Libraries
- convexPolyhedral
- This library carries out intersection routines between faces/convex polyhedrals and the water surface given in terms of e.g. an algebraic equation such as
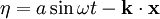 , where
, where 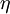 is the water surface elevation,
is the water surface elevation, 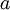 is the wave amplitude,
is the wave amplitude, 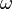 is the cyclic frequency,
is the cyclic frequency,  is time,
is time, 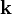 is the horizontal wave number vector, and
is the horizontal wave number vector, and 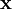 is a spatial coordinate.
is a spatial coordinate.
- waves2Foam
- This library contains implementations of wave theories, wave boundary conditions for
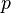 ,
, 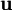 and
and 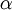 , being velocity, pressure and void-ratio respectively. Furthermore the library also contain the implementation of the relaxation zone technique, which is the method used for avoiding reflections from e.g. outlet boundaries. Finally it also contains an object to be used for initialising the velocity and void-ratio fields with e.g. an Airy wave.
, being velocity, pressure and void-ratio respectively. Furthermore the library also contain the implementation of the relaxation zone technique, which is the method used for avoiding reflections from e.g. outlet boundaries. Finally it also contains an object to be used for initialising the velocity and void-ratio fields with e.g. an Airy wave.
3 Dependencies
Besides the standard dependencies in OpenFoam, waves2Foam also depend on Gnu Scientific Library (GSL). This is needed for two reasons:
- In the cnoidal wave theory one has to evaluate Jacobian elliptic functions and complete elliptic integrals. These are not natively available in OpenFoam.
- A pre-processing tool, which is currently being developed, computes the needed wave parameters giving the minimal number of input parameters. This quickly results in a set of
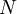 non-linear sets of equations in
non-linear sets of equations in 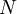 unknowns. For this purpose GSL is currently being used.
unknowns. For this purpose GSL is currently being used.
4 Download
At present the package is located on a non-public SVN. It will shortly be moved to a public SVN on SourceForge.