Contrib potentialWaveFoam
Contents
1 Short description
A one-line solver that solves a wave equation, fvm::d2dt2(phi) == c * c *fvc::laplacian(phi).
2 Overview
potentialWaveFoam solves a linear wave equation
(1) 
where  is a scalar variable,
is a scalar variable,  is time and
is time and  is the speed of wave
propagation (group velocity). If we take
is the speed of wave
propagation (group velocity). If we take  so that sound pressure
so that sound pressure 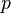 and acoustic particle velocity
and acoustic particle velocity  satisfy
satisfy
(2)  ,
,
(3)  ,
,
where 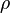 is the medium density, the wave equation is considered to
represent a linear sound propagation.
is the medium density, the wave equation is considered to
represent a linear sound propagation.
A boundary condition frequently used in linear acoustics is a normal
acousic impedance boundary condition. The normal acoustic impedance  is represented by sound pressure and the normal component of acoustic
particle velocity
is represented by sound pressure and the normal component of acoustic
particle velocity  as
as
 .
.
With substituting Eqs. (2) and (3), we obtain a convection equation of

(4) 
with the convective velocity  represented by
represented by
 .
.
For more detailed discussions, please have a look at reference [1].
3 Prerequisites
Python and funkySetFields are required to run the test case.
4 Package description and installation
4.1 Manifest
The package contains the following subdirectories:
potentialWaveFoam-YYYYMMDD/
convectiveOutlet-YYYYMMDD/ a convection BC code
potentialWaveFoam/ the main solver
probeToAudio/ a postprocessing utility
reverberationRoom/ a test case
4.2 Installation
Unpack the package under any suitable place under $WM_PROJECT_USER_DIR, e.g. $WM_PROJECT_USER_DIR/applications, go into the package directory and type ./Allrun.
cd $WM_PROJECT_USER_DIR/applications tar -zxf potentialWaveFoam-YYYYMMDD.tar.gz cd potentialWaveFoam-YYYYMMDD ./Allrun
These steps will install a library under $FOAM_USER_LIBBIN:
- libconvectiveOutlet.so - a BC code that calculates Eq. (4). For detailed usage, please see README under convectiveOutlet-YYYYMMDD in the package. The BC code can also be used as a nonreflective outlet BC for incompressible CFDs. Please also consult the reference [2] and a discussion at a forum thread if you intend to do so.
and applications under $FOAM_USER_APPBIN:
- potentialWaveFoam - the main solver that solves Eq. (1).
- probeToAudio - a postprocessing utility that converts probed sound pressure at a point to 16-bit PCM .wav audio format. For detailed usage, please have a look at the utility page.
and finally, a test case will be run.
5 Test case
The geometry of the test case provided under the reverberationRoom subdirectory is based on a Type II reverberation room owned by Kobayasi Institute of Physical Research [3], one of the most active civil acoustic research institutes in Japan, included under their permission. The room is used for measurements of airborne sound insulation performance of building elements conforming to ISO 140-1/3. A dummy open
window (represented by  ), however, is placed as a tested material in order to make reverberation time shorter for saving computational time and diffusers and absorbers usually installed for measurements are all removed for simplicity. Thus the case is not meant to be a reproduction of a real measurement situation.
), however, is placed as a tested material in order to make reverberation time shorter for saving computational time and diffusers and absorbers usually installed for measurements are all removed for simplicity. Thus the case is not meant to be a reproduction of a real measurement situation.
The problem solved is a propagation of a gaussian acoustic pulse placed at a point as an acoustic source. The walls other than the opening
are assigned an acoustic impedance of 136791.7 kg/(m2 s) which is equivalent to the
acoustic absorption factor  , given the relationship
, given the relationship
 .
.
The speed of sound  and the medium density
and the medium density 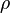 are assumed to be 343.7
m/s and 1.205 kg/m3 respectively.
are assumed to be 343.7
m/s and 1.205 kg/m3 respectively.
The solver will be run twice, with all the settings except endTime are
identical. A first run is for visualization of the initial propagation
of the acoustic pulse until  s, whose result can be viewed by
paraFoam as usual. Another run is for auralization of the impulse
response until
s, whose result can be viewed by
paraFoam as usual. Another run is for auralization of the impulse
response until  s recorded at a point in the room. After the
second run you will have an audible impulse response as p_1.wav under
the case directory, which should be heard as a gradually decaying
reverberation.
s recorded at a point in the room. After the
second run you will have an audible impulse response as p_1.wav under
the case directory, which should be heard as a gradually decaying
reverberation.
6 Cleanup
To cleanup the library/application build directories and the case directory, type
./Allclean
at the package directory.
7 Download
8 References
[1] T. Oshima et al., Proceedings of Inter-Noise 2008, No. 287, 2008
[2] J. H. Ferziger and M. Peric. Computational Methods for Fluid Dynamics. Springer-Verlag (Berlin), 1996
[3] http://www.kobayasi-riken.or.jp/english/english_frame_top.htm
9 History
7islands 12 October 2023 (Takuya OSHIMA): Provide a direct attachment to PotentialWaveFoam.tar.gz instead of a link.
7islands 08:22, 17 February 2009 (CET) (Takuya OSHIMA): Created this page.
