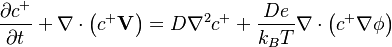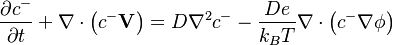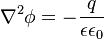Difference between revisions of "Extend-bazaar/solvers/multiphase/EHDIonFOAM"
(→Governing Equations) |
(→Governing Equations) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
:<math> \frac{\partial c^{+}}{\partial t} + \nabla \cdot \left(c^{+} \mathbf{V} \right) = D \nabla^2 c^{+} + \frac{ D e} {k_B T} \nabla \cdot \left( c^{+} \nabla \phi \right) </math> | :<math> \frac{\partial c^{+}}{\partial t} + \nabla \cdot \left(c^{+} \mathbf{V} \right) = D \nabla^2 c^{+} + \frac{ D e} {k_B T} \nabla \cdot \left( c^{+} \nabla \phi \right) </math> | ||
| − | :<math> \frac{\partial c^{-}}{\partial t} + \nabla \cdot \left(c^{-} \mathbf{V} \right) = D \nabla^2 c^{-} - \frac{ D e} {k_B T} \nabla \cdot \left( c^{ | + | :<math> \frac{\partial c^{-}}{\partial t} + \nabla \cdot \left(c^{-} \mathbf{V} \right) = D \nabla^2 c^{-} - \frac{ D e} {k_B T} \nabla \cdot \left( c^{-} \nabla \phi \right) </math> |
| + | |||
| + | :<math> \nabla^2 \phi = - \frac{q} {\epsilon \epsilon_{0}} </math> | ||
| + | |||
| + | Here, t is time; <math>\mathbf{v}</math> is the velocity field; <math>q=e(c^+ - c^-)</math> is the bulk charge density. | ||
| + | |||
| + | == Electrode Boundary Conditions == | ||
| + | |||
== Installation == | == Installation == | ||
Latest revision as of 02:52, 23 September 2019
Contents
1 Description
This code solves the continuity and momentum equations along with the transport equations for cations and anions and the Poisson equation. The electrostatic equations are coupled to the fluid flow equations through the convective terms in ionic transport equations. The ionic transport equations are coupled to each other through the electrostatic Poisson equation. This solver is written to address the internal electrohydrodynamic flow. However, since this code is developed from the InterFOAM solver, it can easily be used for the external electrohydrodynamic flow and can also address the multiphase flow.
The fixed gradient boundary condition library in OpenFOAM is modified to create a customized gradient boundary condition for the ions that can be updated in each iteration. This boundary conditions accounts for the flux of counter-ions at the electrode surface due to the faradaic reactions.
2 Governing Equations
These equations are under construction and not complete.
Here, t is time; 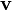 is the velocity field;
is the velocity field; 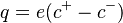 is the bulk charge density.
is the bulk charge density.
3 Electrode Boundary Conditions
4 Installation
Download from https://www.dropbox.com/sh/p45ax8p4qvgbsyu/AABJt38xa5ghHRvOLorv5WU_a?dl=0
Then compile by running:
cd EHDIonFOAM/
./wmake
5 Usage examples
To use this code, you have to create a channel that passes a fluid flow inside. A sample is given in page 31 of the following paper: Kashir et al (2019)
After creating the channel, you should specify the position of the electrodes in the channel. The discharge of counter-ions is already taken into account through the Boundary.H header file. The value of j here accounts for the flux of counter-ions and is found through dividing the measured electric current density at the electrode surface divided
Please have this mind that the channel flow is just a simple example. In reality electrostatic atomizers might have a hyperboloid structure. The only difference in complicated structures rather the sample channel flow presented in the paper is the complexity in grid creation. The usage of the EHDIonFOAM solver for understanding the electrification and charging mechanism inside electrostatic atomizers do not change.
6 Documentation
This implementation is based on the publication by Kashir et al (2019).
7 History
23 Sep 2019: First upload
![\rho \left[ \frac{\partial \mathbf{V}}{\partial t} + \left(\mathbf{V} \cdot \nabla \right) \mathbf{V} \right] = - \nabla p + \mu \nabla^2 \mathbf{V} +q \mathbf{E} + q \mathbf{E_{ext}}](/images/math/f/0/0/f004e4f9d81690bcffe459cb3e1fb244.png)