Difference between revisions of "FireFoam"
(→Evolution of Mass) |
(→Spices conservation: -> Species Conservation) |
||
| (39 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
==Solution Strategy== | ==Solution Strategy== | ||
| + | |||
| + | fireFoam is a solver which considers the evolution of particles, a liquid film on the surface of solid boundaries and the influence of pyrolysis within the framework of a compressible solver able to consider combustion and radiation. | ||
| + | |||
| + | The consideration of the particle and the liquid film leads to the capability to model the influence of sprinklers: The particle are leaving a nozzle. During the travelling towards the floor they change their speed do to the interaction with the surrounding air, their temperature and size due to energy exchange with the surrounding air and evaporation. When they hit a solid surface a liquid film is formed which flows in direction of the gravity and also exchanges energy with the surrounding fluid. | ||
| + | |||
| + | The consideration of pyrolysis leads to a more realistic modelling of the process leading to burnable substances when inflammable solids are present: Due to heat of combustion the chemical bounds of the solid are cut and gases are formed. During this process heat is generated and the gases are a new source of combustible for the flames. | ||
| + | |||
| + | Following this modelling purpose in fireFoam the general solution strategy is the following: | ||
| + | |||
| + | 1) First the particles are evolved in space and time. The coupling with the surrounding air is due the exchange of momentum (the feedback of the particle forces on the fluid is considered), exchange of energy and also mass (this is considered in the pressure equation of the fluid) | ||
| + | |||
| + | 2) The film is evolved in time: The coupling with the surrounding fluid is over the energy equation and due to the exchange of mass. For the film a separate region has to be created. | ||
| + | |||
| + | 3) The pyrolysis is solved (also here a separate region has to be created): The coupling to the air is only over the boundaries where energy (and probably also mass) can be exchanged. | ||
| + | |||
| + | 4) The fluid region is solve considering the evolution of momentum, energy (with radiation), spices and the pressure to enforce continuity. The pressure velocity coupling is achieved over a simple like algorithm. | ||
| + | |||
| + | Steps 1-4 are repeated until the desired time step is reached. | ||
| Line 180: | Line 198: | ||
</td><td width="5%">(x)</td></tr></table> | </td><td width="5%">(x)</td></tr></table> | ||
| − | <math> Sh</math>, <math> Sc </math>, <math> \tau_{p,k} = \rho_{p,k} d_p^2 / (18 \mu) </math> and <math> H_M </math> are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. <math> \rho_{p,k}</math> is the particle density and <math> \mu </math> the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number). | + | <math> Sh</math>, <math> Sc </math>, <math> \tau_{p,k} = \rho_{p,k} d_p^2 / (18 \mu) </math> and <math> H_M </math> are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. <math> \rho_{p,k}</math> is the particle density and <math> \mu </math> the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the mass transfer due to diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number). |
| + | In order to describe the relations used to calculate the evolution of the mass of a single droplet, the "liquidEvaporation" model is taken as an illustratory example. The starting point of this model is the relation found by Maxwell back in 1877 (see <ref> Sazhin, Sergei S. "Advanced models of fuel droplet heating and evaporation." Progress in energy and combustion science 32.2 (2006): 162-214. </ref> or https://www.researchgate.net/publication/222579979_Advanced_models_of_fuel_droplet_heating_and_evaporation) for the evaporation rate of a spherical droplet in a fluid at rest: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ d m_{p,k}}{d t} = - 2 \pi d_{p,k} k_{p,k} (\rho_{vs,k} - \rho_{v\infty,k}) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | Where <math> d_{p,k}, k_{p,k}, \rho_{vs,k}, \rho_{v\infty,k}</math> are the particle diameter of the spices k, the mass diffusivity of the spices k, the density of the vapour and the surface of the particle and far away, respectively. The density of the gas at the surface of the droplet is obtained by assuming that the pressure of gas surrounding the droplet is equal to the vapour pressure: <math> \rho_{vs,k} = p_{v,k} M_k / (R T_s) </math>. <math> p_{v,k} </math> , <math> M_k </math> and <math> T_s = (2 T_f + T_p)/3 </math> are the vapour pressure of the spices k, the molar weight of the same species and the temperature at the particle surface, respectively. For the calculation of the density of the vapour far away from the particle it is assumed that the temperature is equal to the particle surface temperature and the pressure is equal to the fluid pressure of the cell containing the particle: <math> \rho_{v\infty,k} = X_k p_{f} M_k / (R T_s) </math>. <math> X_k </math> and <math> \rho_{v\infty,k} = p_{f} </math> are the volume fraction of the species k computed in the cell containing the particle and the pressure of the cell containing the particle, respectively. Since above relation is only valid for fluids at rest, the whole relation is multiplied by the Ranz Marshall expression for the Sherwood number and after that we obtain: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ d m_{p,k}}{d t} = - (2 + 0.6Re^{1/2} Sc^{1/3}) \pi d_{p,k} k_{p,k} (\rho_{vs,k} - \rho_{v\infty,k}) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | The above relation gives for a vanishing Reynolds number Re the evaporation rate found by Maxwell. | ||
The source therm in the pressure and in the species equations of the carrier phase are calculated in src/lagrangian/intermediate/clouds/Templates/ReactingCloud/ReactingCloudI.H: | The source therm in the pressure and in the species equations of the carrier phase are calculated in src/lagrangian/intermediate/clouds/Templates/ReactingCloud/ReactingCloudI.H: | ||
| Line 601: | Line 639: | ||
<br><cpp> | <br><cpp> | ||
| + | |||
| + | template<class CloudType> | ||
| + | Foam::tmp<Foam::scalarField> Foam::LiquidEvaporation<CloudType>::calcXc | ||
| + | ( | ||
| + | const label celli | ||
| + | ) const | ||
| + | { | ||
| + | scalarField Xc(this->owner().thermo().carrier().Y().size()); | ||
| + | |||
| + | forAll(Xc, i) | ||
| + | { | ||
| + | Xc[i] = | ||
| + | this->owner().thermo().carrier().Y()[i][celli] | ||
| + | /this->owner().thermo().carrier().W(i); | ||
| + | } | ||
| + | |||
| + | return Xc/sum(Xc); | ||
| + | } | ||
| + | |||
| + | template<class CloudType> | ||
| + | Foam::scalar Foam::LiquidEvaporation<CloudType>::Sh | ||
| + | ( | ||
| + | const scalar Re, | ||
| + | const scalar Sc | ||
| + | ) const | ||
| + | { | ||
| + | return 2.0 + 0.6*Foam::sqrt(Re)*cbrt(Sc); | ||
| + | } | ||
| + | |||
| + | |||
template<class CloudType> | template<class CloudType> | ||
void Foam::LiquidEvaporation<CloudType>::calculate | void Foam::LiquidEvaporation<CloudType>::calculate | ||
| Line 684: | Line 752: | ||
====Evolution of Momentum==== | ====Evolution of Momentum==== | ||
| + | In order to calculate the evolution of the particle velocity the second Newton's law is solved: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | m_{p}\frac{ d u_{p}}{d t} = \sum F_p(u_p,u_f,C) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | Where <math> F_p(u_p,u_f) </math> and <math> u_p </math> are the forces acting on the particles (which are a function of the partilce velocity and | ||
| + | also the fluid velocity interpolated at particle position) and the particle velocity. <math> C </math> represent other parameters like gravity or the pressure gradient. The resulting ordinary differential equation can be solved with | ||
| + | standard methods. The list of particle | ||
| + | forces which can be chosen can be found in the folder srs/lagrangian/intermediate/submodels/Kinematic/ParticleForces/. | ||
====Evolution of Energy==== | ====Evolution of Energy==== | ||
| + | |||
| + | The equation for the particle Temperature is derived from the conservation of energy: | ||
| + | |||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ d H_{p}}{d t} = A_p \left ( \dot q _{conv} + \dot q_{abs} - \dot q_{em} \right ) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | It means that the change of the particle enthalpy <math> H_p </math> over time is equal to the heat transferred by convection <math> q _{conv} </math> plus the radiation heat | ||
| + | transferred from the surrounding to the particle <math> q _{abs} </math> minus the emitted radiation heat <math> q _{em} </math> . The above equation can be expressed | ||
| + | as function of the particle temperature <math> T_p </math>: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | m_p c_p \frac{ d T_{p}}{d t} = A_p \left ( h \left ( T_f - T_p \right ) + \dot q_{abs} - \sigma \epsilon T_p^4 \right ) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | <math> c_p </math> is the specific heat capacity of the particle, <math> T_f </math> the temperature of the surrounding gas, <math> h </math> the heat transfer | ||
| + | coefficient, <math> \sigma </math> the Boltzmann constant, <math> A_p </math> the particle surface and <math> \epsilon </math> the emissivity. Note that for a diffusive emitter (the radiation intensity <math> I </math> is equal for all directions) the radiation heat flux received can be expressed as <math> \dot q_{abs} = \epsilon \pi I </math> (see also https://en.wikipedia.org/wiki/Intensity_(heat_transfer)). The former relation leads with the definition of the in OpenFOAM of the incident radiation <math> G = 4 \pi I </math> (see also the thread https://www.cfd-online.com/Forums/openfoam-solving/178305-difference-between-idefault-g-radiation.html) to the final formulation of the temporal evolution | ||
| + | of the particle temperature: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | m_p c_p \frac{ d T_{p}}{d t} = A_p \left ( h \left ( T_f - T_p \right ) + \epsilon \frac{G}{4} - \sigma \epsilon T_p^4 \right ) | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | In order to get a relation of the heat transfer coefficient <math> h </math> the empirical derived relation for the Nusslet number of Ranz Marshall is used: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | h = \frac{Nu \kappa}{d_p} = \frac{(2 + 0.6\sqrt{Re}Pr^{1/3})\kappa}{d_p} | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | The soure code can be found in src/lagrangian/intermediate/parcels/Templates/ThermoParcel/ThermoParcel.C | ||
| + | <br><cpp> | ||
| + | |||
| + | template<class ParcelType> | ||
| + | template<class TrackCloudType> | ||
| + | Foam::scalar Foam::ThermoParcel<ParcelType>::calcHeatTransfer | ||
| + | ( | ||
| + | TrackCloudType& cloud, | ||
| + | trackingData& td, | ||
| + | const scalar dt, | ||
| + | const scalar Re, | ||
| + | const scalar Pr, | ||
| + | const scalar kappa, | ||
| + | const scalar NCpW, | ||
| + | const scalar Sh, | ||
| + | scalar& dhsTrans, | ||
| + | scalar& Sph | ||
| + | ) | ||
| + | { | ||
| + | if (!cloud.heatTransfer().active()) | ||
| + | { | ||
| + | return T_; | ||
| + | } | ||
| + | |||
| + | const scalar d = this->d(); | ||
| + | const scalar rho = this->rho(); | ||
| + | const scalar As = this->areaS(d); | ||
| + | const scalar V = this->volume(d); | ||
| + | const scalar m = rho*V; | ||
| + | |||
| + | // Calc heat transfer coefficient | ||
| + | scalar htc = cloud.heatTransfer().htc(d, Re, Pr, kappa, NCpW); | ||
| + | |||
| + | // Calculate the integration coefficients | ||
| + | const scalar bcp = htc*As/(m*Cp_); | ||
| + | const scalar acp = bcp*td.Tc(); | ||
| + | scalar ancp = Sh; | ||
| + | if (cloud.radiation()) | ||
| + | { | ||
| + | const tetIndices tetIs = this->currentTetIndices(); | ||
| + | const scalar Gc = td.GInterp().interpolate(this->coordinates(), tetIs); | ||
| + | const scalar sigma = physicoChemical::sigma.value(); | ||
| + | const scalar epsilon = cloud.constProps().epsilon0(); | ||
| + | |||
| + | ancp += As*epsilon*(Gc/4.0 - sigma*pow4(T_)); | ||
| + | } | ||
| + | ancp /= m*Cp_; | ||
| + | |||
| + | // Integrate to find the new parcel temperature | ||
| + | const scalar deltaT = cloud.TIntegrator().delta(T_, dt, acp + ancp, bcp); | ||
| + | const scalar deltaTncp = ancp*dt; | ||
| + | const scalar deltaTcp = deltaT - deltaTncp; | ||
| + | |||
| + | // Calculate the new temperature and the enthalpy transfer terms | ||
| + | scalar Tnew = T_ + deltaT; | ||
| + | Tnew = min(max(Tnew, cloud.constProps().TMin()), cloud.constProps().TMax()); | ||
| + | |||
| + | dhsTrans -= m*Cp_*deltaTcp; | ||
| + | |||
| + | Sph = dt*m*Cp_*bcp; | ||
| + | |||
| + | return Tnew; | ||
| + | } | ||
| + | </cpp><br> | ||
===Equations Liquid Film=== | ===Equations Liquid Film=== | ||
| Line 1,093: | Line 1,285: | ||
</cpp><br> | </cpp><br> | ||
| + | |||
| + | ===Pyrolysis=== | ||
| + | Pyrolysis is the thermal decomposition of materials at elevated temperatures in an inert atmosphere (https://en.wikipedia.org/wiki/Pyrolysis). | ||
| + | Its accurate description is important to obtain the composition of the gaseous volatiles. The composition of the gaseous volatiles is a matter of primary importance, since it determines the stability of the flame and the amount of soot that a flame will produce (https://www.researchgate.net/profile/Ashish_Vinayak/publication/322397262_Mathematical_Modeling_Simulation_of_Pyrolysis_Flame_Spread_in_OpenFOAM/links/5ab205ff0f7e9b4897c3d4c7/Mathematical-Modeling-Simulation-of-Pyrolysis-Flame-Spread-in-OpenFOAM.pdf). | ||
| + | |||
| + | In fireFoam the pyrolysis is treated as region model. The means that for each region where the pyrolysis has to be considered a different mesh has to be created on which the governing equations are solved. This equation are the mass, energy ans spices conservation. The coupling to the fluid region is achieved over the boundary conditions. | ||
| + | |||
| + | |||
| + | ====Mass conservation ==== | ||
| + | |||
| + | The mass conservation for the solid solved in fireFoam reads: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ \partial \rho}{\partial t} = R | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | <math> R</math> is the reaction rate ( or realise rate) of the gas. Note that here it is assumed that the volume of the pyrolysis zone remains constant. For the cases of a moving mesh (the pyrolysis zone gets smaller due release of gas) no mass conservation is solved and instead the density is kept constant. The vanishing of substance is accounted by the reduction of the size of the pyrolysis region. | ||
| + | |||
| + | The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C | ||
| + | |||
| + | <br><cpp> | ||
| + | void reactingOneDim::solveContinuity() | ||
| + | { | ||
| + | if (debug) | ||
| + | { | ||
| + | InfoInFunction << endl; | ||
| + | } | ||
| + | |||
| + | if (!moveMesh_) | ||
| + | { | ||
| + | fvScalarMatrix rhoEqn | ||
| + | ( | ||
| + | fvm::ddt(rho_) == -solidChemistry_->RRg() | ||
| + | ); | ||
| + | |||
| + | rhoEqn.solve(); | ||
| + | } | ||
| + | else | ||
| + | { | ||
| + | const scalarField deltaV | ||
| + | ( | ||
| + | -solidChemistry_->RRg()*regionMesh().V()*time_.deltaT()/rho_ | ||
| + | ); | ||
| + | |||
| + | updateMesh(deltaV); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | ==== Species Conservation ==== | ||
| + | |||
| + | In order to account for the chemical reactions occurring between different chemical species a conservation | ||
| + | equation for each species k has to be solved: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ \partial (\rho Y_k)}{\partial t} = R_k | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | <math> R_k</math> is the reaction rate of the species k. | ||
| + | |||
| + | The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C | ||
| + | |||
| + | <br><cpp> | ||
| + | void reactingOneDim::solveSpeciesMass() | ||
| + | { | ||
| + | if (debug) | ||
| + | { | ||
| + | InfoInFunction << endl; | ||
| + | } | ||
| + | |||
| + | volScalarField Yt(0.0*Ys_[0]); | ||
| + | |||
| + | for (label i=0; i<Ys_.size()-1; i++) | ||
| + | { | ||
| + | volScalarField& Yi = Ys_[i]; | ||
| + | |||
| + | fvScalarMatrix YiEqn | ||
| + | ( | ||
| + | fvm::ddt(rho_, Yi) == solidChemistry_->RRs(i) | ||
| + | ); | ||
| + | |||
| + | if (regionMesh().moving()) | ||
| + | { | ||
| + | surfaceScalarField phiYiRhoMesh | ||
| + | ( | ||
| + | fvc::interpolate(Yi*rho_)*regionMesh().phi() | ||
| + | ); | ||
| + | |||
| + | YiEqn -= fvc::div(phiYiRhoMesh); | ||
| + | |||
| + | } | ||
| + | |||
| + | YiEqn.solve(regionMesh().solver("Yi")); | ||
| + | Yi.max(0.0); | ||
| + | Yt += Yi; | ||
| + | } | ||
| + | |||
| + | Ys_[Ys_.size() - 1] = 1.0 - Yt; | ||
| + | |||
| + | } | ||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | ====Energy conservation==== | ||
| + | |||
| + | In the energy equation solved in the pyrolysis region, the conduction of heat in the solid is considered. Furthermore the heat realise due to the chemical reaction <math> \dot Q </math> and the loss of enthalpy by the solid due to the chemical reaction <math>\dot Q_s = \sum_i H_{s,i} R_i </math>: | ||
| + | |||
| + | <table width="70%"><tr><td> | ||
| + | <center><math> | ||
| + | |||
| + | \frac{ \partial (\rho h)}{\partial t} = \frac{ \partial (\kappa \partial h)}{\partial x_i \partial x_i} + \dot Q + \dot Q_s | ||
| + | |||
| + | </math></center> | ||
| + | </td><td width="5%">(x)</td></tr></table> | ||
| + | |||
| + | <math> \kappa </math> is the thermal conductivity. | ||
| + | |||
| + | The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C | ||
| + | |||
| + | <br><cpp> | ||
| + | |||
| + | void reactingOneDim::solveEnergy() | ||
| + | { | ||
| + | if (debug) | ||
| + | { | ||
| + | InfoInFunction << endl; | ||
| + | } | ||
| + | |||
| + | tmp<volScalarField> alpha(solidThermo_->alpha()); | ||
| + | |||
| + | fvScalarMatrix hEqn | ||
| + | ( | ||
| + | fvm::ddt(rho_, h_) | ||
| + | - fvm::laplacian(alpha, h_) | ||
| + | + fvc::laplacian(alpha, h_) | ||
| + | - fvc::laplacian(kappa(), T()) | ||
| + | == | ||
| + | chemistryQdot_ | ||
| + | + solidChemistry_->RRsHs() | ||
| + | ); | ||
| + | |||
| + | /* | ||
| + | NOTE: gas Hs is included in hEqn | ||
| + | |||
| + | if (gasHSource_) | ||
| + | { | ||
| + | const surfaceScalarField phiGas(fvc::interpolate(phiHsGas_)); | ||
| + | hEqn += fvc::div(phiGas); | ||
| + | } | ||
| + | */ | ||
| + | |||
| + | if (qrHSource_) | ||
| + | { | ||
| + | const surfaceScalarField phiqr(fvc::interpolate(qr_)*nMagSf()); | ||
| + | hEqn += fvc::div(phiqr); | ||
| + | } | ||
| + | |||
| + | /* | ||
| + | NOTE: The moving mesh option is only correct for reaction such as | ||
| + | Solid -> Gas, thus the ddt term is compesated exaclty by chemistrySh and | ||
| + | the mesh flux is not necessary. | ||
| + | |||
| + | if (regionMesh().moving()) | ||
| + | { | ||
| + | surfaceScalarField phihMesh | ||
| + | ( | ||
| + | fvc::interpolate(rho_*h_)*regionMesh().phi() | ||
| + | ); | ||
| + | |||
| + | hEqn -= fvc::div(phihMesh); | ||
| + | } | ||
| + | */ | ||
| + | hEqn.relax(); | ||
| + | hEqn.solve(); | ||
| + | } | ||
| + | |||
| + | </cpp><br> | ||
| + | |||
| + | ====Coupling between regions ==== | ||
===Equations Fluid=== | ===Equations Fluid=== | ||
| Line 1,492: | Line 1,872: | ||
</cpp><br> | </cpp><br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
=References= | =References= | ||
| − | |||
<references/> | <references/> | ||
Latest revision as of 20:06, 16 April 2021
fireFoam
Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling.
Contents
1 Solution Strategy
fireFoam is a solver which considers the evolution of particles, a liquid film on the surface of solid boundaries and the influence of pyrolysis within the framework of a compressible solver able to consider combustion and radiation.
The consideration of the particle and the liquid film leads to the capability to model the influence of sprinklers: The particle are leaving a nozzle. During the travelling towards the floor they change their speed do to the interaction with the surrounding air, their temperature and size due to energy exchange with the surrounding air and evaporation. When they hit a solid surface a liquid film is formed which flows in direction of the gravity and also exchanges energy with the surrounding fluid.
The consideration of pyrolysis leads to a more realistic modelling of the process leading to burnable substances when inflammable solids are present: Due to heat of combustion the chemical bounds of the solid are cut and gases are formed. During this process heat is generated and the gases are a new source of combustible for the flames.
Following this modelling purpose in fireFoam the general solution strategy is the following:
1) First the particles are evolved in space and time. The coupling with the surrounding air is due the exchange of momentum (the feedback of the particle forces on the fluid is considered), exchange of energy and also mass (this is considered in the pressure equation of the fluid)
2) The film is evolved in time: The coupling with the surrounding fluid is over the energy equation and due to the exchange of mass. For the film a separate region has to be created.
3) The pyrolysis is solved (also here a separate region has to be created): The coupling to the air is only over the boundaries where energy (and probably also mass) can be exchanged.
4) The fluid region is solve considering the evolution of momentum, energy (with radiation), spices and the pressure to enforce continuity. The pressure velocity coupling is achieved over a simple like algorithm.
Steps 1-4 are repeated until the desired time step is reached.
The source code can be found in fireFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | Copyright (C) 2011-2017 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application fireFoam Group grpCombustionSolvers Description Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "turbulentFluidThermoModel.H" #include "basicReactingCloud.H" #include "surfaceFilmModel.H" #include "pyrolysisModelCollection.H" #include "radiationModel.H" #include "SLGThermo.H" #include "solidChemistryModel.H" #include "psiReactionThermo.H" #include "CombustionModel.H" #include "pimpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Transient solver for fires and turbulent diffusion flames" " with reacting particle clouds, surface film and pyrolysis modelling." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" #include "createTimeControls.H" #include "compressibleCourantNo.H" #include "setInitialDeltaT.H" #include "createRegionControls.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (runTime.run()) { #include "readTimeControls.H" #include "compressibleCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setMultiRegionDeltaT.H" #include "setDeltaT.H" ++runTime; Info<< "Time = " << runTime.timeName() << nl << endl; parcels.evolve(); surfaceFilm.evolve(); if(solvePyrolysisRegion) { pyrolysis.evolve(); } if (solvePrimaryRegion) { #include "rhoEqn.H" // --- PIMPLE loop while (pimple.loop()) { #include "UEqn.H" #include "YEEqn.H" // --- Pressure corrector loop while (pimple.correct()) { #include "pEqn.H" } if (pimple.turbCorr()) { turbulence->correct(); } } rho = thermo.rho(); } runTime.write(); runTime.printExecutionTime(Info); } Info<< "End" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Equations Parcels
The particles in fireFoam are treated in a Lagrangian frame of reference. This means that each particle (or parcel which is an ensemble of a number of particles with the same properties) is tracked individually throughout the computational domain. For each parcel a ordinary differential equation is solved which describes the evolution of its mass, velocity (after one integration more also the position in space) and its temperature. The evolution of the particle mass is required besides for its own momentum equation to calculate the mass source term in the spices and the pressure equation of the carrier phase. The particle momentum equation through which the particle velocity and after one integration also the particle position is obtained, is required to calculate the forces acting from the particles on the carrier phase required in the momentum equation of the fluid. The energy equation of the particles (the temperature is obtained by an equation of state) is required to compute the source term due to the particles in the energy equation of the carrier phase. Note that some additional informations can be also found in https://www.politesi.polimi.it/bitstream/10589/134603/7/2017_07_Ghasemi.pdf and http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2013/EmilLjungskog/reactingParcelFilmFoam_report.pdf.
2.1.1 Evolution of Mass
According to [1] (see also https://trs.jpl.nasa.gov/bitstream/handle/2014/22473/97-0966.pdf?sequence=1)
the evaporating mass of a spherical droplet with the diameter 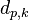 and mass
and mass 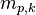 (the subscript k denotes the spices k since in OpenFOAM different spices can be tracked) can be expressed in the following form:
(the subscript k denotes the spices k since in OpenFOAM different spices can be tracked) can be expressed in the following form:
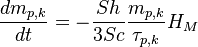 | (x) |
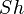 ,
, 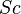 ,
, 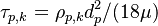 and
and 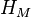 are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively.
are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. 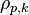 is the particle density and
is the particle density and  the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the mass transfer due to diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number).
In order to describe the relations used to calculate the evolution of the mass of a single droplet, the "liquidEvaporation" model is taken as an illustratory example. The starting point of this model is the relation found by Maxwell back in 1877 (see [2] or https://www.researchgate.net/publication/222579979_Advanced_models_of_fuel_droplet_heating_and_evaporation) for the evaporation rate of a spherical droplet in a fluid at rest:
the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the mass transfer due to diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number).
In order to describe the relations used to calculate the evolution of the mass of a single droplet, the "liquidEvaporation" model is taken as an illustratory example. The starting point of this model is the relation found by Maxwell back in 1877 (see [2] or https://www.researchgate.net/publication/222579979_Advanced_models_of_fuel_droplet_heating_and_evaporation) for the evaporation rate of a spherical droplet in a fluid at rest:
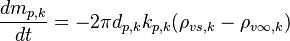 | (x) |
Where 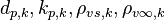 are the particle diameter of the spices k, the mass diffusivity of the spices k, the density of the vapour and the surface of the particle and far away, respectively. The density of the gas at the surface of the droplet is obtained by assuming that the pressure of gas surrounding the droplet is equal to the vapour pressure:
are the particle diameter of the spices k, the mass diffusivity of the spices k, the density of the vapour and the surface of the particle and far away, respectively. The density of the gas at the surface of the droplet is obtained by assuming that the pressure of gas surrounding the droplet is equal to the vapour pressure: 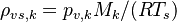 .
. 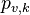 ,
, 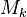 and
and 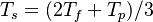 are the vapour pressure of the spices k, the molar weight of the same species and the temperature at the particle surface, respectively. For the calculation of the density of the vapour far away from the particle it is assumed that the temperature is equal to the particle surface temperature and the pressure is equal to the fluid pressure of the cell containing the particle:
are the vapour pressure of the spices k, the molar weight of the same species and the temperature at the particle surface, respectively. For the calculation of the density of the vapour far away from the particle it is assumed that the temperature is equal to the particle surface temperature and the pressure is equal to the fluid pressure of the cell containing the particle: 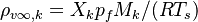 .
. 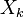 and
and 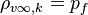 are the volume fraction of the species k computed in the cell containing the particle and the pressure of the cell containing the particle, respectively. Since above relation is only valid for fluids at rest, the whole relation is multiplied by the Ranz Marshall expression for the Sherwood number and after that we obtain:
are the volume fraction of the species k computed in the cell containing the particle and the pressure of the cell containing the particle, respectively. Since above relation is only valid for fluids at rest, the whole relation is multiplied by the Ranz Marshall expression for the Sherwood number and after that we obtain:
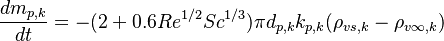 | (x) |
The above relation gives for a vanishing Reynolds number Re the evaporation rate found by Maxwell.
The source therm in the pressure and in the species equations of the carrier phase are calculated in src/lagrangian/intermediate/clouds/Templates/ReactingCloud/ReactingCloudI.H:
template<class CloudType> inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> Foam::ReactingCloud<CloudType>::Srho(const label i) const { tmp<volScalarField::Internal> tRhoi ( new volScalarField::Internal ( IOobject ( this->name() + ":rhoTrans", this->db().time().timeName(), this->db(), IOobject::NO_READ, IOobject::NO_WRITE, false ), this->mesh(), dimensionedScalar ( rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero ) ) ); if (this->solution().coupled()) { scalarField& rhoi = tRhoi.ref(); rhoi = rhoTrans_[i]/(this->db().time().deltaTValue()*this->mesh().V()); } return tRhoi; } template<class CloudType> inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> Foam::ReactingCloud<CloudType>::Srho() const { tmp<volScalarField::Internal> trhoTrans ( new volScalarField::Internal ( IOobject ( this->name() + ":rhoTrans", this->db().time().timeName(), this->db(), IOobject::NO_READ, IOobject::NO_WRITE, false ), this->mesh(), dimensionedScalar ( rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero ) ) ); if (this->solution().coupled()) { scalarField& sourceField = trhoTrans.ref(); forAll(rhoTrans_, i) { sourceField += rhoTrans_[i]; } sourceField /= this->db().time().deltaTValue()*this->mesh().V(); } return trhoTrans; }
The field rhoTrans_ is modified in the file src/lagrangian/intermediate/parcels/Templates/ReactingParcel/ReactingParcel.C:
template<class ParcelType> template<class TrackCloudType> void Foam::ReactingParcel<ParcelType>::calc ( TrackCloudType& cloud, trackingData& td, const scalar dt ) { const auto& composition = cloud.composition(); // Define local properties at beginning of time step // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ const scalar np0 = this->nParticle_; const scalar d0 = this->d_; const vector& U0 = this->U_; const scalar T0 = this->T_; const scalar mass0 = this->mass(); // Calc surface values scalar Ts, rhos, mus, Prs, kappas; this->calcSurfaceValues(cloud, td, T0, Ts, rhos, mus, Prs, kappas); scalar Res = this->Re(rhos, U0, td.Uc(), d0, mus); // Sources // ~~~~~~~ // Explicit momentum source for particle vector Su = Zero; // Linearised momentum source coefficient scalar Spu = 0.0; // Momentum transfer from the particle to the carrier phase vector dUTrans = Zero; // Explicit enthalpy source for particle scalar Sh = 0.0; // Linearised enthalpy source coefficient scalar Sph = 0.0; // Sensible enthalpy transfer from the particle to the carrier phase scalar dhsTrans = 0.0; // 1. Compute models that contribute to mass transfer - U, T held constant // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // Phase change // ~~~~~~~~~~~~ // Mass transfer due to phase change scalarField dMassPC(Y_.size(), 0.0); // Molar flux of species emitted from the particle (kmol/m^2/s) scalar Ne = 0.0; // Sum Ni*Cpi*Wi of emission species scalar NCpW = 0.0; // Surface concentrations of emitted species scalarField Cs(composition.carrier().species().size(), 0.0); // Calc mass and enthalpy transfer due to phase change calcPhaseChange ( cloud, td, dt, Res, Prs, Ts, mus/rhos, d0, T0, mass0, 0, 1.0, Y_, dMassPC, Sh, Ne, NCpW, Cs ); // 2. Update the parcel properties due to change in mass // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ scalarField dMass(dMassPC); scalar mass1 = updateMassFraction(mass0, dMass, Y_); this->Cp_ = composition.Cp(0, Y_, td.pc(), T0); // Update particle density or diameter if (cloud.constProps().constantVolume()) { this->rho_ = mass1/this->volume(); } else { this->d_ = cbrt(mass1/this->rho_*6.0/pi); } // Remove the particle when mass falls below minimum threshold if (np0*mass1 < cloud.constProps().minParcelMass()) { td.keepParticle = false; if (cloud.solution().coupled()) { scalar dm = np0*mass0; // Absorb parcel into carrier phase forAll(Y_, i) { scalar dmi = dm*Y_[i]; label gid = composition.localToCarrierId(0, i); scalar hs = composition.carrier().Hs(gid, td.pc(), T0); cloud.rhoTrans(gid)[this->cell()] += dmi; cloud.hsTrans()[this->cell()] += dmi*hs; } cloud.UTrans()[this->cell()] += dm*U0; cloud.phaseChange().addToPhaseChangeMass(np0*mass1); } return; } // Correct surface values due to emitted species correctSurfaceValues(cloud, td, Ts, Cs, rhos, mus, Prs, kappas); Res = this->Re(rhos, U0, td.Uc(), this->d(), mus); // 3. Compute heat- and momentum transfers // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // Heat transfer // ~~~~~~~~~~~~~ // Calculate new particle temperature this->T_ = this->calcHeatTransfer ( cloud, td, dt, Res, Prs, kappas, NCpW, Sh, dhsTrans, Sph ); this->Cp_ = composition.Cp(0, Y_, td.pc(), T0); // Motion // ~~~~~~ // Calculate new particle velocity this->U_ = this->calcVelocity(cloud, td, dt, Res, mus, mass1, Su, dUTrans, Spu); // 4. Accumulate carrier phase source terms // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ if (cloud.solution().coupled()) { // Transfer mass lost to carrier mass, momentum and enthalpy sources forAll(dMass, i) { scalar dm = np0*dMass[i]; label gid = composition.localToCarrierId(0, i); scalar hs = composition.carrier().Hs(gid, td.pc(), T0); cloud.rhoTrans(gid)[this->cell()] += dm; cloud.UTrans()[this->cell()] += dm*U0; cloud.hsTrans()[this->cell()] += dm*hs; } // Update momentum transfer cloud.UTrans()[this->cell()] += np0*dUTrans; cloud.UCoeff()[this->cell()] += np0*Spu; // Update sensible enthalpy transfer cloud.hsTrans()[this->cell()] += np0*dhsTrans; cloud.hsCoeff()[this->cell()] += np0*Sph; // Update radiation fields if (cloud.radiation()) { const scalar ap = this->areaP(); const scalar T4 = pow4(T0); cloud.radAreaP()[this->cell()] += dt*np0*ap; cloud.radT4()[this->cell()] += dt*np0*T4; cloud.radAreaPT4()[this->cell()] += dt*np0*ap*T4; } } }
The evaporation model is called in the file src/lagrangian/intermediate/parcels/Templates/ReactingParcel/ReactingParcel.C:
template<class ParcelType> template<class TrackCloudType> void Foam::ReactingParcel<ParcelType>::calcPhaseChange ( TrackCloudType& cloud, trackingData& td, const scalar dt, const scalar Re, const scalar Pr, const scalar Ts, const scalar nus, const scalar d, const scalar T, const scalar mass, const label idPhase, const scalar YPhase, const scalarField& Y, scalarField& dMassPC, scalar& Sh, scalar& N, scalar& NCpW, scalarField& Cs ) { const auto& composition = cloud.composition(); auto& phaseChange = cloud.phaseChange(); if (!phaseChange.active() || (YPhase < SMALL)) { return; } scalarField X(composition.liquids().X(Y)); scalar Tvap = phaseChange.Tvap(X); if (T < Tvap) { return; } const scalar TMax = phaseChange.TMax(td.pc(), X); const scalar Tdash = min(T, TMax); const scalar Tsdash = min(Ts, TMax); // Calculate mass transfer due to phase change phaseChange.calculate ( dt, this->cell(), Re, Pr, d, nus, Tdash, Tsdash, td.pc(), td.Tc(), X, dMassPC ); // Limit phase change mass by availability of each specie dMassPC = min(mass*YPhase*Y, dMassPC); const scalar dMassTot = sum(dMassPC); // Add to cumulative phase change mass phaseChange.addToPhaseChangeMass(this->nParticle_*dMassTot); forAll(dMassPC, i) { const label cid = composition.localToCarrierId(idPhase, i); const scalar dh = phaseChange.dh(cid, i, td.pc(), Tdash); Sh -= dMassPC[i]*dh/dt; } // Update molar emissions if (cloud.heatTransfer().BirdCorrection()) { // Average molecular weight of carrier mix - assumes perfect gas const scalar Wc = td.rhoc()*RR*td.Tc()/td.pc(); forAll(dMassPC, i) { const label cid = composition.localToCarrierId(idPhase, i); const scalar Cp = composition.carrier().Cp(cid, td.pc(), Tsdash); const scalar W = composition.carrier().W(cid); const scalar Ni = dMassPC[i]/(this->areaS(d)*dt*W); const scalar Dab = composition.liquids().properties()[i].D(td.pc(), Tsdash, Wc); // Molar flux of species coming from the particle (kmol/m^2/s) N += Ni; // Sum of Ni*Cpi*Wi of emission species NCpW += Ni*Cp*W; // Concentrations of emission species Cs[cid] += Ni*d/(2.0*Dab); } } }
For the case the "liquidEvaporation" model is used the function calculate of this specific model is called in the file src/lagrangian/submodels/Reacting/PhaseChangeModel/LiquidEvaporation/LiquidEvaporation.C:
template<class CloudType> Foam::tmp<Foam::scalarField> Foam::LiquidEvaporation<CloudType>::calcXc ( const label celli ) const { scalarField Xc(this->owner().thermo().carrier().Y().size()); forAll(Xc, i) { Xc[i] = this->owner().thermo().carrier().Y()[i][celli] /this->owner().thermo().carrier().W(i); } return Xc/sum(Xc); } template<class CloudType> Foam::scalar Foam::LiquidEvaporation<CloudType>::Sh ( const scalar Re, const scalar Sc ) const { return 2.0 + 0.6*Foam::sqrt(Re)*cbrt(Sc); } template<class CloudType> void Foam::LiquidEvaporation<CloudType>::calculate ( const scalar dt, const label celli, const scalar Re, const scalar Pr, const scalar d, const scalar nu, const scalar T, const scalar Ts, const scalar pc, const scalar Tc, const scalarField& X, scalarField& dMassPC ) const { // immediately evaporate mass that has reached critical condition if ((liquids_.Tc(X) - T) < SMALL) { if (debug) { WarningInFunction << "Parcel reached critical conditions: " << "evaporating all available mass" << endl; } forAll(activeLiquids_, i) { const label lid = liqToLiqMap_[i]; dMassPC[lid] = GREAT; } return; } // construct carrier phase species volume fractions for cell, celli const scalarField Xc(calcXc(celli)); // calculate mass transfer of each specie in liquid forAll(activeLiquids_, i) { const label gid = liqToCarrierMap_[i]; const label lid = liqToLiqMap_[i]; // vapour diffusivity [m2/s] const scalar Dab = liquids_.properties()[lid].D(pc, Ts); // saturation pressure for species i [pa] // - carrier phase pressure assumed equal to the liquid vapour pressure // close to the surface // NOTE: if pSat > pc then particle is superheated // calculated evaporation rate will be greater than that of a particle // at boiling point, but this is not a boiling model const scalar pSat = liquids_.properties()[lid].pv(pc, T); // Schmidt number const scalar Sc = nu/(Dab + ROOTVSMALL); // Sherwood number const scalar Sh = this->Sh(Re, Sc); // mass transfer coefficient [m/s] const scalar kc = Sh*Dab/(d + ROOTVSMALL); // vapour concentration at surface [kmol/m3] at film temperature const scalar Cs = pSat/(RR*Ts); // vapour concentration in bulk gas [kmol/m3] at film temperature const scalar Cinf = Xc[gid]*pc/(RR*Ts); // molar flux of vapour [kmol/m2/s] const scalar Ni = max(kc*(Cs - Cinf), 0.0); // mass transfer [kg] dMassPC[lid] += Ni*pi*sqr(d)*liquids_.properties()[lid].W()*dt; } }
2.1.2 Evolution of Momentum
In order to calculate the evolution of the particle velocity the second Newton's law is solved:
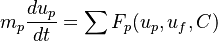 | (x) |
Where 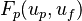 and
and 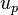 are the forces acting on the particles (which are a function of the partilce velocity and
also the fluid velocity interpolated at particle position) and the particle velocity.
are the forces acting on the particles (which are a function of the partilce velocity and
also the fluid velocity interpolated at particle position) and the particle velocity. 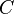 represent other parameters like gravity or the pressure gradient. The resulting ordinary differential equation can be solved with
standard methods. The list of particle
forces which can be chosen can be found in the folder srs/lagrangian/intermediate/submodels/Kinematic/ParticleForces/.
represent other parameters like gravity or the pressure gradient. The resulting ordinary differential equation can be solved with
standard methods. The list of particle
forces which can be chosen can be found in the folder srs/lagrangian/intermediate/submodels/Kinematic/ParticleForces/.
2.1.3 Evolution of Energy
The equation for the particle Temperature is derived from the conservation of energy:
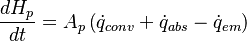 | (x) |
It means that the change of the particle enthalpy 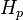 over time is equal to the heat transferred by convection
over time is equal to the heat transferred by convection 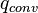 plus the radiation heat
transferred from the surrounding to the particle
plus the radiation heat
transferred from the surrounding to the particle 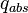 minus the emitted radiation heat
minus the emitted radiation heat 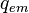 . The above equation can be expressed
as function of the particle temperature
. The above equation can be expressed
as function of the particle temperature 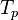 :
:
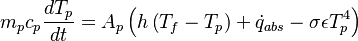 | (x) |
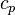 is the specific heat capacity of the particle,
is the specific heat capacity of the particle, 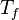 the temperature of the surrounding gas,
the temperature of the surrounding gas, 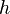 the heat transfer
coefficient,
the heat transfer
coefficient, 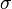 the Boltzmann constant,
the Boltzmann constant, 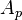 the particle surface and
the particle surface and  the emissivity. Note that for a diffusive emitter (the radiation intensity
the emissivity. Note that for a diffusive emitter (the radiation intensity 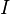 is equal for all directions) the radiation heat flux received can be expressed as
is equal for all directions) the radiation heat flux received can be expressed as 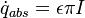 (see also https://en.wikipedia.org/wiki/Intensity_(heat_transfer)). The former relation leads with the definition of the in OpenFOAM of the incident radiation
(see also https://en.wikipedia.org/wiki/Intensity_(heat_transfer)). The former relation leads with the definition of the in OpenFOAM of the incident radiation 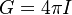 (see also the thread https://www.cfd-online.com/Forums/openfoam-solving/178305-difference-between-idefault-g-radiation.html) to the final formulation of the temporal evolution
of the particle temperature:
(see also the thread https://www.cfd-online.com/Forums/openfoam-solving/178305-difference-between-idefault-g-radiation.html) to the final formulation of the temporal evolution
of the particle temperature:
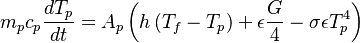 | (x) |
In order to get a relation of the heat transfer coefficient 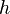 the empirical derived relation for the Nusslet number of Ranz Marshall is used:
the empirical derived relation for the Nusslet number of Ranz Marshall is used:
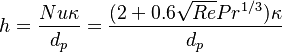 | (x) |
The soure code can be found in src/lagrangian/intermediate/parcels/Templates/ThermoParcel/ThermoParcel.C
template<class ParcelType> template<class TrackCloudType> Foam::scalar Foam::ThermoParcel<ParcelType>::calcHeatTransfer ( TrackCloudType& cloud, trackingData& td, const scalar dt, const scalar Re, const scalar Pr, const scalar kappa, const scalar NCpW, const scalar Sh, scalar& dhsTrans, scalar& Sph ) { if (!cloud.heatTransfer().active()) { return T_; } const scalar d = this->d(); const scalar rho = this->rho(); const scalar As = this->areaS(d); const scalar V = this->volume(d); const scalar m = rho*V; // Calc heat transfer coefficient scalar htc = cloud.heatTransfer().htc(d, Re, Pr, kappa, NCpW); // Calculate the integration coefficients const scalar bcp = htc*As/(m*Cp_); const scalar acp = bcp*td.Tc(); scalar ancp = Sh; if (cloud.radiation()) { const tetIndices tetIs = this->currentTetIndices(); const scalar Gc = td.GInterp().interpolate(this->coordinates(), tetIs); const scalar sigma = physicoChemical::sigma.value(); const scalar epsilon = cloud.constProps().epsilon0(); ancp += As*epsilon*(Gc/4.0 - sigma*pow4(T_)); } ancp /= m*Cp_; // Integrate to find the new parcel temperature const scalar deltaT = cloud.TIntegrator().delta(T_, dt, acp + ancp, bcp); const scalar deltaTncp = ancp*dt; const scalar deltaTcp = deltaT - deltaTncp; // Calculate the new temperature and the enthalpy transfer terms scalar Tnew = T_ + deltaT; Tnew = min(max(Tnew, cloud.constProps().TMin()), cloud.constProps().TMax()); dhsTrans -= m*Cp_*deltaTcp; Sph = dt*m*Cp_*bcp; return Tnew; }
2.2 Equations Liquid Film
The equation describing the evolution of the liquid film can be found in http://www.ilasseurope.org/ICLASS/iclass2012_Heidelberg/Contributions/Paper-pdfs/Contribution1294_b.pdf and https://www.witpress.com/Secure/elibrary/papers/MPF11/MPF11020FU1.pdf. A description of the method used to derive the equation can be found in https://www.researchgate.net/profile/Petr_Vita/publication/313655371_Thin_Film_Fluid_Flow_Simulation_on_Rotating_Discs/links/58a1a592a6fdccf5e9707665/Thin-Film-Fluid-Flow-Simulation-on-Rotating-Discs.pdf.
2.2.1 Mass Conservation Film
The conservation of mass reads:
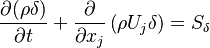 | (1) |
 represents the mean film velocity,
represents the mean film velocity, 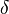 the film height and
the film height and 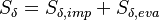 the mass source term resulting
from the impingement of the liquid droplets on the film surface
the mass source term resulting
from the impingement of the liquid droplets on the film surface 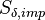 and due to the evaporation of the film
and due to the evaporation of the film 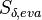 . Note
that the source term due to evaporation
. Note
that the source term due to evaporation 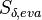 will be inserted into the pressure equation for the gas phase and also into the equation for the spices
transport.
The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
will be inserted into the pressure equation for the gas phase and also into the equation for the spices
transport.
The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveContinuity() { if (debug) { InfoInFunction << endl; } solve ( fvm::ddt(deltaRho_) + fvc::div(phi_) == - rhoSp_ ); }
2.2.2 Momentum Conservation Film
The momentum conservation reads:
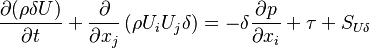 | (2) |
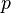 represents the pressure,
represents the pressure, 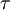 the stress like components of the forces acting on the filme and
the stress like components of the forces acting on the filme and 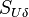 represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects
represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects 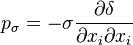 , the hydrostatic contribution
, the hydrostatic contribution 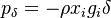 and the contribution of the pressure originated by the surrounding gas
and the contribution of the pressure originated by the surrounding gas 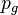 .
. 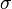 represents the surface tension. The stress like contribution is divided in the wall shear stress
represents the surface tension. The stress like contribution is divided in the wall shear stress 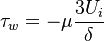 , the gravity force tangential to the wall
, the gravity force tangential to the wall 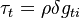 and the contribution of the contact line force
and the contribution of the contact line force 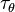 .
. 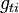 is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
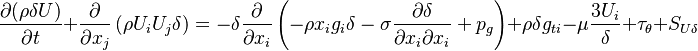 | (3) |
The source code of the momentum equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
tmp<Foam::fvVectorMatrix> kinematicSingleLayer::solveMomentum ( const volScalarField& pu, const volScalarField& pp ) { if (debug) { InfoInFunction << endl; } // Momentum tmp<fvVectorMatrix> tUEqn ( fvm::ddt(deltaRho_, U_) + fvm::div(phi_, U_) == - USp_ // - fvm::SuSp(rhoSp_, U_) - rhoSp_*U_ + forces_.correct(U_) + turbulence_->Su(U_) ); fvVectorMatrix& UEqn = tUEqn.ref(); UEqn.relax(); if (momentumPredictor_) { solve ( UEqn == fvc::reconstruct ( - fvc::interpolate(delta_) * ( regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) + fvc::snGrad(delta_)*fvc::interpolate(pp) ) - fvc::flux(rho_*gTan()) ) ) ); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); } return tUEqn; }
2.2.3 Energy Conservation Film
The energy equation reads:
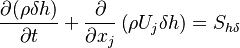 | (4) |
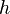 represents the mean film enthalpy and
represents the mean film enthalpy and  represents the contribution of the impinging droplets
represents the contribution of the impinging droplets 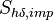 and the evaporation of the film
and the evaporation of the film 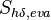 to the
energy equation. Note that the energy required by the film (or a portion of it) to evaporate
to the
energy equation. Note that the energy required by the film (or a portion of it) to evaporate  is cast as source term into the energy equation of the surrounding gas. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
is cast as source term into the energy equation of the surrounding gas. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
void thermoSingleLayer::solveEnergy() { if (debug) { InfoInFunction << endl; } dimensionedScalar residualDeltaRho ( "residualDeltaRho", deltaRho_.dimensions(), 1e-10 ); solve ( fvm::ddt(deltaRho_, hs_) + fvm::div(phi_, hs_) == - hsSp_ + q(hs_) + radiation_->Shs() ); correctThermoFields(); // Evaluate viscosity from user-model viscosity_->correct(pPrimary_, T_); // Update film wall and surface temperatures updateSurfaceTemperatures(); }
2.2.4 Film Thickness Equation
The last equation missing is the linear equation used to get the film thickness 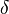 . In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P
. In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P 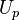 which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
![\rho \bold {U_p} \delta = \rho \left [ \bold { H[U] } \bold {\frac {1}{A_P}} - \bold {\frac {1}{A_P}}\delta \nabla \left ( \underbrace{-\rho g_i x_i}_{P_p} \delta - \underbrace{\sigma \nabla \nabla \delta + p_g}_{P_u} \right ) + \bold {\frac {1}{A_P}}\rho \delta g_t \right ] \delta](/images/math/1/4/4/1449081c4710027a4a917a67b76e63d8.png) | (5) |
The operator ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the
contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
![\rho \nabla \cdot \left ( \bold {U_p} \delta \right ) =
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \bold {\frac {\delta}{A_P}} \nabla \left ( {P_p} \delta +{P_u} \right ) + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right )](/images/math/d/0/1/d01b1ab158ed586aad40b8a661609dd0.png) | (6) |
The above equation can be inserted into the continuity equation to obtain:
![\frac{ \partial (\rho \delta )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {\delta^2}{A_P} \nabla {P_p} - \frac {\delta P_p}{A_P} \nabla {\delta} - \bold {\frac {\delta}{A_P}} \nabla {P_u} + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right ) = S_{\delta}](/images/math/a/7/5/a75cca6b4eadbbd675d0306542636176.png) | (7) |
It is obvious that the above equation is non linear in 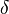 . In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
. In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k P_p}{A_P} \nabla {\delta^{k+1}} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) = S_{\delta}](/images/math/5/4/f/54f1c220c3827744789ebcd9820f8f4b.png) | (8) |
The superscript k denote the solution computed at the last iteration an the superscript k+1 denotes the solution of the current iteration which has to be computed by solving the linear system resulting from the discretization. After separating the linear and the still non linear terms of the above equation we obtain:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k+1} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/8/2/3/823a63f544781d33fd0bacc9b5ba0531.png) | (9) |
Since the above equation still contains a non linear contribution it has remaining 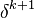 has to be approximated by the value at the previous iteration step
has to be approximated by the value at the previous iteration step
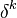 :
:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/f/c/b/fcb9c168d16e87fc3f62d76c091541b5.png) | (10) |
which is the final form solved in the present solver. The source code can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveThickness ( const volScalarField& pu, const volScalarField& pp, const fvVectorMatrix& UEqn ) { if (debug) { InfoInFunction << endl; } volScalarField rUA(1.0/UEqn.A()); U_ = rUA*UEqn.H(); surfaceScalarField deltarUAf(fvc::interpolate(delta_*rUA)); surfaceScalarField rhof(fvc::interpolate(rho_)); surfaceScalarField phiAdd ( "phiAdd", regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) ) - fvc::flux(rho_*gTan()) ); constrainFilmField(phiAdd, 0.0); surfaceScalarField phid ( "phid", fvc::flux(U_*rho_) - deltarUAf*phiAdd*rhof ); constrainFilmField(phid, 0.0); surfaceScalarField ddrhorUAppf ( "deltaCoeff", fvc::interpolate(delta_)*deltarUAf*rhof*fvc::interpolate(pp) ); regionMesh().setFluxRequired(delta_.name()); for (int nonOrth=0; nonOrth<=nNonOrthCorr_; nonOrth++) { // Film thickness equation fvScalarMatrix deltaEqn ( fvm::ddt(rho_, delta_) + fvm::div(phid, delta_) - fvm::laplacian(ddrhorUAppf, delta_) == - rhoSp_ ); deltaEqn.solve(); if (nonOrth == nNonOrthCorr_) { phiAdd += fvc::interpolate(pp) * fvc::snGrad(delta_) * regionMesh().magSf(); phi_ == deltaEqn.flux(); } } // Bound film thickness by a minimum of zero delta_.max(0.0); // Update U field U_ -= fvc::reconstruct(deltarUAf*phiAdd); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); // Update film wall and surface velocities updateSurfaceVelocities(); // Continuity check continuityCheck(); }
2.2.5 Solution Strategy
Equations (1), (3) and (4) represent a system of 3 non-linear partial differential equations with the unknowns 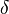 ,
, 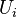 and
and 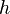 . In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
. In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
1. Solve continuity equation (1). Here has to be mentioned that the quantity solved for is 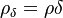 which appears also in the momentum and energy equation.
which appears also in the momentum and energy equation.
2. Solve momentum equation (3)
3. Solve energy equation (4)
4. Solve film thickness equation: The film thickness equation is derived by inserting the discrete momentum equation into the continuity equation.
Steps 2-4 are solved a number of time specified by the user in order to achieve sufficient convergence of the equations. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer
void thermoSingleLayer::evolveRegion() { if (debug) { InfoInFunction << endl; } // Solve continuity for deltaRho_ solveContinuity(); // Update sub-models to provide updated source contributions updateSubmodels(); // Solve continuity for deltaRho_ solveContinuity(); for (int oCorr=1; oCorr<=nOuterCorr_; oCorr++) { // Explicit pressure source contribution tmp<volScalarField> tpu(this->pu()); // Implicit pressure source coefficient tmp<volScalarField> tpp(this->pp()); // Solve for momentum for U_ tmp<fvVectorMatrix> UEqn = solveMomentum(tpu(), tpp()); // Solve energy for hs_ - also updates thermo solveEnergy(); // Film thickness correction loop for (int corr=1; corr<=nCorr_; corr++) { // Solve thickness for delta_ solveThickness(tpu(), tpp(), UEqn()); } } // Update deltaRho_ with new delta_ deltaRho_ == delta_*rho_; // Update temperature using latest hs_ T_ == T(hs_); }
2.3 Pyrolysis
Pyrolysis is the thermal decomposition of materials at elevated temperatures in an inert atmosphere (https://en.wikipedia.org/wiki/Pyrolysis). Its accurate description is important to obtain the composition of the gaseous volatiles. The composition of the gaseous volatiles is a matter of primary importance, since it determines the stability of the flame and the amount of soot that a flame will produce (https://www.researchgate.net/profile/Ashish_Vinayak/publication/322397262_Mathematical_Modeling_Simulation_of_Pyrolysis_Flame_Spread_in_OpenFOAM/links/5ab205ff0f7e9b4897c3d4c7/Mathematical-Modeling-Simulation-of-Pyrolysis-Flame-Spread-in-OpenFOAM.pdf).
In fireFoam the pyrolysis is treated as region model. The means that for each region where the pyrolysis has to be considered a different mesh has to be created on which the governing equations are solved. This equation are the mass, energy ans spices conservation. The coupling to the fluid region is achieved over the boundary conditions.
2.3.1 Mass conservation
The mass conservation for the solid solved in fireFoam reads:
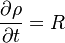 | (x) |
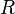 is the reaction rate ( or realise rate) of the gas. Note that here it is assumed that the volume of the pyrolysis zone remains constant. For the cases of a moving mesh (the pyrolysis zone gets smaller due release of gas) no mass conservation is solved and instead the density is kept constant. The vanishing of substance is accounted by the reduction of the size of the pyrolysis region.
is the reaction rate ( or realise rate) of the gas. Note that here it is assumed that the volume of the pyrolysis zone remains constant. For the cases of a moving mesh (the pyrolysis zone gets smaller due release of gas) no mass conservation is solved and instead the density is kept constant. The vanishing of substance is accounted by the reduction of the size of the pyrolysis region.
The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C
void reactingOneDim::solveContinuity() { if (debug) { InfoInFunction << endl; } if (!moveMesh_) { fvScalarMatrix rhoEqn ( fvm::ddt(rho_) == -solidChemistry_->RRg() ); rhoEqn.solve(); } else { const scalarField deltaV ( -solidChemistry_->RRg()*regionMesh().V()*time_.deltaT()/rho_ ); updateMesh(deltaV); } }
2.3.2 Species Conservation
In order to account for the chemical reactions occurring between different chemical species a conservation equation for each species k has to be solved:
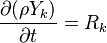 | (x) |
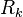 is the reaction rate of the species k.
is the reaction rate of the species k.
The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C
void reactingOneDim::solveSpeciesMass() { if (debug) { InfoInFunction << endl; } volScalarField Yt(0.0*Ys_[0]); for (label i=0; i<Ys_.size()-1; i++) { volScalarField& Yi = Ys_[i]; fvScalarMatrix YiEqn ( fvm::ddt(rho_, Yi) == solidChemistry_->RRs(i) ); if (regionMesh().moving()) { surfaceScalarField phiYiRhoMesh ( fvc::interpolate(Yi*rho_)*regionMesh().phi() ); YiEqn -= fvc::div(phiYiRhoMesh); } YiEqn.solve(regionMesh().solver("Yi")); Yi.max(0.0); Yt += Yi; } Ys_[Ys_.size() - 1] = 1.0 - Yt; }
2.3.3 Energy conservation
In the energy equation solved in the pyrolysis region, the conduction of heat in the solid is considered. Furthermore the heat realise due to the chemical reaction  and the loss of enthalpy by the solid due to the chemical reaction
and the loss of enthalpy by the solid due to the chemical reaction 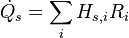 :
:
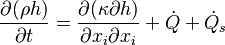 | (x) |
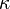 is the thermal conductivity.
is the thermal conductivity.
The source code can be found in src/regionModels/pyrolysisModels/reactingOneDim/reactingOneDim.C
void reactingOneDim::solveEnergy() { if (debug) { InfoInFunction << endl; } tmp<volScalarField> alpha(solidThermo_->alpha()); fvScalarMatrix hEqn ( fvm::ddt(rho_, h_) - fvm::laplacian(alpha, h_) + fvc::laplacian(alpha, h_) - fvc::laplacian(kappa(), T()) == chemistryQdot_ + solidChemistry_->RRsHs() ); /* NOTE: gas Hs is included in hEqn if (gasHSource_) { const surfaceScalarField phiGas(fvc::interpolate(phiHsGas_)); hEqn += fvc::div(phiGas); } */ if (qrHSource_) { const surfaceScalarField phiqr(fvc::interpolate(qr_)*nMagSf()); hEqn += fvc::div(phiqr); } /* NOTE: The moving mesh option is only correct for reaction such as Solid -> Gas, thus the ddt term is compesated exaclty by chemistrySh and the mesh flux is not necessary. if (regionMesh().moving()) { surfaceScalarField phihMesh ( fvc::interpolate(rho_*h_)*regionMesh().phi() ); hEqn -= fvc::div(phihMesh); } */ hEqn.relax(); hEqn.solve(); }
2.3.4 Coupling between regions
2.4 Equations Fluid
2.4.1 Mass conservation
The variable-density continuity equation is
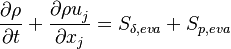 | (11) |
The source terms in the mass conservation equations come from the evaporation of the liquid film 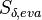 and from
the liquid droplets
and from
the liquid droplets 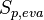 .
.
The source code can be found in rhoEqn.H:
{ fvScalarMatrix rhoEqn ( fvm::ddt(rho) + fvc::div(phi) == parcels.Srho(rho) + surfaceFilm.Srho() + fvOptions(rho) ); rhoEqn.solve(); fvOptions.correct(rho); }
2.4.2 Momentum conservation
The equation of motion are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
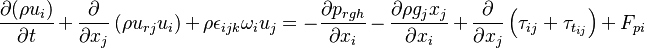 | (12) |
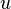 represent the velocity,
represent the velocity, 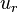 the relative veloicty,
the relative veloicty, 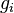 the gravitational acceleration,
the gravitational acceleration, 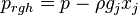 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
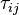 and
and 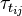 are the viscose and turbulent stresses. Note that since the relative velocity
are the viscose and turbulent stresses. Note that since the relative velocity 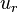 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux  appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
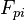 represents the force excreted by the particles on the fluid.
represents the force excreted by the particles on the fluid.
The source code can be found in Ueqn.H:
MRF.correctBoundaryVelocity(U);
fvVectorMatrix UEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence->divDevRhoReff(U)
==
parcels.SU(U)
+ fvOptions(rho, U)
);
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}
2.4.3 Species conservation
In order to account for the chemical reactions occurring between different chemical species a conservation equation for each species k has to be solved:
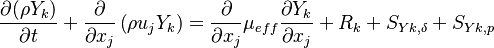 | (13) |
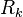 is the reaction rate of the species k and
is the reaction rate of the species k and 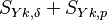 is the contribution to the spices k by the evaporation of the film and the particle respectively.
is the contribution to the spices k by the evaporation of the film and the particle respectively.
The source code can be found in YEEqn.H:
tmp<fv::convectionScheme<scalar>> mvConvection ( fv::convectionScheme<scalar>::New ( mesh, fields, phi, mesh.divScheme("div(phi,Yi_h)") ) ); { combustion->correct(); Qdot = combustion->Qdot(); volScalarField Yt(0.0*Y[0]); forAll(Y, i) { if (i != inertIndex && composition.active(i)) { volScalarField& Yi = Y[i]; fvScalarMatrix YiEqn ( fvm::ddt(rho, Yi) + mvConvection->fvmDiv(phi, Yi) - fvm::laplacian(turbulence->alphaEff(), Yi) == parcels.SYi(i, Yi) + surfaceFilm.Srho(i) + combustion->R(Yi) + fvOptions(rho, Yi) ); YiEqn.relax(); fvOptions.constrain(YiEqn); YiEqn.solve(mesh.solver("Yi")); fvOptions.correct(Yi); Yi.max(0.0); Yt += Yi; } } Y[inertIndex] = scalar(1) - Yt; Y[inertIndex].max(0.0); radiation->correct();
2.4.4 Energy conservation
The derivation of the energy equation (without source terms from the evaporation of the particle  and the liquid film
and the liquid film 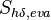 ) can be found in: https://cfd.direct/openfoam/energy-equation/
) can be found in: https://cfd.direct/openfoam/energy-equation/
The total energy of a fluid element can be seen as the sum of kinetic energy 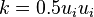 and internal energy
and internal energy  .
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
.
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
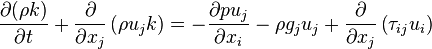 | (14) |
The rate of change of the internal energy  of a fluid element is the heat transferred to this fluid element by diffusion and turbulence
of a fluid element is the heat transferred to this fluid element by diffusion and turbulence 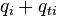 plus the
heat source term
plus the
heat source term  plus the heat source by radiation
plus the heat source by radiation 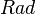 :
:
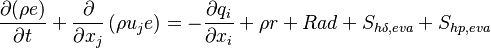 | (15) |
The change rate of the total energy is the sum of the above two equations:
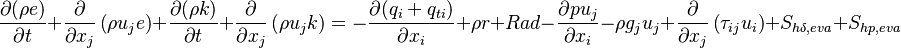 | (16) |
Instead of the internal energy  there is also the option to solve the equation for the enthalpy
there is also the option to solve the equation for the enthalpy 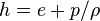 :
:
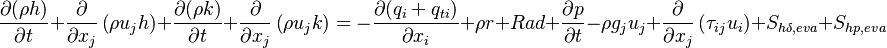 | (17) |
The source code can be found in YEEqn.H:
volScalarField& he = thermo.he();
fvScalarMatrix EEqn
(
fvm::ddt(rho, he) + mvConvection->fvmDiv(phi, he)
+ fvc::ddt(rho, K) + fvc::div(phi, K)
+ (
he.name() == "e"
? fvc::div
(
fvc::absolute(phi/fvc::interpolate(rho), U),
p,
"div(phiv,p)"
)
: -dpdt
)
- fvm::laplacian(turbulence->alphaEff(), he)
==
Qdot
+ radiation->Sh(thermo, he)
+ parcels.Sh(he)
+ surfaceFilm.Sh()
+ fvOptions(rho, he)
);
EEqn.relax();
fvOptions.constrain(EEqn);
EEqn.solve();
fvOptions.correct(he);
thermo.correct();
Info<< "min/max(T) = "
<< min(T).value() << ", " << max(T).value() << endl;
2.4.5 Pressure equation
As most of the solvers of OpenFOAM also fireFoam is a pressure based solver. In this class of solvers, the discrete momentum equation (which contains also the pressure gradient) is used to obtain a semi discrete equation for the velocity at the cell centre. This velocity is cast into the continuity equation in order to obtain an equation for the pressure which satisfies the mass conservation and by construction also the momentum equation. It has also to be mentioned, that the pressure equation which is solved, is only valid for law Mach number flows, i.e., it is assumed that the density has only a weak dependency from the pressure. Large temperature variation are however allowed (see the difference to the pressure equation solved in https://openfoamwiki.net/index.php/ChtMultiRegionFoam).
Starting point for the derivation of the pressure equation is the discrete continuity equation after integrating over the control volume:
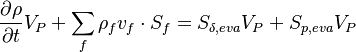 | (18) |
The subscript f denotes the the quantities are evaluated at the cell faces. The semi discrete momentum equation reads:
![\bold{A_P U_P} - \bold {H[U]} = - \nabla p_{rgh,P} - g \cdot x \nabla \rho](/images/math/1/d/b/1db5afd48eed9f3b7e872a3b3f58aaf6.png) | (19) |
and after rearranging with respect to the velocity at the cell centre 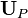 :
:
![\bold{ U_P} = \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho}{\bold A_P}](/images/math/a/c/2/ac2c0b09ce13348e276a799ac7dfdf74.png) | (20) |
and
are the contribution of the off diagonal elements of the matrix and the diagonal elements of the matrix, respectively.
The above equation can be inserted into the continuity equation:
![\frac{ \partial \rho}{\partial t} V_P + \sum_f \rho_f \left ( \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho}{\bold A_P} \right )_f \cdot S_f = S_{\delta,eva}V_P + S_{p,eva}V_P](/images/math/2/2/4/224f0fd6b344158c7d56bf102aa02aa0.png) | (21) |
Since the above equation still contains the density a relation between the density and the pressure is required. In the most general form it can be expressed as:
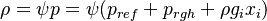 | (22) |
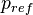 is the reference pressure.
is the reference pressure.
If we insert equation (22) into equation (21) we get a non-linear equation for the pressure when evaluating the divergence (the second term in equation (21)). However, if we assume only a week dependence of the density from the pressure, the density at the previous iteration 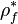 can be taken as a reasonable approximation of the
density at the current iteration step
can be taken as a reasonable approximation of the
density at the current iteration step 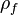 . Since we can still have a strong variation of the density with time (in turbulent combustion the temperature is highly in-stationary and hence also the density varies considerably with time) the temporal derivatives have to be kept. The resulting equation reads:
. Since we can still have a strong variation of the density with time (in turbulent combustion the temperature is highly in-stationary and hence also the density varies considerably with time) the temporal derivatives have to be kept. The resulting equation reads:
![\frac{ \partial \psi ( p_{ref} + p_{rgh} + \rho^* g_i x_i )}{\partial t} V_P + \sum_f \rho_f^* \left ( \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho^*}{\bold A_P} \right )_f \cdot S_f = S_{\delta,eva}V_P + S_{p,eva}V_P](/images/math/4/2/f/42fcc28e9376fa5f554c8c92fad2b295.png) | (23) |
The source code can be found in pEqn.H:
rho = thermo.rho(); volScalarField rAU(1.0/UEqn.A()); surfaceScalarField rhorAUf("rhorAUf", fvc::interpolate(rho*rAU)); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); surfaceScalarField phig("phig", -rhorAUf*ghf*fvc::snGrad(rho)*mesh.magSf()); surfaceScalarField phiHbyA ( "phiHbyA", ( fvc::flux(rho*HbyA) + MRF.zeroFilter(rhorAUf*fvc::ddtCorr(rho, U, phi)) ) + phig ); MRF.makeRelative(fvc::interpolate(rho), phiHbyA); // Update the pressure BCs to ensure flux consistency constrainPressure(p_rgh, rho, U, phiHbyA, rhorAUf, MRF); while (pimple.correctNonOrthogonal()) { fvScalarMatrix p_rghEqn ( fvm::ddt(psi, p_rgh) + fvc::ddt(psi, rho)*gh + fvc::ddt(psi)*pRef + fvc::div(phiHbyA) - fvm::laplacian(rhorAUf, p_rgh) == parcels.Srho() + surfaceFilm.Srho() + fvOptions(psi, p_rgh, rho.name()) ); p_rghEqn.solve(mesh.solver(p_rgh.select(pimple.finalInnerIter()))); if (pimple.finalNonOrthogonalIter()) { phi = phiHbyA + p_rghEqn.flux(); U = HbyA + rAU*fvc::reconstruct((p_rghEqn.flux() + phig)/rhorAUf); U.correctBoundaryConditions(); fvOptions.correct(U); } } p = p_rgh + rho*gh + pRef; #include "rhoEqn.H" #include "compressibleContinuityErrs.H" K = 0.5*magSqr(U); if (thermo.dpdt()) { dpdt = fvc::ddt(p); }
3 References
- ↑ Miller, R. S., K. Harstad, and J. Bellan. "Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations." International Journal of Multiphase Flow 24.6 (1998): 1025-1055.
- ↑ Sazhin, Sergei S. "Advanced models of fuel droplet heating and evaporation." Progress in energy and combustion science 32.2 (2006): 162-214.