Howto simpleMatrixLeastSquareFit
This is a very simple example of how to use the simpleMatrix class to solve a vector-matrix system using the LUsolve functionality
It does not require any dictionaries. I called it clduFoam and I execute it using 'clduFoam -e0 0 -e0 1'.
The values used to fit the function are hardcoded because I wanted to keep it simple
1 Code
Application
clduFoam
// base functions
// 0 - 1
// 1 - 1.0/T
// 2 - log(T)
// 3 - T^e
Description
\*---------------------------------------------------------------------------*/
#include "fvCFD.H"
#include "simpleMatrix.H"
#include "OFstream.H"
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
// Main program:
int main(int argc, char *argv[])
{
argList::validOptions.insert("e0", "scalar");
argList::validOptions.insert("e1", "scalar");
# include "setRootCase.H"
// number of data-points
label N = 4;
// number of base functions
label Nc = 4;
// number of e-values between e0 and e1
label Ne = 10;
simpleMatrix<scalar> A(Nc);
scalarField coeffs(Nc);
scalar e0 = atof(args.options()["e0"].c_str());
scalar e1 = atof(args.options()["e1"].c_str());
scalar de = (e1-e0)/(Ne-1);
scalarField T(N);
scalarField pv(N);
scalarField w(N);
T[0] = 340.0; pv[0] = 0.133; w[0] = 5.0;
T[1] = 368.0; pv[1] = 1.33; w[1] = 1.0;
T[2] = 465.0; pv[2] = 1.0e+5; w[2] = 100.0;
T[3] = 700.0; pv[3] = 1.0e+8; w[3] = 1.0e-0;
scalarField logPv(log(pv));
scalarField logT(log(T));
scalarField Tinv(1.0/T);
for(label it=0; it<Ne; it++)
{
scalar e = e0 + it*de;
scalarField powT(pow(T,e));
A.source()[0] = sum(logPv*w);
A.source()[1] = sum(logPv*Tinv*w);
A.source()[2] = sum(logPv*logT*w);
A.source()[3] = sum(logPv*powT*w);
A[0][0] = sum(w);
A[0][1] = sum(Tinv*w);
A[0][2] = sum(logT*w);
A[0][3] = sum(powT*w);
A[1][0] = sum(Tinv*w);
A[1][1] = sum(Tinv*Tinv*w);
A[1][2] = sum(logT*Tinv*w);
A[1][3] = sum(powT*Tinv*w);
A[2][0] = sum(logT*w);
A[2][1] = sum(Tinv*logT*w);
A[2][2] = sum(logT*logT*w);
A[2][3] = sum(powT*logT*w);
A[3][0] = sum(powT*w);
A[3][1] = sum(Tinv*powT*w);
A[3][2] = sum(logT*powT*w);
A[3][3] = sum(powT*powT*w);
coeffs = A.LUsolve();
//Info << coeffs << endl;
scalar err = 0.0;
forAll(T,i)
{
scalar pc = coeffs[0] + coeffs[1]/T[i] + coeffs[2]*::log(T[i]) + coeffs[3]*::pow(T[i],e);
err += ::pow(pc - logPv[i], 2);
pc = ::exp(pc);
}
cout.precision(12);
Info << "e = " << e << ", err = " << ::sqrt(err) << ",c = " << coeffs << endl;
}
forAll(T,i)
{
scalar pc = coeffs[0] + coeffs[1]/T[i] + coeffs[2]*::log(T[i]) + coeffs[3]*::pow(T[i],e1);
pc = ::exp(pc);
Info << "T = " << T[i] << ", pv = " << pv[i] << ", pvFit = " << pc << endl;
}
OFstream dataFile
(
"val.dat"
);
for(scalar Ti=300; Ti <= 710; Ti +=1)
{
scalar logpc = coeffs[0] + coeffs[1]/Ti + coeffs[2]*::log(Ti) + coeffs[3]*::pow(Ti,e1);
scalar pc = ::exp(logpc);
dataFile << Ti << " " << logpc << " " << pc << endl;
}
Info << "End\n" << endl;
return 0;
}
// ************************************************************************* //
2 Description
I want to do a curve-fit of the function
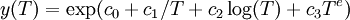
to a number of 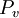 values.
values.
I want to minimize the function
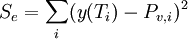
with respect to the coefficients 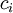 .
.
But since the function is an exp, I will minimize the difference in log instead, i.e.
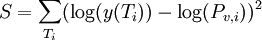
Hence
![\frac{\partial S}{\partial c_i} = \frac{\partial}{\partial c_i}\sum_{T_i} [c_0 + c_1/T_i + c_2\log(T_i) + c_3T_i^e - log(P_{v,i})]^2 = 0](/images/math/f/d/c/fdc27ac0b10160a8d3e4abf4533d383c.png) .
.
and we get
![\frac{\partial S}{\partial c_0} = 2\sum_{T_i} \{ [c_0 + c_1/T_i + c_2\log(T_i) + c_3T_i^e - log(P_{v,i})] \} = 0](/images/math/4/e/3/4e33c969b34863bf1bd82a0b7071718b.png)
![\frac{\partial S}{\partial c_1} = 2\sum_{T_i} \{ [c_0 + c_1/T_i + c_2\log(T_i) + c_3T_i^e - log(P_{v,i})] (1/T_i)\} = 0](/images/math/6/4/b/64be870ffa79995411ec7c7644c8dd4c.png)
![\frac{\partial S}{\partial c_2} = 2\sum_{T_i} \{ [c_0 + c_1/T_i + c_2\log(T_i) + c_3T_i^e - log(P_{v,i})] \log(T_i)\} = 0](/images/math/c/2/c/c2c6452e05eb4b6062a9439caef86bc8.png)
![\frac{\partial S}{\partial c_3} = 2\sum_{T_i} \{ [c_0 + c_1/T_i + c_2\log(T_i) + c_3T_i^e - log(P_{v,i})] T_i^e\} = 0](/images/math/5/3/7/5378fc7e8cf0e2c89f930c3304f1a435.png)
which we can write as a vector matrix system 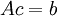
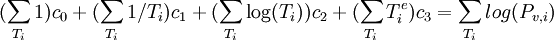
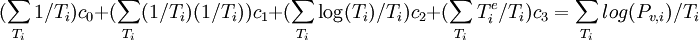
et c. The matrix components should be clear from the code, where weigths have also been added.
--Niklas 07:56, 21 January 2009 (CET)