OpenFOAM guide/Matrices in OpenFOAM
Linear equations resulting from the discretization method are solved in OpenFOAM using matrix methods. OpenFOAM has a specialized strategy for handling these matrices.
Contents
1 Overview
The discretization process results in the equation:
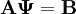
Where:
- A is the discretization matrix, which holds the matrix coefficients;
-
 is the vector array of variables being solved for; and
is the vector array of variables being solved for; and
- B is the discretization source term.
The A component is an N x N square matrix, where N is the number of equations produced by the discretization process. OpenFOAM has developed a specialized strategy to handle this matrix. Important components of this strategy include:
- lduMatrix (lower - diagonal - upper - matrix storage class); and
- lduAddressing (an indexing class);
- fvMatrix (contains components specific to the finite volume method).
2 lduMatrix
The lduMatrix class stores the matrix coefficients in three arrays:
scalarField *lowerPtr_; scalarField *diagPtr_; scalarField *upperPtr_;
These arrays are Fields that contain all the non-zero entries in the coefficient matrix.
The access of the coefficients goes over the functions:
scalarField& upper() scalarField& lower() scalarField& diag()
The size of the arrays lowerPtr_ and upperPtr_ are equal to the number of internal faces. The size of the array diagPtr_ is equal to the number of cells.
2.1 Diagonals
Every cell has one and only one diagonal coefficient, none of which are zero. Therefore the diagonal list contains N values, where N is the number of cells in the mesh. These are denoted:
- As discretization coefficients,
 ; or
; or
- As matrix coefficients,
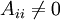 .
.
2.2 Upper and lower triangles
The upper and lower triangles have (N - 1)N possible values, however most are zero. The non-zero values correspond to cell-pairs that influence one another. OpenFOAM uses a small computational molecule, therefore only adjacent cells influence one another. In other words, there are two non-zero coefficients for every internal face in the mesh: one that appears in the lower triangle; and one that appears in the upper triangle.
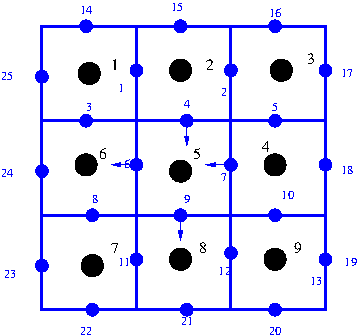
For instance, the next figure shows a simple 3 x 3 mesh:
It consists in 9 cell centers, 12 internal faces and 12 external (boundary) faces. The numbers of the cell centers are shown in black and the number of the faces are shown in blue.
The non-zero coefficients for OpenFOAM would be:
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- | X | N | N | ||||||
| -2- | O | X | N | N | |||||
| -3- | O | X | N | ||||||
| -4- | O | X | N | N | |||||
| -5- | O | O | X | N | N | ||||
| -6- | O | O | X | N | |||||
| -7- | O | X | N | ||||||
| -8- | O | O | X | N | |||||
| -9- | O | O | X |
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- | 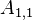 |
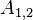 |
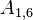 |
||||||
| -2- | 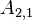 |
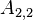 |
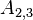 |
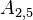 |
|||||
| -3- | 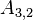 |
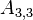 |
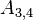 |
||||||
| -4- | 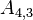 |
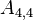 |
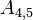 |
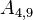
| |||||
| -5- | 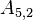 |
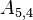 |
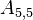 |
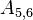 |
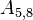 |
||||
| -6- | 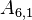 |
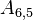 |
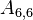 |
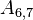 |
|||||
| -7- | 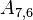 |
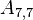 |
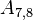 |
||||||
| -8- | 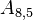 |
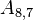 |
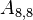 |
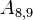
| |||||
| -9- | 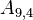 |
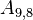 |
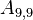
|
Some mathematical operations require distinguishing between the two coefficients as they are sometimes opposite in sign (for instance when fluxes are involved). OpenFOAM's mesh design anticipated this requirement, which is why every face has an owner cell and a neighbour cell. Owner, neighbour and diagonal coefficients are defined as:

Where:
- i is the matrix row number (corresponds to cell index); and
- j is the matrix column number (corresponds to cell index).
With this definition, the lower triangle has the owner coefficients; and the upper triangle has the neighbour coefficients. They are denoted:
- As discretization coefficients,
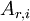 , where r indicates "related cells"[1];
, where r indicates "related cells"[1];
- As matrix coefficients:
- Owner coefficients are:
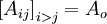 ; and
; and
- Neighbour coefficients are:
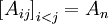 .
.
- Owner coefficients are:
With the above example the entries of the lowerPtr_, upperPtr_ and diagPtr_ array are:
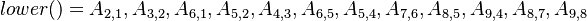
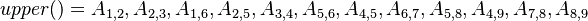
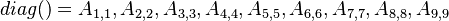
Note that the ordering of the entries of the arrays lowerPtr_ and upperPtr_ are stored according to the face number and of the array diagPtr_ according to the cell number.
With this consistently applied across the mesh, a direction for positive surface-normal vectors is defined: a positive surface-normal vector (such as fluxes) points away from the owner cell, and towards the neighbour cell.
2.3 lduAddressing
The lower, diagonal and upper coefficients are all scalarFields (basically a list), but they are indexed differently. The diagonal coefficients are indexed by cell index; whereas the upper and lower triangles are indexed by face index. In order to get the indices to match, an addressing array is provided for the lower and upper triangles to translate their face index into a corresponding cell index. This addressing array is called an lduAddressing array.
The lduAdressing class (see https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1lduAddressing.html) contains two function which return the label list containing the owner (lowerAddr()) and neighbor (upperAddr()) of each face. For our example above the two arrays look like:
lowerAddr() = 1, 2, 1, 2, 3, 5, 4, 6, 5, 4, 7, 8 upperAddr() = 2, 3, 6, 5, 4, 6, 5, 7, 8, 9, 8, 9
The above arrays are ordered according to the face number and contain the owner (lowerAddr()) and neighbor (upperAddr()) of the face.
2.3.1 When do you need it?
lduAddressing is needed anytime you need to perform an operation on all rows of an lduMatrix that involves both diagonal and off-diagonal coefficients.
2.4 How do you use it?
To use lduAddressing:
- separate operations involving the lower triangle from operations involving the upper triangle;
- loop over all the faces in the mesh;
- upper and lower triangle coefficients use the loop index - e.g. upper[facei] = ...
- diagonal coefficients use the lduAddressing coefficient of the face index:
- diag[l[facei]] -= lower[facei], where l is the lduAddressing for the lower triangle; and
- diag[u[facei]] -= upper[facei], where u is the lduAddressing for the upper triangle.
2.4.1 Example
For example, the negSumDiag operation is frequently required. This is where the diagonal is the negative sum of its neighbours:
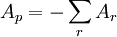
The guts of its code is:
for (register label face=0; face<l.size(); face++)
{
Diag[l[face]] -= Lower[face];
Diag[u[face]] -= Upper[face];
}
Where:
- Diag is the diagonal coefficient;
- l is the lduAddressing for the lower triangle;
- u is the lduAddressing for the upper triangle;
- Lower is the lower triangle; and
- Upper is the upper triangle.
2.5 Diagonal, symmetric, and asymmetric matrices
It is mandatory to define the diagonal; the others are not required. If only one of the lower or upper triangles are defined, the matrix is assumed to be symmetric. If both are defined, it will assume the matrix is asymmetric, even if they are equal.
| lowerPtr | diagPtr | upperPtr | Result |
|---|---|---|---|
| Yes/No | No | Yes/No | Invalid matrix - error thrown |
| No | Yes | No | Diagonal matrix |
| Yes | Yes | No | Symmetric matrix |
| No | Yes | Yes | Symmetric matrix |
| Yes | Yes | Yes | Asymmetric matrix |
- Caution: Accessing the opposite pointer without a const modifier will convert the matrix to an asymmetric matrix. To modify the off-diagonal of a symmetric matrix, first test which pointer is active using hasUpper() and hasLower().
2.6 OpenFOAM code example
For example, in calculating the diffusion of a quantity 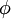 , the governing equation is:
, the governing equation is:

This is the Laplacian, which is calculated in the finite volume method using fvm::laplacian. The discretization coefficients are:
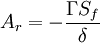
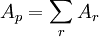
To implement this in OpenFOAM:
GeometricField<scalar, fvsPatchField, surfaceMesh> gammaMagSf ( gamma*mesh.magSf() ); fvMatrix<Type>& fvm; fvm.upper() = deltaCoeffs.internalField() * gamma*mesh.magSf().internalField(); fvm.negSumDiag();
- Note:
- fvm.lower is never mentioned - this is because it is equal to fvm.upper and a symmetric matrix is being created.
- fvm.upper is opposite in sign to
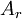 above - this is because fvm.lower are matrix coefficients, whereas
above - this is because fvm.lower are matrix coefficients, whereas 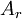 are discretization coefficients.
are discretization coefficients.
2.7 Examples how the matrix is build
2.7.1 Laplacian
In the following example we show how the coefficients for the matrix resulting from the discretization of the Laplacian equation are derived. Similar information can be found in the very good book of [2] which describes the details of the discretization in OpenFOAM.
The Laplacian equation reads:

Note the for the explanation here we assume a constant 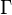 .
.
Being  the variable solved for and
the variable solved for and  the diffusivity.
the diffusivity.
The above equation is integrated over the control volume and together with the Gauss theorem we get
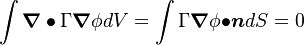
Substituting the integral over the surface of the volume with a summation over the cell faces we get:

The the scalar product of the gradient of  with the face Area vector
with the face Area vector  is discretized as follows:
is discretized as follows:
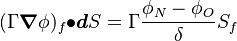
The face normal vector in OpenFoam is pointing from the face owner (the cell with the lower index) to the face neighbor (the cell with the higher index). This means that if the value 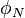 is higher than
is higher than 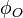 the scalar product
the scalar product 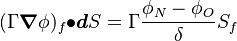 is positive and vice versa.
is positive and vice versa.
Finally we get:
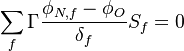
Were 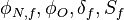 are the variable stored at the face neighbor cell center, the variable stored at the owner cell center, the distance from the owner cell center to the neighbor cell center and the face are, respectively. Finally we get for the matrix coefficients for the case where the value of
are the variable stored at the face neighbor cell center, the variable stored at the owner cell center, the distance from the owner cell center to the neighbor cell center and the face are, respectively. Finally we get for the matrix coefficients for the case where the value of  at the boundary is specified:
at the boundary is specified:
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- | 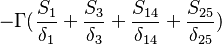 |
 |
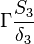 |
||||||
| -2- |  |
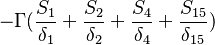 |
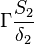 |
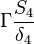 |
|||||
| -3- | 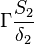 |
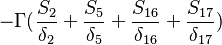 |
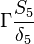 |
||||||
| -4- | 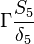 |
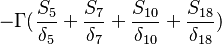 |
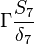 |
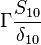
| |||||
| -5- | 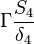 |
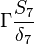 |
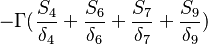 |
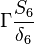 |
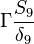 |
||||
| -6- | 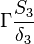 |
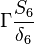 |
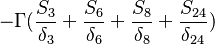 |
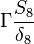 |
|||||
| -7- | 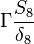 |
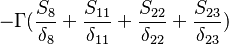 |
 |
||||||
| -8- | 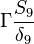 |
 |
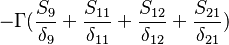 |
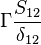
| |||||
| -9- | 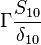 |
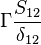 |
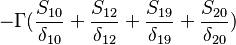
|
The source vector resulting from the fixed value boundary condition will look like:
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- | 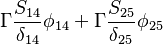 |
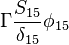 |
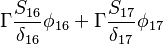 |
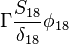 |
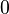 |
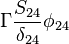 |
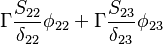 |
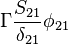 |
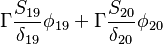
|
For a constant gradient 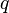 boundary conditions the matrix looks like:
boundary conditions the matrix looks like:
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- | 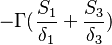 |
 |
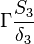 |
||||||
| -2- |  |
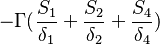 |
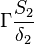 |
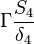 |
|||||
| -3- | 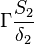 |
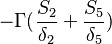 |
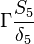 |
||||||
| -4- | 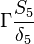 |
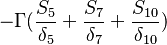 |
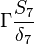 |
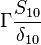
| |||||
| -5- | 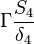 |
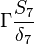 |
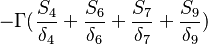 |
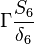 |
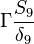 |
||||
| -6- | 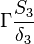 |
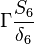 |
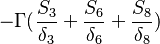 |
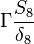 |
|||||
| -7- | 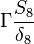 |
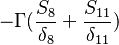 |
 |
||||||
| -8- | 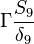 |
 |
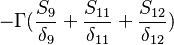 |
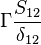
| |||||
| -9- | 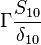 |
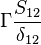 |
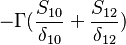
|
The source vector resulting from the fixed gradient boundary condition will look like:
| i | -1- | -2- | -3- | -4- | -5- | -6- | -7- | -8- | -9- |
|---|---|---|---|---|---|---|---|---|---|
| -1- |  |
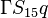 |
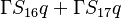 |
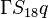 |
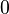 |
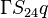 |
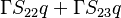 |
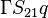 |
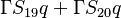
|
template<class Type, class GType> tmp<fvMatrix<Type>> gaussLaplacianScheme<Type, GType>::fvmLaplacian ( const GeometricField<GType, fvsPatchField, surfaceMesh>& gamma, const GeometricField<Type, fvPatchField, volMesh>& vf ) { const fvMesh& mesh = this->mesh(); const surfaceVectorField Sn(mesh.Sf()/mesh.magSf()); const surfaceVectorField SfGamma(mesh.Sf() & gamma); const GeometricField<scalar, fvsPatchField, surfaceMesh> SfGammaSn ( SfGamma & Sn ); const surfaceVectorField SfGammaCorr(SfGamma - SfGammaSn*Sn); tmp<fvMatrix<Type>> tfvm = fvmLaplacianUncorrected ( SfGammaSn, this->tsnGradScheme_().deltaCoeffs(vf), vf ); fvMatrix<Type>& fvm = tfvm.ref(); tmp<GeometricField<Type, fvsPatchField, surfaceMesh>> tfaceFluxCorrection = gammaSnGradCorr(SfGammaCorr, vf); if (this->tsnGradScheme_().corrected()) { tfaceFluxCorrection.ref() += SfGammaSn*this->tsnGradScheme_().correction(vf); } fvm.source() -= mesh.V()*fvc::div(tfaceFluxCorrection())().primitiveField(); if (mesh.fluxRequired(vf.name())) { fvm.faceFluxCorrectionPtr() = tfaceFluxCorrection.ptr(); } return tfvm; } template<class Type, class GType> tmp<fvMatrix<Type>> gaussLaplacianScheme<Type, GType>::fvmLaplacianUncorrected ( const surfaceScalarField& gammaMagSf, const surfaceScalarField& deltaCoeffs, const GeometricField<Type, fvPatchField, volMesh>& vf ) { tmp<fvMatrix<Type>> tfvm ( new fvMatrix<Type> ( vf, deltaCoeffs.dimensions()*gammaMagSf.dimensions()*vf.dimensions() ) ); fvMatrix<Type>& fvm = tfvm.ref(); fvm.upper() = deltaCoeffs.primitiveField()*gammaMagSf.primitiveField(); fvm.negSumDiag(); forAll(vf.boundaryField(), patchi) { const fvPatchField<Type>& pvf = vf.boundaryField()[patchi]; const fvsPatchScalarField& pGamma = gammaMagSf.boundaryField()[patchi]; const fvsPatchScalarField& pDeltaCoeffs = deltaCoeffs.boundaryField()[patchi]; if (pvf.coupled()) { fvm.internalCoeffs()[patchi] = pGamma*pvf.gradientInternalCoeffs(pDeltaCoeffs); fvm.boundaryCoeffs()[patchi] = -pGamma*pvf.gradientBoundaryCoeffs(pDeltaCoeffs); } else { fvm.internalCoeffs()[patchi] = pGamma*pvf.gradientInternalCoeffs(); fvm.boundaryCoeffs()[patchi] = -pGamma*pvf.gradientBoundaryCoeffs(); } } return tfvm; }
template<class Type> Foam::tmp<Foam::Field<Type>> Foam::fixedValueFvPatchField<Type>::gradientInternalCoeffs() const { return -pTraits<Type>::one*this->patch().deltaCoeffs(); } template<class Type> Foam::tmp<Foam::Field<Type>> Foam::fixedValueFvPatchField<Type>::gradientBoundaryCoeffs() const { return this->patch().deltaCoeffs()*(*this); }
template<class Type> Foam::tmp<Foam::Field<Type>> Foam::fixedGradientFvPatchField<Type>::gradientInternalCoeffs() const { return tmp<Field<Type>>::New(this->size(), Zero); } template<class Type> Foam::tmp<Foam::Field<Type>> Foam::fixedGradientFvPatchField<Type>::gradientBoundaryCoeffs() const { return gradient(); }
2.7.2 Divergence
3 fvMatrix
Since OpenFOAM implements multiple numerical strategies such as finite difference, finite area, finite element, and so on, everything that is specific to any one of these strategies is stripped out of the base class lduMatrix. This facilitates code reuse.
fvMatrix is the finite volume extension of lduMatrix. It includes the source, B, as well as a reference to the field, 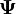 from
from 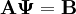 . It handles what happens on the boundaries, and also implements specific operations that occur frequently in finite volume algorithms, such as fvMatrix;;H.
. It handles what happens on the boundaries, and also implements specific operations that occur frequently in finite volume algorithms, such as fvMatrix;;H.
4 Notes
- ↑ What I'm calling related cells is conventionally called neighbours. But OpenFOAM has a different meaning for neighbours, so the term related cells is used.
- ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):