Difference between revisions of "Contrib/CompressibleMixingPhaseChangeFoam"

Revision as of 15:31, 6 August 2013

Solver for two fluids with phase change (for example - water <---> steam), pressure and temperature density dependence

1 Model Equations Derivation

Equation of state

Low-compressible fluid: 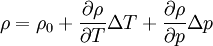$\rho = \rho_0 + \frac{\partial \rho}{\partial T} \Delta T + \frac{\partial \rho}{\partial p} \Delta p$

Ideal gas: 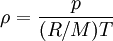$\rho=\frac{p}{(R/M)T}$

By combining this equations, we can get general relation:

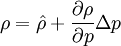
$\rho = \hat \rho + \frac{\partial \rho}{\partial p} \Delta p$

where 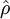$\hat \rho$ computed with respect to previous formulations

mixture density 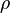$\rho$ calculated as

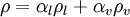
$\rho = \alpha_l \rho_l + \alpha_v \rho_v$

Here, and afterthere indices:

1,l,f - for liquid (heavy media with low compressibility)

2,g,s - for gas (light media (like steam) with big compressibility)

without index - mixture variable (or all variables local to some phase)

Liquid volume transport

Let us consider transport of liquid (heavy phase) volume fraction 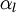$\alpha_l$ :

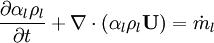
$\frac{\partial \alpha_l \rho_l}{\partial t} + \nabla \cdot \left ( \alpha_l \rho_l \mathbf{U} \right ) = \dot m_l$

By converting to volume fluxes we get:

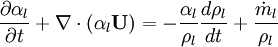
$\frac {\partial \alpha_l}{\partial t} + \nabla \cdot \left ( \alpha_l \textbf{U} \right ) = -\frac {\alpha_l}{\rho_l} \frac {d \rho_l}{dt} + \frac {\dot m_l}{\rho_l}$

Using equation of state, we can reformulate substantial derivative for density in terms of pressure for any phase:

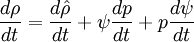
$\frac {d \rho}{dt}= \frac {d \hat \rho} {dt} + \psi \frac {dp} {dt} + p \frac {d \psi}{dt}$

General rule for converting from mass to volume fluxes in transport equation

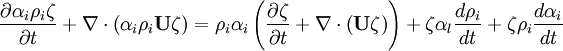
$\frac{\partial \alpha_i \rho_i \zeta}{\partial t} + \nabla \cdot \left ( \alpha_i \rho_i \textbf{U} \zeta \right ) = \rho_i \alpha_i \left ( \frac {\partial \zeta}{\partial t} + \nabla \cdot \left ( \textbf{U} \zeta \right ) \right ) + \zeta \alpha_l \frac {d \rho_i}{dt} + \zeta \rho_i \frac {d \alpha_i}{dt}$

Momentum equation (velocity prediction)

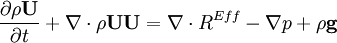
$\frac {\partial \rho \textbf{U}}{\partial t} + \nabla \cdot \rho \textbf{U} \textbf{U} = \nabla \cdot R^{Eff} - \nabla p + \rho \textbf{g}$

by substituting piezometric pressure 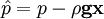$\hat p = p - \rho \textbf{g} \textbf{x}$ we get:

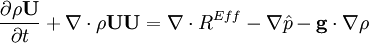
$\frac {\partial \rho \textbf{U}}{\partial t} + \nabla \cdot \rho \textbf{U} \textbf{U} = \nabla \cdot R^{Eff} - \nabla \hat p - \textbf{g} \cdot \nabla \rho$

Pressure equation obtained by summation of equation for volume phase fraction of liquid and gas phases:

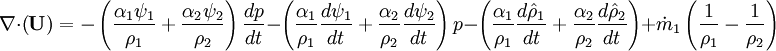
$\nabla \cdot \left ( \textbf{U} \right ) = - \left ( \frac {\alpha_1 \psi_1}{\rho_1} + \frac {\alpha_2 \psi_2}{\rho_2} \right ) \frac {d p}{d t} - \left ( \frac {\alpha_1}{\rho_1} \frac {d \psi_1}{d t} + \frac {\alpha_2}{\rho_2} \frac {d \psi_2}{d t} \right ) p - \left ( \frac {\alpha_1}{\rho_1} \frac {d \hat \rho_1}{d t} + \frac {\alpha_2}{\rho_2} \frac {d \hat \rho_2}{d t} \right )+ \dot m_1 \left ( \frac{1}{\rho_1} - \frac{1}{\rho_2} \right )$

Energy equation

Energy equation for mixture temperature obtained from sum of energy equations for each phase. Consider internal energy equation for phase-1:

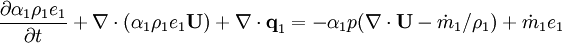
$\frac{\partial \alpha_1 \rho_1 e_1} {\partial t} + \nabla \cdot \left ( \alpha_1 \rho_1 e_1 \textbf{U} \right ) + \nabla \cdot \textbf{q}_1 = -\alpha_1 p (\nabla \cdot \textbf{U} - \dot m_1 / \rho_1) + \dot m_1 e_1$

By combining equations of phases, we get internal energy balance for mixture in temperatures:

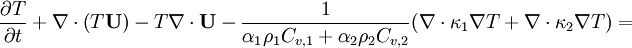
$\frac{\partial T}{\partial t} + \nabla \cdot \left ( T \textbf{U} \right ) - T \nabla \cdot \textbf{U} -\frac{1}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}} (\nabla \cdot \kappa_1 \nabla T + \nabla \cdot \kappa_2 \nabla T) =$

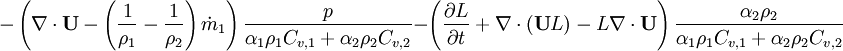
$-\left ( \nabla \cdot \textbf{U} - \left(\frac{1}{\rho_1}-\frac{1}{\rho_2}\right) \dot m_1 \right ) \frac{p}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}} - \left ( \frac{\partial L}{\partial t} + \nabla \cdot (\textbf{U} L) - L \nabla \cdot \textbf{U} \right ) \frac{\alpha_2 \rho_2}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}}$

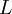Where $L$ - latent heat of evaporation

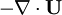Linking liquid volume transport to pressure equation is done by introducing $+\alpha_1 \nabla \cdot \textbf{U}$ and $-\alpha_1 \nabla \cdot \textbf{U}$ at r.h.s of volume fraction balance equation. Then, $-\nabla \cdot \textbf{U}$ replaced by value from pressure equation

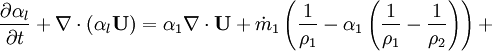
$\frac {\partial \alpha_l}{\partial t} + \nabla \cdot \left ( \alpha_l \textbf{U} \right ) = \alpha_1 \nabla \cdot \textbf{U} + \dot m_1 \left (\frac{1}{\rho_1} - \alpha_1 \left (\frac{1}{\rho_1} - \frac{1}{\rho_2} \right ) \right ) +$

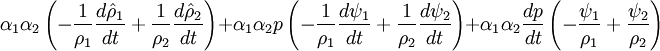
$\alpha_1 \alpha_2 \left ( -\frac{1}{\rho_1} \frac{d \hat \rho_1}{d t} + \frac{1}{\rho_2} \frac{d \hat \rho_2}{d t}\right ) +\alpha_1 \alpha_2 p \left ( -\frac{1}{\rho_1} \frac{d \psi_1}{d t} + \frac{1}{\rho_2} \frac{d \psi_2}{d t}\right ) +\alpha_1 \alpha_2 \frac{d p}{d t}\left ( -\frac{\psi_1}{\rho_1} + \frac{\psi_2}{\rho_2} \right )$

Phase change model

Schnerr-Sauer

2 Model Equations Summary

3 Tutorial cases

Case #1 - Water Evaporation in Cavity

Solver sources and tutorials located here

@@ Line 107: / Line 107: @@
 * '''Energy equation'''
-Energy equation for mixture temperature obtained from sum of energy equations for each phase. Consider energy equation for phase-1:
+Energy equation for mixture temperature obtained from sum of energy equations for each phase. Consider internal energy equation for phase-1:
 <math>
@@ Line 113: / Line 113: @@
 \nabla \cdot \left ( \alpha_1 \rho_1 e_1 \textbf{U} \right ) + \nabla \cdot \textbf{q}_1
 =
--\alpha_1 p \nabla \cdot \textbf{U}
+-\alpha_1 p (\nabla \cdot \textbf{U} - \dot m_1 / \rho_1)
 +
 \dot m_1 e_1
 </math>
-by converting to enthalpies we get:
-<math>
+By combining equations of phases, we get internal energy balance for mixture in temperatures:
-\frac{\partial \alpha_1 \rho_1 h_1} {\partial t} +
-\nabla \cdot \left ( \alpha_1 \rho_1 h_1 \textbf{U} \right )-
-\left (
-\frac {\partial \alpha_1 p}{\partial t} + \nabla \cdot \left ( \alpha_1 p \textbf{U} \right )
-\right )
-+ \nabla \cdot \textbf{q}_1
-=
--\alpha_1 p \nabla \cdot \textbf{U}+
-\dot m_1 h_1 - \dot m_1 \frac{p}{\rho_1}
-</math>
-By substituting temperature instead of enthalpy, after conversion to volume fluxes we get equation for temperature (divided by
-<math>\rho_1 C_{p,1} </math> )
-<math>
-\alpha_1 \left (\frac{\partial T}{\partial t} + \nabla \cdot \left ( T \textbf{U} \right ) \right )
-+ T \frac{\alpha_1}{\rho_1} \frac{d \rho_1}{d t} + T \frac{d \alpha_1}{d t} - \frac{1}{\rho_1 C_{p,1}} \nabla \cdot \textbf{q}_1
-=
-T \frac{\dot m_1}{\rho_1} - \frac{1}{\rho_1 C_{p,1}} \frac{p}{\rho_1} \dot m_1 +
-\frac{1}{\rho_1 C_{p,1}}
-\left (
-\alpha_1 \frac {d p}{d t} + p \frac {d \alpha_1}{d t}
-\right )
-</math>
-By combining equations of phases, we get energy balance for mixture:
 <math>
 \frac{\partial T}{\partial t} + \nabla \cdot \left ( T \textbf{U} \right ) - T \nabla \cdot \textbf{U}
--\frac{1}{\rho_1 C_{p,1}} \nabla \cdot \kappa_1 \nabla T -\frac{1}{\rho_2 C_{p,2}} \nabla \cdot \kappa_2 \nabla T
+-\frac{1}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}} (\nabla \cdot \kappa_1 \nabla T + \nabla \cdot \kappa_2 \nabla T)
 =
 </math>
 <math>
-\left ( \frac{\alpha_1}{\rho_1 C_{p,1}} + \frac{\alpha_2}{\rho_2 C_{p,2}} \right ) \frac{d p}{d t}
+-\left ( \nabla \cdot \textbf{U} - \left(\frac{1}{\rho_1}-\frac{1}{\rho_2}\right) \dot m_1 \right )
-+ \frac{p}{\rho_1 C_{p,1}}\frac{d \alpha_1}{d t} + \frac{p}{\rho_2 C_{p,2}}\frac{d \alpha_2}{d t}
+\frac{p}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}}
-+ \dot m_1 p \left (-\frac{1}{\rho_1 \rho_1 C_{p,1}} + \frac{1}{\rho_2 \rho_2 C_{p,2}}\right )
+- \left ( \frac{\partial L}{\partial t} + \nabla \cdot (\textbf{U} L) - L \nabla \cdot \textbf{U} \right )
+\frac{\alpha_2 \rho_2}{\alpha_1 \rho_1 C_{v,1} + \alpha_2 \rho_2 C_{v,2}}
 </math>
+Where <math> L </math> - latent heat of evaporation
 * '''Linking liquid volume transport to pressure equation''' is done by introducing <math>+\alpha_1 \nabla \cdot \textbf{U}</math> and <math>-\alpha_1 \nabla \cdot \textbf{U}</math> at r.h.s of volume fraction balance equation. Then, <math>-\nabla \cdot \textbf{U}</math> replaced by value from pressure equation
@@ Line 179: / Line 155: @@
 * Phase change model
+ Schnerr-Sauer
 == Model Equations Summary ==