Difference between revisions of "FireFoam"
(→Evolution of Mass) |
(→Evolution of Mass) |
||
| Line 181: | Line 181: | ||
<math> Sh</math>, <math> Sc </math>, <math> \tau_{p,k} = \rho_{p,k} d_p^2 / (18 \mu) </math> and <math> H_M </math> are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. <math> \rho_p,k </math> is the particle density and <math> \mu </math> the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number). | <math> Sh</math>, <math> Sc </math>, <math> \tau_{p,k} = \rho_{p,k} d_p^2 / (18 \mu) </math> and <math> H_M </math> are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. <math> \rho_p,k </math> is the particle density and <math> \mu </math> the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number). | ||
| + | |||
| + | |||
| + | The source therm in the pressure and in the species equations of the carrier phase are calculated in intermediate/clouds/Templates/ReactingCloud/ReactingCloudI.H: | ||
| + | |||
| + | |||
| + | |||
| + | <br><cpp> | ||
| + | |||
| + | template<class CloudType> | ||
| + | inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> | ||
| + | Foam::ReactingCloud<CloudType>::Srho(const label i) const | ||
| + | { | ||
| + | tmp<volScalarField::Internal> tRhoi | ||
| + | ( | ||
| + | new volScalarField::Internal | ||
| + | ( | ||
| + | IOobject | ||
| + | ( | ||
| + | this->name() + ":rhoTrans", | ||
| + | this->db().time().timeName(), | ||
| + | this->db(), | ||
| + | IOobject::NO_READ, | ||
| + | IOobject::NO_WRITE, | ||
| + | false | ||
| + | ), | ||
| + | this->mesh(), | ||
| + | dimensionedScalar | ||
| + | ( | ||
| + | rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero | ||
| + | ) | ||
| + | ) | ||
| + | ); | ||
| + | |||
| + | if (this->solution().coupled()) | ||
| + | { | ||
| + | scalarField& rhoi = tRhoi.ref(); | ||
| + | rhoi = rhoTrans_[i]/(this->db().time().deltaTValue()*this->mesh().V()); | ||
| + | } | ||
| + | |||
| + | return tRhoi; | ||
| + | } | ||
| + | |||
| + | |||
| + | template<class CloudType> | ||
| + | inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> | ||
| + | Foam::ReactingCloud<CloudType>::Srho() const | ||
| + | { | ||
| + | tmp<volScalarField::Internal> trhoTrans | ||
| + | ( | ||
| + | new volScalarField::Internal | ||
| + | ( | ||
| + | IOobject | ||
| + | ( | ||
| + | this->name() + ":rhoTrans", | ||
| + | this->db().time().timeName(), | ||
| + | this->db(), | ||
| + | IOobject::NO_READ, | ||
| + | IOobject::NO_WRITE, | ||
| + | false | ||
| + | ), | ||
| + | this->mesh(), | ||
| + | dimensionedScalar | ||
| + | ( | ||
| + | rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero | ||
| + | ) | ||
| + | ) | ||
| + | ); | ||
| + | |||
| + | if (this->solution().coupled()) | ||
| + | { | ||
| + | scalarField& sourceField = trhoTrans.ref(); | ||
| + | forAll(rhoTrans_, i) | ||
| + | { | ||
| + | sourceField += rhoTrans_[i]; | ||
| + | } | ||
| + | |||
| + | sourceField /= this->db().time().deltaTValue()*this->mesh().V(); | ||
| + | } | ||
| + | |||
| + | return trhoTrans; | ||
| + | } | ||
| + | </cpp><br> | ||
====Evolution of Momentum==== | ====Evolution of Momentum==== | ||
Revision as of 17:58, 5 May 2019
fireFoam
Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling.
Contents
1 Solution Strategy
The source code can be found in fireFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | Copyright (C) 2011-2017 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application fireFoam Group grpCombustionSolvers Description Transient solver for fires and turbulent diffusion flames with reacting particle clouds, surface film and pyrolysis modelling. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "turbulentFluidThermoModel.H" #include "basicReactingCloud.H" #include "surfaceFilmModel.H" #include "pyrolysisModelCollection.H" #include "radiationModel.H" #include "SLGThermo.H" #include "solidChemistryModel.H" #include "psiReactionThermo.H" #include "CombustionModel.H" #include "pimpleControl.H" #include "fvOptions.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Transient solver for fires and turbulent diffusion flames" " with reacting particle clouds, surface film and pyrolysis modelling." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" #include "createTimeControls.H" #include "compressibleCourantNo.H" #include "setInitialDeltaT.H" #include "createRegionControls.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (runTime.run()) { #include "readTimeControls.H" #include "compressibleCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setMultiRegionDeltaT.H" #include "setDeltaT.H" ++runTime; Info<< "Time = " << runTime.timeName() << nl << endl; parcels.evolve(); surfaceFilm.evolve(); if(solvePyrolysisRegion) { pyrolysis.evolve(); } if (solvePrimaryRegion) { #include "rhoEqn.H" // --- PIMPLE loop while (pimple.loop()) { #include "UEqn.H" #include "YEEqn.H" // --- Pressure corrector loop while (pimple.correct()) { #include "pEqn.H" } if (pimple.turbCorr()) { turbulence->correct(); } } rho = thermo.rho(); } runTime.write(); runTime.printExecutionTime(Info); } Info<< "End" << endl; return 0; } // ************************************************************************* //
2 Equations
2.1 Equations Parcels
The particles in fireFoam are treated in a Lagrangian frame of reference. This means that each particle (or parcel which is an ensemble of a number of particles with the same properties) is tracked individually throughout the computational domain. For each parcel a ordinary differential equation is solved which describes the evolution of its mass, velocity (after one integration more also the position in space) and its temperature. The evolution of the particle mass is required besides for its own momentum equation to calculate the mass source term in the spices and the pressure equation of the carrier phase. The particle momentum equation through which the particle velocity and after one integration also the particle position is obtained, is required to calculate the forces acting from the particles on the carrier phase required in the momentum equation of the fluid. The energy equation of the particles (the temperature is obtained by an equation of state) is required to compute the source term due to the particles in the energy equation of the carrier phase. Note that some additional informations can be also found in https://www.politesi.polimi.it/bitstream/10589/134603/7/2017_07_Ghasemi.pdf and http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2013/EmilLjungskog/reactingParcelFilmFoam_report.pdf.
2.1.1 Evolution of Mass
According to [1] (see also https://trs.jpl.nasa.gov/bitstream/handle/2014/22473/97-0966.pdf?sequence=1)
the evaporating mass of a spherical droplet with the diameter 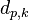 and mass
and mass 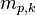 (the subscript k denotes the spices k since in OpenFOAM different spices can be tracked) can be expressed in the following form:
(the subscript k denotes the spices k since in OpenFOAM different spices can be tracked) can be expressed in the following form:
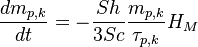 | (x) |
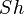 ,
, 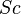 ,
, 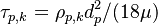 and
and 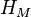 are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively.
are the Sherwood number, the Schmidt number, the particle relaxation time and the potential driving the evaporation, respectively. 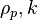 is the particle density and
is the particle density and 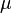 the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number).
the dynamic viscosity of the carrier phase. The Sherwood number describes the ratio between the convective mass transfer and the diffusion (https://en.wikipedia.org/wiki/Sherwood_number). The Schmidt number is defined as the ratio between viscous diffusion rate and mass diffusion rate (https://en.wikipedia.org/wiki/Schmidt_number).
The source therm in the pressure and in the species equations of the carrier phase are calculated in intermediate/clouds/Templates/ReactingCloud/ReactingCloudI.H:
template<class CloudType> inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> Foam::ReactingCloud<CloudType>::Srho(const label i) const { tmp<volScalarField::Internal> tRhoi ( new volScalarField::Internal ( IOobject ( this->name() + ":rhoTrans", this->db().time().timeName(), this->db(), IOobject::NO_READ, IOobject::NO_WRITE, false ), this->mesh(), dimensionedScalar ( rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero ) ) ); if (this->solution().coupled()) { scalarField& rhoi = tRhoi.ref(); rhoi = rhoTrans_[i]/(this->db().time().deltaTValue()*this->mesh().V()); } return tRhoi; } template<class CloudType> inline Foam::tmp<Foam::DimensionedField<Foam::scalar, Foam::volMesh>> Foam::ReactingCloud<CloudType>::Srho() const { tmp<volScalarField::Internal> trhoTrans ( new volScalarField::Internal ( IOobject ( this->name() + ":rhoTrans", this->db().time().timeName(), this->db(), IOobject::NO_READ, IOobject::NO_WRITE, false ), this->mesh(), dimensionedScalar ( rhoTrans_[0].dimensions()/dimTime/dimVolume, Zero ) ) ); if (this->solution().coupled()) { scalarField& sourceField = trhoTrans.ref(); forAll(rhoTrans_, i) { sourceField += rhoTrans_[i]; } sourceField /= this->db().time().deltaTValue()*this->mesh().V(); } return trhoTrans; }
2.1.2 Evolution of Momentum
2.1.3 Evolution of Energy
2.2 Equations Liquid Film
The equation describing the evolution of the liquid film can be found in http://www.ilasseurope.org/ICLASS/iclass2012_Heidelberg/Contributions/Paper-pdfs/Contribution1294_b.pdf and https://www.witpress.com/Secure/elibrary/papers/MPF11/MPF11020FU1.pdf. A description of the method used to derive the equation can be found in https://www.researchgate.net/profile/Petr_Vita/publication/313655371_Thin_Film_Fluid_Flow_Simulation_on_Rotating_Discs/links/58a1a592a6fdccf5e9707665/Thin-Film-Fluid-Flow-Simulation-on-Rotating-Discs.pdf.
2.2.1 Mass Conservation Film
The conservation of mass reads:
 | (1) |
 represents the mean film velocity,
represents the mean film velocity, 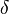 the film height and
the film height and 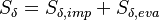 the mass source term resulting
from the impingement of the liquid droplets on the film surface
the mass source term resulting
from the impingement of the liquid droplets on the film surface 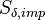 and due to the evaporation of the film
and due to the evaporation of the film 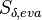 . Note
that the source term due to evaporation
. Note
that the source term due to evaporation 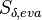 will be inserted into the pressure equation for the gas phase and also into the equation for the spices
transport.
The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
will be inserted into the pressure equation for the gas phase and also into the equation for the spices
transport.
The source code of the continuity equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveContinuity() { if (debug) { InfoInFunction << endl; } solve ( fvm::ddt(deltaRho_) + fvc::div(phi_) == - rhoSp_ ); }
2.2.2 Momentum Conservation Film
The momentum conservation reads:
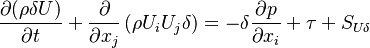 | (2) |
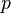 represents the pressure,
represents the pressure, 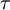 the stress like components of the forces acting on the filme and
the stress like components of the forces acting on the filme and 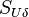 represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects
represents the contribution to the momentum by the impinging droplets. The pressure contribution is divided in three components: The contribution due to capillary effects 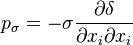 , the hydrostatic contribution
, the hydrostatic contribution 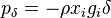 and the contribution of the pressure originated by the surrounding gas
and the contribution of the pressure originated by the surrounding gas 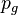 .
. 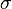 represents the surface tension. The stress like contribution is divided in the wall shear stress
represents the surface tension. The stress like contribution is divided in the wall shear stress 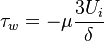 , the gravity force tangential to the wall
, the gravity force tangential to the wall 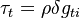 and the contribution of the contact line force
and the contribution of the contact line force 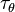 .
. 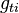 is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
is the component of the gravity parallel to the wall. Finally the momentum equation can be written as:
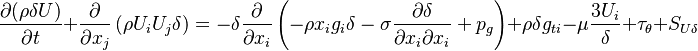 | (3) |
The source code of the momentum equation can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
tmp<Foam::fvVectorMatrix> kinematicSingleLayer::solveMomentum ( const volScalarField& pu, const volScalarField& pp ) { if (debug) { InfoInFunction << endl; } // Momentum tmp<fvVectorMatrix> tUEqn ( fvm::ddt(deltaRho_, U_) + fvm::div(phi_, U_) == - USp_ // - fvm::SuSp(rhoSp_, U_) - rhoSp_*U_ + forces_.correct(U_) + turbulence_->Su(U_) ); fvVectorMatrix& UEqn = tUEqn.ref(); UEqn.relax(); if (momentumPredictor_) { solve ( UEqn == fvc::reconstruct ( - fvc::interpolate(delta_) * ( regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) + fvc::snGrad(delta_)*fvc::interpolate(pp) ) - fvc::flux(rho_*gTan()) ) ) ); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); } return tUEqn; }
2.2.3 Energy Conservation Film
The energy equation reads:
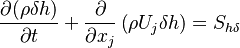 | (4) |
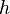 represents the mean film enthalpy and
represents the mean film enthalpy and 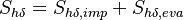 represents the contribution of the impinging droplets
represents the contribution of the impinging droplets 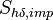 and the evaporation of the film
and the evaporation of the film 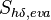 to the
energy equation. Note that the energy required by the film (or a portion of it) to evaporate
to the
energy equation. Note that the energy required by the film (or a portion of it) to evaporate 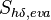 is cast as source term into the energy equation of the surrounding gas. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
is cast as source term into the energy equation of the surrounding gas. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer:
void thermoSingleLayer::solveEnergy() { if (debug) { InfoInFunction << endl; } dimensionedScalar residualDeltaRho ( "residualDeltaRho", deltaRho_.dimensions(), 1e-10 ); solve ( fvm::ddt(deltaRho_, hs_) + fvm::div(phi_, hs_) == - hsSp_ + q(hs_) + radiation_->Shs() ); correctThermoFields(); // Evaluate viscosity from user-model viscosity_->correct(pPrimary_, T_); // Update film wall and surface temperatures updateSurfaceTemperatures(); }
2.2.4 Film Thickness Equation
The last equation missing is the linear equation used to get the film thickness 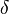 . In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P
. In order to get a tighter coupling between the momentum equation and the continuity equation, the same strategy used to get a coupling between momentum and continuity equation in pressure based solvers (see https://openfoamwiki.net/index.php/ChtMultiRegionFoam and https://openfoamwiki.net/index.php/SimpleFoam and references therein ) is used: The discrete momentum equation is used to get a relation for
the velocity at point P 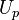 which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
which is then inserted into the continuity equation (1). The most convenient way to illustrate the procedure, is to write down the momentum equation in its discrete form:
![\rho \bold {U_p} \delta = \rho \left [ \bold { H[U] } \bold {\frac {1}{A_P}} - \bold {\frac {1}{A_P}}\delta \nabla \left ( \underbrace{-\rho g_i x_i}_{P_p} \delta - \underbrace{\sigma \nabla \nabla \delta + p_g}_{P_u} \right ) + \bold {\frac {1}{A_P}}\rho \delta g_t \right ] \delta](/images/math/1/4/4/1449081c4710027a4a917a67b76e63d8.png) | (5) |
The operator ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the
contained the contribution of the of the neighbouring velocities and the source term to the velocity at cell centre P. The explicit and implicite source terms included into the ![\bold H[U]](/images/math/a/6/5/a6568548bfa99b87e4cb0a03afad872b.png) are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
are the contributions due to the viscose shear, the influence of the contact angle and the contribution of the
particle impingement. In order that equation (5) can be inserted into the continuity equation the divergence has to be taken:
![\rho \nabla \cdot \left ( \bold {U_p} \delta \right ) =
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \bold {\frac {\delta}{A_P}} \nabla \left ( {P_p} \delta +{P_u} \right ) + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right )](/images/math/d/0/1/d01b1ab158ed586aad40b8a661609dd0.png) | (6) |
The above equation can be inserted into the continuity equation to obtain:
![\frac{ \partial (\rho \delta )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {\delta^2}{A_P} \nabla {P_p} - \frac {\delta P_p}{A_P} \nabla {\delta} - \bold {\frac {\delta}{A_P}} \nabla {P_u} + {\frac {\delta}{\bold A_P}}\rho g_t \right ] \delta \right ) = S_{\delta}](/images/math/a/7/5/a75cca6b4eadbbd675d0306542636176.png) | (7) |
It is obvious that the above equation is non linear in 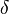 . In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
. In order to be solved it has to be linearised and an iterative method has be applied to obtain an
approximate solution.
In order to obtain the final set of equations which are solved in this solver, a Picard or fixed point iteration is used (see e.g. https://hplgit.github.io/num-methods-for-PDEs/doc/pub/nonlin/pdf/nonlin-4print.pdf or http://web.engr.uky.edu/~acfd/me690-lctr-nts.pdf):
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k P_p}{A_P} \nabla {\delta^{k+1}} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) = S_{\delta}](/images/math/5/4/f/54f1c220c3827744789ebcd9820f8f4b.png) | (8) |
The superscript k denote the solution computed at the last iteration an the superscript k+1 denotes the solution of the current iteration which has to be computed by solving the linear system resulting from the discretization. After separating the linear and the still non linear terms of the above equation we obtain:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k+1} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/8/2/3/823a63f544781d33fd0bacc9b5ba0531.png) | (9) |
Since the above equation still contains a non linear contribution it has remaining 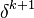 has to be approximated by the value at the previous iteration step
has to be approximated by the value at the previous iteration step
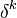 :
:
![\frac{ \partial (\rho \delta^{k+1} )}{\partial t} +
\rho \nabla \cdot \left ( \left [ \bold {\frac { \bold { H[U] }}{A_P}} - \frac {{\delta^k}^2}{A_P} \nabla {P_p} - \frac {\delta^k}{\bold A_P} \nabla {P_u} + {\frac {\delta^k}{\bold A_P}}\rho g_t \right ] \delta^{k+1} \right ) - \nabla \cdot \left ( \frac {\delta^k\delta^{k} P_p}{A_P} \nabla {\delta^{k+1}} \right ) = S_{\delta}](/images/math/f/c/b/fcb9c168d16e87fc3f62d76c091541b5.png) | (10) |
which is the final form solved in the present solver. The source code can be found in src/regionModels/surfaceFilmModels/kinematicSingleLayer:
void kinematicSingleLayer::solveThickness ( const volScalarField& pu, const volScalarField& pp, const fvVectorMatrix& UEqn ) { if (debug) { InfoInFunction << endl; } volScalarField rUA(1.0/UEqn.A()); U_ = rUA*UEqn.H(); surfaceScalarField deltarUAf(fvc::interpolate(delta_*rUA)); surfaceScalarField rhof(fvc::interpolate(rho_)); surfaceScalarField phiAdd ( "phiAdd", regionMesh().magSf() * ( fvc::snGrad(pu, "snGrad(p)") + fvc::snGrad(pp, "snGrad(p)")*fvc::interpolate(delta_) ) - fvc::flux(rho_*gTan()) ); constrainFilmField(phiAdd, 0.0); surfaceScalarField phid ( "phid", fvc::flux(U_*rho_) - deltarUAf*phiAdd*rhof ); constrainFilmField(phid, 0.0); surfaceScalarField ddrhorUAppf ( "deltaCoeff", fvc::interpolate(delta_)*deltarUAf*rhof*fvc::interpolate(pp) ); regionMesh().setFluxRequired(delta_.name()); for (int nonOrth=0; nonOrth<=nNonOrthCorr_; nonOrth++) { // Film thickness equation fvScalarMatrix deltaEqn ( fvm::ddt(rho_, delta_) + fvm::div(phid, delta_) - fvm::laplacian(ddrhorUAppf, delta_) == - rhoSp_ ); deltaEqn.solve(); if (nonOrth == nNonOrthCorr_) { phiAdd += fvc::interpolate(pp) * fvc::snGrad(delta_) * regionMesh().magSf(); phi_ == deltaEqn.flux(); } } // Bound film thickness by a minimum of zero delta_.max(0.0); // Update U field U_ -= fvc::reconstruct(deltarUAf*phiAdd); // Remove any patch-normal components of velocity U_ -= nHat()*(nHat() & U_); U_.correctBoundaryConditions(); // Update film wall and surface velocities updateSurfaceVelocities(); // Continuity check continuityCheck(); }
2.2.5 Solution Strategy
Equations (1), (3) and (4) represent a system of 3 non-linear partial differential equations with the unknowns 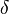 ,
, 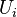 and
and 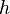 . In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
. In order to solve this system of equations, a splitting method is adopted: The equations are linearised by using quantities from the previous iteration and solved sequentially. The steps performed are the following:
1. Solve continuity equation (1). Here has to be mentioned that the quantity solved for is 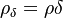 which appears also in the momentum and energy equation.
which appears also in the momentum and energy equation.
2. Solve momentum equation (3)
3. Solve energy equation (4)
4. Solve film thickness equation: The film thickness equation is derived by inserting the discrete momentum equation into the continuity equation.
Steps 2-4 are solved a number of time specified by the user in order to achieve sufficient convergence of the equations. The source code can be found in src/regionModels/surfaceFilmModels/thermoSingleLayer
void thermoSingleLayer::evolveRegion() { if (debug) { InfoInFunction << endl; } // Solve continuity for deltaRho_ solveContinuity(); // Update sub-models to provide updated source contributions updateSubmodels(); // Solve continuity for deltaRho_ solveContinuity(); for (int oCorr=1; oCorr<=nOuterCorr_; oCorr++) { // Explicit pressure source contribution tmp<volScalarField> tpu(this->pu()); // Implicit pressure source coefficient tmp<volScalarField> tpp(this->pp()); // Solve for momentum for U_ tmp<fvVectorMatrix> UEqn = solveMomentum(tpu(), tpp()); // Solve energy for hs_ - also updates thermo solveEnergy(); // Film thickness correction loop for (int corr=1; corr<=nCorr_; corr++) { // Solve thickness for delta_ solveThickness(tpu(), tpp(), UEqn()); } } // Update deltaRho_ with new delta_ deltaRho_ == delta_*rho_; // Update temperature using latest hs_ T_ == T(hs_); }
2.3 Equations Fluid
2.3.1 Mass conservation
The variable-density continuity equation is
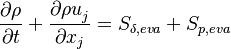 | (11) |
The source terms in the mass conservation equations come from the evaporation of the liquid film 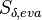 and from
the liquid droplets
and from
the liquid droplets 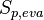 .
.
The source code can be found in rhoEqn.H:
{ fvScalarMatrix rhoEqn ( fvm::ddt(rho) + fvc::div(phi) == parcels.Srho(rho) + surfaceFilm.Srho() + fvOptions(rho) ); rhoEqn.solve(); fvOptions.correct(rho); }
2.3.2 Momentum conservation
The equation of motion are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
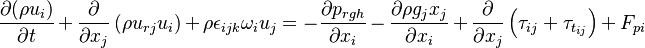 | (12) |
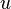 represent the velocity,
represent the velocity, 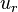 the relative veloicty,
the relative veloicty, 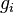 the gravitational acceleration,
the gravitational acceleration, 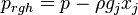 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
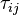 and
and 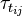 are the viscose and turbulent stresses. Note that since the relative velocity
are the viscose and turbulent stresses. Note that since the relative velocity 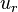 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux  appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
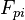 represents the force excreted by the particles on the fluid.
represents the force excreted by the particles on the fluid.
The source code can be found in Ueqn.H:
MRF.correctBoundaryVelocity(U);
fvVectorMatrix UEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence->divDevRhoReff(U)
==
parcels.SU(U)
+ fvOptions(rho, U)
);
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}
2.3.3 Species conservation
In order to account for the chemical reactions occurring between different chemical species a conservation equation for each species k has to be solved:
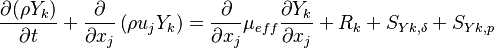 | (13) |
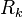 is the reaction rate of the species k and
is the reaction rate of the species k and 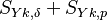 is the contribution to the spices k by the evaporation of the film and the particle respectively.
is the contribution to the spices k by the evaporation of the film and the particle respectively.
The source code can be found in YEEqn.H:
tmp<fv::convectionScheme<scalar>> mvConvection ( fv::convectionScheme<scalar>::New ( mesh, fields, phi, mesh.divScheme("div(phi,Yi_h)") ) ); { combustion->correct(); Qdot = combustion->Qdot(); volScalarField Yt(0.0*Y[0]); forAll(Y, i) { if (i != inertIndex && composition.active(i)) { volScalarField& Yi = Y[i]; fvScalarMatrix YiEqn ( fvm::ddt(rho, Yi) + mvConvection->fvmDiv(phi, Yi) - fvm::laplacian(turbulence->alphaEff(), Yi) == parcels.SYi(i, Yi) + surfaceFilm.Srho(i) + combustion->R(Yi) + fvOptions(rho, Yi) ); YiEqn.relax(); fvOptions.constrain(YiEqn); YiEqn.solve(mesh.solver("Yi")); fvOptions.correct(Yi); Yi.max(0.0); Yt += Yi; } } Y[inertIndex] = scalar(1) - Yt; Y[inertIndex].max(0.0); radiation->correct();
2.3.4 Energy conservation
The derivation of the energy equation (without source terms from the evaporation of the particle 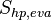 and the liquid film
and the liquid film 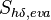 ) can be found in: https://cfd.direct/openfoam/energy-equation/
) can be found in: https://cfd.direct/openfoam/energy-equation/
The total energy of a fluid element can be seen as the sum of kinetic energy 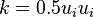 and internal energy
and internal energy  .
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
.
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
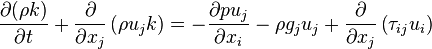 | (14) |
The rate of change of the internal energy  of a fluid element is the heat transferred to this fluid element by diffusion and turbulence
of a fluid element is the heat transferred to this fluid element by diffusion and turbulence 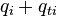 plus the
heat source term
plus the
heat source term  plus the heat source by radiation
plus the heat source by radiation 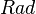 :
:
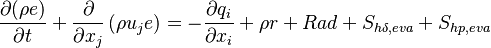 | (15) |
The change rate of the total energy is the sum of the above two equations:
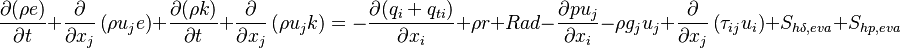 | (16) |
Instead of the internal energy  there is also the option to solve the equation for the enthalpy
there is also the option to solve the equation for the enthalpy 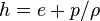 :
:
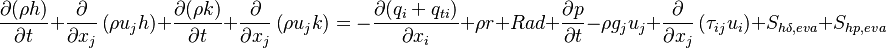 | (17) |
The source code can be found in YEEqn.H:
volScalarField& he = thermo.he();
fvScalarMatrix EEqn
(
fvm::ddt(rho, he) + mvConvection->fvmDiv(phi, he)
+ fvc::ddt(rho, K) + fvc::div(phi, K)
+ (
he.name() == "e"
? fvc::div
(
fvc::absolute(phi/fvc::interpolate(rho), U),
p,
"div(phiv,p)"
)
: -dpdt
)
- fvm::laplacian(turbulence->alphaEff(), he)
==
Qdot
+ radiation->Sh(thermo, he)
+ parcels.Sh(he)
+ surfaceFilm.Sh()
+ fvOptions(rho, he)
);
EEqn.relax();
fvOptions.constrain(EEqn);
EEqn.solve();
fvOptions.correct(he);
thermo.correct();
Info<< "min/max(T) = "
<< min(T).value() << ", " << max(T).value() << endl;
2.3.5 Pressure equation
As most of the solvers of OpenFOAM also fireFoam is a pressure based solver. In this class of solvers, the discrete momentum equation (which contains also the pressure gradient) is used to obtain a semi discrete equation for the velocity at the cell centre. This velocity is cast into the continuity equation in order to obtain an equation for the pressure which satisfies the mass conservation and by construction also the momentum equation. It has also to be mentioned, that the pressure equation which is solved, is only valid for law Mach number flows, i.e., it is assumed that the density has only a weak dependency from the pressure. Large temperature variation are however allowed (see the difference to the pressure equation solved in https://openfoamwiki.net/index.php/ChtMultiRegionFoam).
Starting point for the derivation of the pressure equation is the discrete continuity equation after integrating over the control volume:
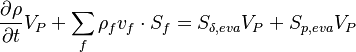 | (18) |
The subscript f denotes the the quantities are evaluated at the cell faces. The semi discrete momentum equation reads:
![\bold{A_P U_P} - \bold {H[U]} = - \nabla p_{rgh,P} - g \cdot x \nabla \rho](/images/math/1/d/b/1db5afd48eed9f3b7e872a3b3f58aaf6.png) | (19) |
and after rearranging with respect to the velocity at the cell centre 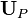 :
:
![\bold{ U_P} = \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho}{\bold A_P}](/images/math/a/c/2/ac2c0b09ce13348e276a799ac7dfdf74.png) | (20) |
and
are the contribution of the off diagonal elements of the matrix and the diagonal elements of the matrix, respectively.
The above equation can be inserted into the continuity equation:
![\frac{ \partial \rho}{\partial t} V_P + \sum_f \rho_f \left ( \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho}{\bold A_P} \right )_f \cdot S_f = S_{\delta,eva}V_P + S_{p,eva}V_P](/images/math/2/2/4/224f0fd6b344158c7d56bf102aa02aa0.png) | (21) |
Since the above equation still contains the density a relation between the density and the pressure is required. In the most general form it can be expressed as:
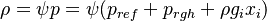 | (22) |
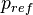 is the reference pressure.
is the reference pressure.
If we insert equation (22) into equation (21) we get a non-linear equation for the pressure when evaluating the divergence (the second term in equation (21)). However, if we assume only a week dependence of the density from the pressure, the density at the previous iteration 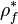 can be taken as a reasonable approximation of the
density at the current iteration step
can be taken as a reasonable approximation of the
density at the current iteration step 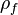 . Since we can still have a strong variation of the density with time (in turbulent combustion the temperature is highly in-stationary and hence also the density varies considerably with time) the temporal derivatives have to be kept. The resulting equation reads:
. Since we can still have a strong variation of the density with time (in turbulent combustion the temperature is highly in-stationary and hence also the density varies considerably with time) the temporal derivatives have to be kept. The resulting equation reads:
![\frac{ \partial \psi ( p_{ref} + p_{rgh} + \rho^* g_i x_i )}{\partial t} V_P + \sum_f \rho_f^* \left ( \frac{ \bold {H[U]}}{\bold A_P} - \frac{\nabla p_{rgh,P}}{\bold A_P} - \frac{ g \cdot x \nabla \rho^*}{\bold A_P} \right )_f \cdot S_f = S_{\delta,eva}V_P + S_{p,eva}V_P](/images/math/4/2/f/42fcc28e9376fa5f554c8c92fad2b295.png) | (23) |
The source code can be found in pEqn.H:
rho = thermo.rho(); volScalarField rAU(1.0/UEqn.A()); surfaceScalarField rhorAUf("rhorAUf", fvc::interpolate(rho*rAU)); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); surfaceScalarField phig("phig", -rhorAUf*ghf*fvc::snGrad(rho)*mesh.magSf()); surfaceScalarField phiHbyA ( "phiHbyA", ( fvc::flux(rho*HbyA) + MRF.zeroFilter(rhorAUf*fvc::ddtCorr(rho, U, phi)) ) + phig ); MRF.makeRelative(fvc::interpolate(rho), phiHbyA); // Update the pressure BCs to ensure flux consistency constrainPressure(p_rgh, rho, U, phiHbyA, rhorAUf, MRF); while (pimple.correctNonOrthogonal()) { fvScalarMatrix p_rghEqn ( fvm::ddt(psi, p_rgh) + fvc::ddt(psi, rho)*gh + fvc::ddt(psi)*pRef + fvc::div(phiHbyA) - fvm::laplacian(rhorAUf, p_rgh) == parcels.Srho() + surfaceFilm.Srho() + fvOptions(psi, p_rgh, rho.name()) ); p_rghEqn.solve(mesh.solver(p_rgh.select(pimple.finalInnerIter()))); if (pimple.finalNonOrthogonalIter()) { phi = phiHbyA + p_rghEqn.flux(); U = HbyA + rAU*fvc::reconstruct((p_rghEqn.flux() + phig)/rhorAUf); U.correctBoundaryConditions(); fvOptions.correct(U); } } p = p_rgh + rho*gh + pRef; #include "rhoEqn.H" #include "compressibleContinuityErrs.H" K = 0.5*magSqr(U); if (thermo.dpdt()) { dpdt = fvc::ddt(p); }
2.4 Pyrolysis
Cite error: <ref> tags exist, but no <references/> tag was found