(Fixed fluxes replaced dot with \cdot, removed OpenCFD [M[U]] notation) |
m (→Momentum) |
||
| Line 65: | Line 65: | ||
</center> | </center> | ||
| − | or in terms of the flux which | + | or in terms of the flux <math>\mathbf{\Phi}</math> which is discretised at cell faces to <math>\phi</math> (unlike most other quantities which are discretised to cell centres), |
<center> | <center> | ||
Latest revision as of 04:38, 18 September 2009
Contents
1 Overview
The buoyantPisoFoam solver is suitable for unsteady, compressible flow and includes the gravitational body force on the fluid. The Richardson number is a dimensionless measure of the importance of buoyancy in a flow.
2 Nomenclature
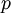
|
p | pressure |
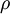
|
rho | density |
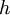
|
h | enthalpy |
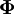
|
mass flux, 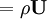
| |
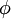
|
phi | mass flux through faces, 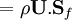
|
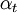
|
alphaEff | effective turbulent thermal diffusivity |
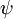
|
psi | compressibility 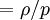
|
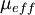
|
muEff | effective viscosity 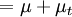
|
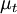
|
turbulent viscosity | |
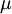
|
mu | laminar molecular viscosity |
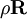
|
divRhoR | Reynolds stresses 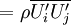
|
3 Momentum
The primary Navier Stokes equation is for the transport of momentum with sources and sinks.
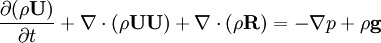
or in terms of the flux 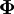 which is discretised at cell faces to
which is discretised at cell faces to  (unlike most other quantities which are discretised to cell centres),
(unlike most other quantities which are discretised to cell centres),
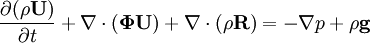
|
| File: OpenFOAM-1.6/applications/solvers/heatTransfer/buoyantPisoFoam/UEqn.H |
fvVectorMatrix UEqn
(
fvm::ddt(rho, U)
+ fvm::div(phi, U)
+ turbulence->divDevRhoR(U)
);
UEqn.relax();
solve(UEqn == -fvc::grad(p) - fvc::grad(rho)*gh);
|
We note that the mass flux is on hard-wired linear interpolation from cell centres to faces,
| File: OpenFOAM-1.6.x/src/finiteVolume/cfdTools/compressible/compressibleCreatePhi.H |
surfaceScalarField phi
(
IOobject
(
"phi",
runTime.timeName(),
mesh,
IOobject::READ_IF_PRESENT,
IOobject::AUTO_WRITE
),
linearInterpolate(rho*U) & mesh.Sf()
);
|
4 Mass
Conservation of mass provides a relation between the local rate of change of density and the degree to which the local mass flux is acting as a source or sink.
|
| File: OpenFOAM-1.6/src/finiteVolume/cfdTools/compressible/rhoEqn.H |
{
solve(fvm::ddt(rho) + fvc::div(phi));
}
|
5 Energy
Actually the more general concept of enthalpy is used. This is more relevant for gases and chemical reactions because it accounts for internal energy and the work done by the system, or in other words kinetic and potential energy.
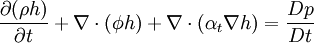
|
| File: applications/solvers/heatTransfer/buoyantPisoFoam/hEqn.H |
{
solve
(
fvm::ddt(rho, h)
+ fvm::div(phi, h)
- fvm::laplacian(turbulence->alphaEff(), h)
==
DpDt
);
hEqn.relax();
hEqn.solve();
thermo.correct();
}
|
6 Turbulence
6.1 Momentum source
The Reynolds stresses are estimated [1] via the tensor
![\begin{align}
\mathbf{R} & = \frac{2}{3} \mathbf{I} k - 2 \frac{\mu_{t} }{\rho} \mathrm{dev} \left[ \mathrm{symm} \left( \nabla \mathbf{U} \right) \right ] \\
& = \frac{2}{3} \mathbf{I} k - 2 \frac{\mu_{t}}{\rho} \left( \mathrm{symm} \left( \nabla \mathbf{U} \right) - \frac{1}{3} \mathrm{ tr } \left( \mathrm{symm} \left( \nabla \mathbf{U} \right) \right) \mathbf{I} \right) \\
& = \frac{2}{3} \mathbf{I} k - 2 \frac{\mu_{t}}{\rho} \left( \frac{1}{2} \left( \nabla \mathbf{U} + ( \nabla \mathbf{U} )^{T} \right) - \frac{1}{3} \mathrm{tr} \left( \nabla \mathbf{U} \right) \mathbf{I} \right) \\
\end{align}](/images/math/6/8/0/680b521d128c63068ac9063f506d608a.png)
because the trace of the symmetric component of a tensor is just the trace of the original tensor,
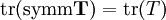
| File: OpenFOAM-1.6/src/turbulenceModels/compressible/RAS/kOmegaSST/kOmegaSST.C |
273 tmp<volSymmTensorField> kOmegaSST::R() const
274 {
275 return tmp<volSymmTensorField>
276 (
277 new volSymmTensorField
278 (
279 IOobject
280 (
281 "R",
282 runTime_.timeName(),
283 mesh_,
284 IOobject::NO_READ,
285 IOobject::NO_WRITE
286 ),
287 ((2.0/3.0)*I)*k_ - (mut_/rho_)*dev(twoSymm(fvc::grad(U_))),
288 k_.boundaryField().types()
289 )
290 );
291 }
|
The divergence of the product appearing in the momentum equations is estimated as
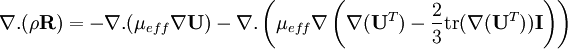
| File: OpenFOAM-1.6/src/turbulenceModels/compressible/RAS/kOmegaSST/kOmegaSST.C |
314 tmp<fvVectorMatrix> kOmegaSST::divDevRhoReff(volVectorField& U) const
315 {
316 return
317 (
318 - fvm::laplacian(muEff(), U) - fvc::div(muEff()*dev2(fvc::grad(U)().T()))
319 );
320 }
|
For reference,
![\mathrm{ grad \ } \mathbf{ U } = \nabla \mathbf{ U } = \left[ \begin{array}{ccc}
\dfrac{\partial U_{x}}{\partial x} & \dfrac{\partial U_{y}}{\partial x} & \dfrac{\partial U_{z}}{\partial x} \\
\\
\dfrac{\partial U_{x}}{\partial y} & \dfrac{\partial U_{y}}{\partial y} & \dfrac{\partial U_{z}}{\partial y} \\
\\
\dfrac{\partial U_{x}}{\partial z} & \dfrac{\partial U_{y}}{\partial z} & \dfrac{\partial U_{z}}{\partial z} \\
\end{array} \right]](/images/math/6/b/b/6bba2f60ddfa80785a7ebb32793d5107.png)
7 PISO
The non linearity of the convection term of the momentum equation requires an iterative solution technique if we do not wish to be limited to small time steps. But while the momentum equation provides a way to find the velocity in terms of the pressure gradient, we need some way to determine the pressure as we iterate. In the Pressure-Implicit Split-Operator (PISO) approach, we formulate a linear relationship between the pressure gradient and the velocity in order to obtain a prediction of the velocity (which violates mass conservation), then apply the mass conservation requirement in order to obtain a pressure field that is mass conservative so that it can be fed back to obtain a corrected velocity field. At the same time, we correct for face skewness by updating the mass fluxes at cell faces with the new pressure field.
The momentum equation is discretised at  discrete locations to obtain
discrete locations to obtain
or
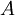 and
and 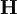 are then reconstituted to make
are then reconstituted to make 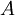 into a diagonal matrix with the "offcuts" placed into the square matrix
into a diagonal matrix with the "offcuts" placed into the square matrix 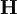
Multiplying both sides by the inverse of 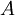 yields the momentum corrector equation
yields the momentum corrector equation
Applying mass conservation, we obtain the pressure corrector equation
This is solved to provide a pressure field inserted into a flux corrector equation
7.1 Algorithm
| Step | Equations | Code | Comments | |
|---|---|---|---|---|
| 1 | Accept 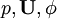 , and require , and require 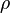
|
while (runTime.loop())
{
...
}
|
The "old" values go into the loop, either initialised in createFields.H or provided by previous time step. | |
| 2 | 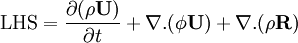
|
fvVectorMatrix UEqn
(
fvm::ddt(rho, U)
+ fvm::div(phi, U)
+ turbulence->divDevRhoR(U)
);
|
Assemble the LHS of the momentum equation and discretise it into matrix form using the vector calculus schemes in fvSchemes. | |
| 3 | 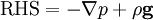
|
UEqn.relax();
if (momentumPredictor)
{
solve
(
UEqn
==
fvc::reconstruct
(
fvc::interpolate(rho)*(g & mesh.Sf())
- fvc::snGrad(p)*mesh.magSf()
)
);
}
|
This predictor step uses the old pressure and so while momentum conservation is satisfied, mass conservation is normally not satisfied. In some cases (e.g. low Re flow), switching off this momentum predictor via the switch in fvSolution can improve solution speed. Notice that the LHS is formulated in implicit (matrix) terms (i.e. fvm:: while the RHS terms are explicit (i.e. fvc::). The equation is therefore solved implicitely. |
7.2 References
- ↑ Ferziger, J. H. and Peric, M., Computational Methods for Fluid Dynamics, 3rd Edition, Springer, 2002, Eqn. 9.40
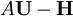
![\left[ \begin{array}{cccc}
A_{11} & A_{12} & \ldots & A_{1N} \\
A_{21} & A_{22} & \ldots & A_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
A_{N1} & A_{N2} & \ldots & A_{NN} \\
\end{array} \right]
\left[ \begin{array}{c}
\mathbf{U}_{1} \\
\mathbf{U}_{2} \\
\vdots \\
\mathbf{U}_{N} \\
\end{array} \right] =
\left[ \begin{array}{c}
H_{1} \\
H_{2} \\
\vdots \\
H_{N} \\
\end{array} \right]](/images/math/a/a/5/aa54d478ab48d3a2eac336e057f039b8.png)
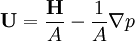
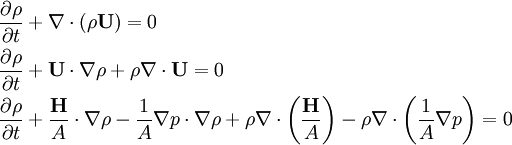
![\begin{align}
\phi & = \mathbf{S}_{f} . \mathbf{U}_{f} \\
& = \mathbf{S}_{f} \cdot \left[ \left( \frac{\mathbf{H}}{A} \right)_{f} - \left( \frac{1}{A} \right)_{f} ( \nabla p )_{f} \right] \\
\end{align}](/images/math/6/9/f/69ff10bce6ec396d69eec1e641afc8d5.png)