DarcyForchheimer
Contents
1 Darcy Fochheimer Explanation
The Darcy Forchheimer model allows us to simply add a porosity zone into our fluid domain without any expense. In order to use the model, you have to put a fvOptions file into the constant folder including the following content (OpenFOAM-v6):
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: dev |
| \\ / A nd | Web: www.OpenFOAM.org |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
location "constant";
object fvOptions;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
porosity1
{
type explicitPorositySource;
explicitPorositySourceCoeffs
{
selectionMode cellZone;
cellZone cat1;
type DarcyForchheimer;
f (0.63 1e6 1e6);
d (80.25 1e6 1e6);
coordinateSystem
{
type cartesian;
origin (0 0 0);
coordinateRotation
{
type axesRotation;
e1 (1 0 0);
e2 (0 1 0);
}
}
}
}
2 The Darcy-Forchheimer Equation
The Darcy Forchheimer acts in the momentum equation as a sink term 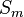 . Considering the momentum equation, it follows:
. Considering the momentum equation, it follows:
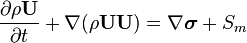
Here, the Cauchy stress tensor 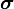 is not split into its deviatoric and hydrostatic part (shear-rate and pressure). The main important term is the source term
is not split into its deviatoric and hydrostatic part (shear-rate and pressure). The main important term is the source term 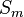 which is given as:
which is given as:
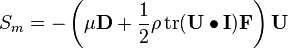
While the coefficients 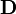 and
and 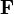 have to be specified in the fvOptions file (see code above). The souce term
have to be specified in the fvOptions file (see code above). The souce term 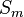 represents a sink as the sign is negative.
represents a sink as the sign is negative.
2.1 Calculate the Coefficients
In order to use the Darcy-Forchheimer equation, the coefficients D and F have to be estimated. For porous media we need the velocity dependent pressure p(u) function of the porous media. E.g., the above equation for 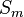 can be written as:
can be written as:
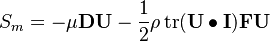
As the source term 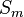 can be expressed as a pressure gradient it follows
can be expressed as a pressure gradient it follows 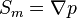 . Therefore, we can write:
. Therefore, we can write:
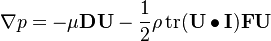
While switching to the Cartesian coordinate system, we can achieve something similar to:
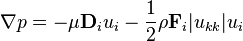
If we know the velocity dependent pressure we can calculate a polynomial function such as:
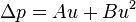
Comparing both equations, we can say:
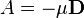
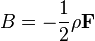
Therefore, knowing the velocity dependent pressure values, we can calculate A and B and thus, the coefficients 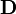 and
and 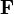 can be recalculated. It should be clear, that the vectors
can be recalculated. It should be clear, that the vectors 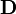 and
and 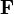 can be direction dependent.
can be direction dependent.
2.2 Porous Media such as Honeycombs
Porous media that only have one flow direction, e.g., honeycombs, has to block two directions of the flow. To achieve that, we can set high values for 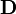 and
and 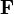 .
.