OpenFOAM guide/The PISO algorithm in OpenFOAM
1 The PISO algorithm
The PISO (Pressure Implicit with Splitting of Operators) is an efficient method to solve the Navier-Stokes equations in unsteady problems. The main differences from the SIMPLE algorithm are the following:
- No under-relaxation is applied.
- The momentum corrector step is performed more than once.
The algorithm can be summed up as follows:
- Set the boundary conditions.
- Solve the discretized momentum equation to compute an intermediate velocity field.
- Compute the mass fluxes at the cells faces.
- Solve the pressure equation.
- Correct the mass fluxes at the cell faces.
- Correct the velocities on the basis of the new pressure field.
- Update the boundary conditions.
- Repeat from 3 for the prescribed number of times.
- Increase the time step and repeat from 1.
As already seen for the SIMPLE algorithm, the steps 4 and 5 can be repeated for a prescribed number of time to correct for non-orthogonality.
2 Implementation of the PISO algorithm in OpenFOAM
The PISO algorithm is implemented in OpenFOAM as follows (Details can be found in the icoFoam standard solver provided with OpenFOAM):
- Define the equation for U
fvVectorMatrix UEqn ( fvm::ddt(U) + fvm::div(phi, U) - fvm::laplacian(nu, U) );
- Solve the momentum predictor
solve (UEqn == -fvc::grad(p));
- Calculate the
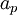 coefficient and calculate U
coefficient and calculate U
volScalarField rUA = 1.0/UEqn().A(); U = rUA*UEqn().H();
- Calculate the flux
phi = (fvc::interpolate(U) & mesh.Sf()) + fvc::ddtPhiCorr(rUA, U, phi); adjustPhi(phi, U, p);
- Define and solve the pressure equation and repeat for the prescribed number of non-orthogonal corrector steps
fvScalarMatrix pEqn ( fvm::laplacian(rUA, p) == fvc::div(phi) ); pEqn.setReference(pRefCell, pRefValue); pEqn.solve();
- Correct the flux
if (nonOrth == nNonOrthCorr) { phi -= pEqn.flux(); }
- Calculate continuity errors
# include "continuityErrs.H"
- Perform the momentum corrector step
U -= rUA*fvc::grad(p); U.correctBoundaryConditions();
- Repeat from the calculation of
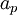 for the prescribed number of PISO corrector steps.
for the prescribed number of PISO corrector steps.
3 References
J. H. Ferziger, M. Peric, Computational Methods for Fluid Dynamics, Springer, 3rd Ed., 2001.
H. Jasak, Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows, Ph.D. Thesis, Imperial College, London, 1996.